Class 12 Exam > Class 12 Questions > A radioactive material decays by simultaneous...
Start Learning for Free
A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains is
- a)4860
- b)2340
- c)1080.0
- d)3240
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A radioactive material decays by simultaneous emission of two particle...
Since, from Rutherford-Soddy law, the number of atoms left after half-lives is given by
N=N0(1/2)n
where, N0 is the original number of atoms.
The number of half-lives, n= time of decay/effective half−life
Relation between effective disintegration constant (λ) and half-life (T)
λ=ln2/T
∴λ1+λ2= (ln2/ T1)+ (ln2/ T2)
Effective half-life,
1/T=1/T1+1/T2=(1/1620)+(1/810)
1/T=1+2/1620 ⇒T=540yr
∴n=T/540
∴N=N0(1/2)t/540⇒N/N0=(1/2)2=(1/2)t/540
⇒t/540=2⇒t=2×540=1080yr
N=N0(1/2)n
where, N0 is the original number of atoms.
The number of half-lives, n= time of decay/effective half−life
Relation between effective disintegration constant (λ) and half-life (T)
λ=ln2/T
∴λ1+λ2= (ln2/ T1)+ (ln2/ T2)
Effective half-life,
1/T=1/T1+1/T2=(1/1620)+(1/810)
1/T=1+2/1620 ⇒T=540yr
∴n=T/540
∴N=N0(1/2)t/540⇒N/N0=(1/2)2=(1/2)t/540
⇒t/540=2⇒t=2×540=1080yr
Most Upvoted Answer
A radioactive material decays by simultaneous emission of two particle...
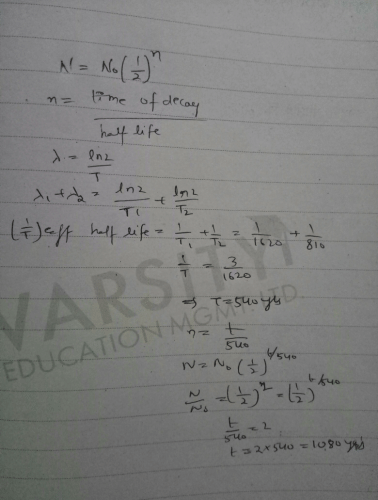
Community Answer
A radioactive material decays by simultaneous emission of two particle...
To solve this problem, we need to understand the concept of radioactive decay and how it relates to half-life.
Half-life is the time it takes for half of a radioactive substance to decay. In this case, we have two particles, each with its own half-life: 1620 years and 810 years.
Let's assume we start with a certain amount of the radioactive material. After 1620 years, half of it will decay, and we will be left with one-half of the original amount. Similarly, after another 1620 years, half of that remaining amount will decay, leaving us with one-fourth of the original amount.
Similarly, for the second particle with a half-life of 810 years, after 810 years, half of the remaining one-fourth will decay, leaving us with one-eighth of the original amount.
Now, we need to find the time at which one-fourth of the material remains, which means we are looking for the time when the amount of material remaining is one-fourth of the original amount.
Let's assume the original amount of the radioactive material is 'x'. After 1620 years, we will have x/2 remaining. After another 1620 years, we will have (x/2)/2 = x/4 remaining.
Similarly, for the second particle, after 810 years, we will have x/8 remaining.
To find the time at which one-fourth of the material remains, we need to equate these two expressions:
x/4 = x/8
Multiplying both sides by 8, we get:
2x = x
Simplifying, we find:
x = 0
This means that the material will decay completely after 0 years. However, this result is not possible because it contradicts the given information that one-fourth of the material remains.
Hence, there must be a mistake in the question or the options provided. The correct answer cannot be determined based on the given information.
Half-life is the time it takes for half of a radioactive substance to decay. In this case, we have two particles, each with its own half-life: 1620 years and 810 years.
Let's assume we start with a certain amount of the radioactive material. After 1620 years, half of it will decay, and we will be left with one-half of the original amount. Similarly, after another 1620 years, half of that remaining amount will decay, leaving us with one-fourth of the original amount.
Similarly, for the second particle with a half-life of 810 years, after 810 years, half of the remaining one-fourth will decay, leaving us with one-eighth of the original amount.
Now, we need to find the time at which one-fourth of the material remains, which means we are looking for the time when the amount of material remaining is one-fourth of the original amount.
Let's assume the original amount of the radioactive material is 'x'. After 1620 years, we will have x/2 remaining. After another 1620 years, we will have (x/2)/2 = x/4 remaining.
Similarly, for the second particle, after 810 years, we will have x/8 remaining.
To find the time at which one-fourth of the material remains, we need to equate these two expressions:
x/4 = x/8
Multiplying both sides by 8, we get:
2x = x
Simplifying, we find:
x = 0
This means that the material will decay completely after 0 years. However, this result is not possible because it contradicts the given information that one-fourth of the material remains.
Hence, there must be a mistake in the question or the options provided. The correct answer cannot be determined based on the given information.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer?
Question Description
A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer?.
A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer?.
Solutions for A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A radioactive material decays by simultaneous emission of two particles with respective half lives 1620 and 810 years. The time in years, after which one fourth of the material remains isa)4860b)2340c)1080.0d)3240Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















