JEE Exam > JEE Questions > In case of a projectile, the angular momentum...
Start Learning for Free
In case of a projectile, the angular momentum is minimum
- a)at some location other than those mentioned above
- b)at the starting point
- c)at the highest point
- d)on return to the ground
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
In case of a projectile, the angular momentum is minimuma)at some loca...
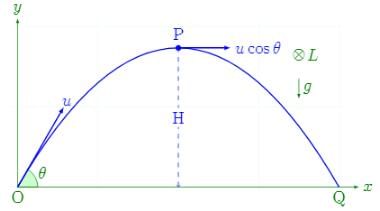
At the starting point of the projectile, the perpendicular distance from the point of rotation is zero as it's on the ground itself. Since one factor of the product is zero, the angular momentum at the starting point will be zero too.
Free Test
FREE
| Start Free Test |
Community Answer
In case of a projectile, the angular momentum is minimuma)at some loca...
Understanding Angular Momentum in Projectile Motion
In projectile motion, angular momentum is an essential concept that relates to the motion of the object concerning a point, usually the origin or a reference point. The angular momentum of a projectile is influenced by its velocity and the distance from the reference point.
Angular Momentum at Different Points
- Starting Point: At the moment the projectile is launched, it has a certain velocity and is at a defined distance from the reference point. The angular momentum is calculated using the formula L = r × p, where r is the distance from the reference point and p is the linear momentum (mass × velocity).
- Highest Point: At the peak of its trajectory, the vertical component of the projectile's velocity is zero. However, it still has horizontal velocity. While the angular momentum here is not minimum, it is essential to note that it is still influenced by the horizontal distance from the reference point.
- Return to the Ground: When the projectile returns to the ground, it has a similar distance from the reference point as it had at launch, therefore the angular momentum is nearly similar to that at the starting point.
Why Minimum at Starting Point?
- When the projectile is launched, it has the most significant distance from the reference point given the initial height. As it travels upwards and then downwards, the distance decreases and then increases again, but it is always zero at the starting point regarding the vertical component.
- The minimum angular momentum occurs when the reference point is at the launch point, as any deviation from this point in terms of height or horizontal distance will yield a greater angular momentum due to the nature of the r × p relationship.
In conclusion, the correct answer is option 'B', as the angular momentum is minimum at the starting point.
In projectile motion, angular momentum is an essential concept that relates to the motion of the object concerning a point, usually the origin or a reference point. The angular momentum of a projectile is influenced by its velocity and the distance from the reference point.
Angular Momentum at Different Points
- Starting Point: At the moment the projectile is launched, it has a certain velocity and is at a defined distance from the reference point. The angular momentum is calculated using the formula L = r × p, where r is the distance from the reference point and p is the linear momentum (mass × velocity).
- Highest Point: At the peak of its trajectory, the vertical component of the projectile's velocity is zero. However, it still has horizontal velocity. While the angular momentum here is not minimum, it is essential to note that it is still influenced by the horizontal distance from the reference point.
- Return to the Ground: When the projectile returns to the ground, it has a similar distance from the reference point as it had at launch, therefore the angular momentum is nearly similar to that at the starting point.
Why Minimum at Starting Point?
- When the projectile is launched, it has the most significant distance from the reference point given the initial height. As it travels upwards and then downwards, the distance decreases and then increases again, but it is always zero at the starting point regarding the vertical component.
- The minimum angular momentum occurs when the reference point is at the launch point, as any deviation from this point in terms of height or horizontal distance will yield a greater angular momentum due to the nature of the r × p relationship.
In conclusion, the correct answer is option 'B', as the angular momentum is minimum at the starting point.

|
Explore Courses for JEE exam
|

|
Question Description
In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer?.
In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer?.
Solutions for In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In case of a projectile, the angular momentum is minimuma)at some location other than those mentioned aboveb)at the starting pointc)atthe highest pointd)on return to the groundCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















