Class 9 Exam > Class 9 Questions > In an equilateral triangle ABC,AD is the alti...
Start Learning for Free
In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2
Most Upvoted Answer
In an equilateral triangle ABC,AD is the altitude drawn from A to side...
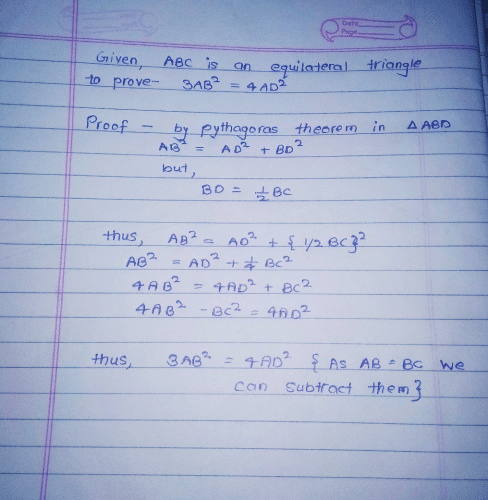
Community Answer
In an equilateral triangle ABC,AD is the altitude drawn from A to side...
Proof:
To prove that 3AB^2 = 4AD^2 in an equilateral triangle ABC, where AD is the altitude drawn from A to side BC, we can use the Pythagorean theorem and the properties of an equilateral triangle.
Properties of an equilateral triangle:
- All sides of an equilateral triangle are equal.
- All angles of an equilateral triangle are equal and measure 60 degrees.
- The altitude of an equilateral triangle bisects the base.
Proof:
We start by drawing the equilateral triangle ABC and the altitude AD from A to side BC.
Step 1: Label the triangle and the given information.
Let's label the triangle as ABC and the altitude as AD.
Step 2: Use the property that the altitude of an equilateral triangle bisects the base.
Since AD is the altitude of the equilateral triangle ABC, it bisects the base BC at point E.
Step 3: Use the property that all angles of an equilateral triangle measure 60 degrees.
Since ABC is an equilateral triangle, angle BAC measures 60 degrees.
Step 4: Use the Pythagorean theorem.
In right triangle ADE, we can apply the Pythagorean theorem:
AD^2 + DE^2 = AE^2
Step 5: Determine the lengths of the sides and the altitude.
Since ABC is an equilateral triangle, all sides are equal, so AB = BC = AC.
Since AD is the altitude, it is perpendicular to BC, so angle ADE is a right angle.
Based on the properties of an equilateral triangle, we know that AD bisects BC at point E, so BE = CE = BC/2.
Step 6: Calculate the lengths of AE and DE.
Using the properties of an equilateral triangle, we can determine the lengths of AE and DE.
Since ABC is an equilateral triangle, triangle ABE is a 30-60-90 right triangle.
In a 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg.
Therefore, AE = 2 * DE.
Step 7: Substitute the lengths into the Pythagorean theorem equation.
Substituting the lengths into the equation AD^2 + DE^2 = AE^2, we have:
AD^2 + DE^2 = (2 * DE)^2
AD^2 + DE^2 = 4 * DE^2
Step 8: Simplify the equation.
Simplifying the equation, we have:
AD^2 = 3 * DE^2
Step 9: Substitute the lengths of DE and BC.
Since DE = BC/2, we can substitute this length into the equation:
AD^2 = 3 * (BC/2)^2
AD^2 = 3 * (BC^2/4)
AD^2 = 3 * BC^2/4
Step 10: Use the property that all sides of an equilateral triangle are equal.
Since AB = BC = AC, we can substitute AB for BC in the equation:
AD^2 = 3 * AB^
To prove that 3AB^2 = 4AD^2 in an equilateral triangle ABC, where AD is the altitude drawn from A to side BC, we can use the Pythagorean theorem and the properties of an equilateral triangle.
Properties of an equilateral triangle:
- All sides of an equilateral triangle are equal.
- All angles of an equilateral triangle are equal and measure 60 degrees.
- The altitude of an equilateral triangle bisects the base.
Proof:
We start by drawing the equilateral triangle ABC and the altitude AD from A to side BC.
Step 1: Label the triangle and the given information.
Let's label the triangle as ABC and the altitude as AD.
Step 2: Use the property that the altitude of an equilateral triangle bisects the base.
Since AD is the altitude of the equilateral triangle ABC, it bisects the base BC at point E.
Step 3: Use the property that all angles of an equilateral triangle measure 60 degrees.
Since ABC is an equilateral triangle, angle BAC measures 60 degrees.
Step 4: Use the Pythagorean theorem.
In right triangle ADE, we can apply the Pythagorean theorem:
AD^2 + DE^2 = AE^2
Step 5: Determine the lengths of the sides and the altitude.
Since ABC is an equilateral triangle, all sides are equal, so AB = BC = AC.
Since AD is the altitude, it is perpendicular to BC, so angle ADE is a right angle.
Based on the properties of an equilateral triangle, we know that AD bisects BC at point E, so BE = CE = BC/2.
Step 6: Calculate the lengths of AE and DE.
Using the properties of an equilateral triangle, we can determine the lengths of AE and DE.
Since ABC is an equilateral triangle, triangle ABE is a 30-60-90 right triangle.
In a 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg.
Therefore, AE = 2 * DE.
Step 7: Substitute the lengths into the Pythagorean theorem equation.
Substituting the lengths into the equation AD^2 + DE^2 = AE^2, we have:
AD^2 + DE^2 = (2 * DE)^2
AD^2 + DE^2 = 4 * DE^2
Step 8: Simplify the equation.
Simplifying the equation, we have:
AD^2 = 3 * DE^2
Step 9: Substitute the lengths of DE and BC.
Since DE = BC/2, we can substitute this length into the equation:
AD^2 = 3 * (BC/2)^2
AD^2 = 3 * (BC^2/4)
AD^2 = 3 * BC^2/4
Step 10: Use the property that all sides of an equilateral triangle are equal.
Since AB = BC = AC, we can substitute AB for BC in the equation:
AD^2 = 3 * AB^
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2
Question Description
In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2.
In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2.
Solutions for In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 defined & explained in the simplest way possible. Besides giving the explanation of
In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2, a detailed solution for In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 has been provided alongside types of In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 theory, EduRev gives you an
ample number of questions to practice In an equilateral triangle ABC,AD is the altitude drawn from A to side BC. Prove that 3AB^2=4AD^2 tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























