JEE Exam > JEE Questions > If then I is equal toa)b)c)d)Correct answer ...
Start Learning for Free
If 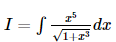 then I is equal to
then I is equal to
- a)
- b)
- c)
- d)
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you ex...
Write x^5 as x³. x² and take x³ as t. Now x² will become dt/3.Substitute in x³ and x² and then solve the foll.
Free Test
FREE
| Start Free Test |
Community Answer
If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you ex...
Step 1: Try a substitution
Let v = √(1 + x³)
Then,
v² = 1 + x³ ⇒ x³ = v² - 1
v² = 1 + x³ ⇒ x³ = v² - 1
Now differentiate both sides of v² = 1 + x³:
2v dv = 3x² dx ⇒ x² dx = (2v / 3) dv
2v dv = 3x² dx ⇒ x² dx = (2v / 3) dv
Now rewrite the integral:
I = ∫ (x³ / √(1 + x³)) dx = ∫ [(v² - 1) / v] * (2v / 3) dv
Simplify:
I = (2 / 3) ∫ (v² - 1) dv
I = (2 / 3) ∫ (v² - 1) dv
Step 2: Integrate
I = (2 / 3) ∫ (v² - 1) dv = (2 / 3) * [ (v³ / 3) - v ] + C
I = (2 / 9) v³ - (2 / 3) v + C
Now substitute back v = √(1 + x³):
I = (2 / 9) * (1 + x³)3/2 - (2 / 3) * (1 + x³)1/2 + C
Final Answer:
I = (2 / 9)(1 + x³)3/2 - (2 / 3)(1 + x³)1/2 + C
This matches option d, so the correct answer is:
Option d)

|
Explore Courses for JEE exam
|

|
Question Description
If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer?.
If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer?.
Solutions for If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer?, a detailed solution for If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If then I is equal toa)b)c)d)Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















