Class 11 Exam > Class 11 Questions > The length of a second’s pendulum decre...
Start Learning for Free
The length of a second’s pendulum decreases by 0.1percent, then the clock
- a)Loses 43.2 seconds per day
- b)Loses 13.5 seconds per day
- c)Loses 7 seconds per day
- d)Gains 43.2 seconds per day
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The length of a second’s pendulum decreases by 0.1percent, then ...
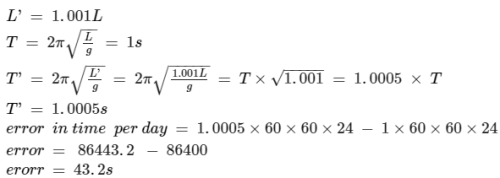
Most Upvoted Answer
The length of a second’s pendulum decreases by 0.1percent, then ...
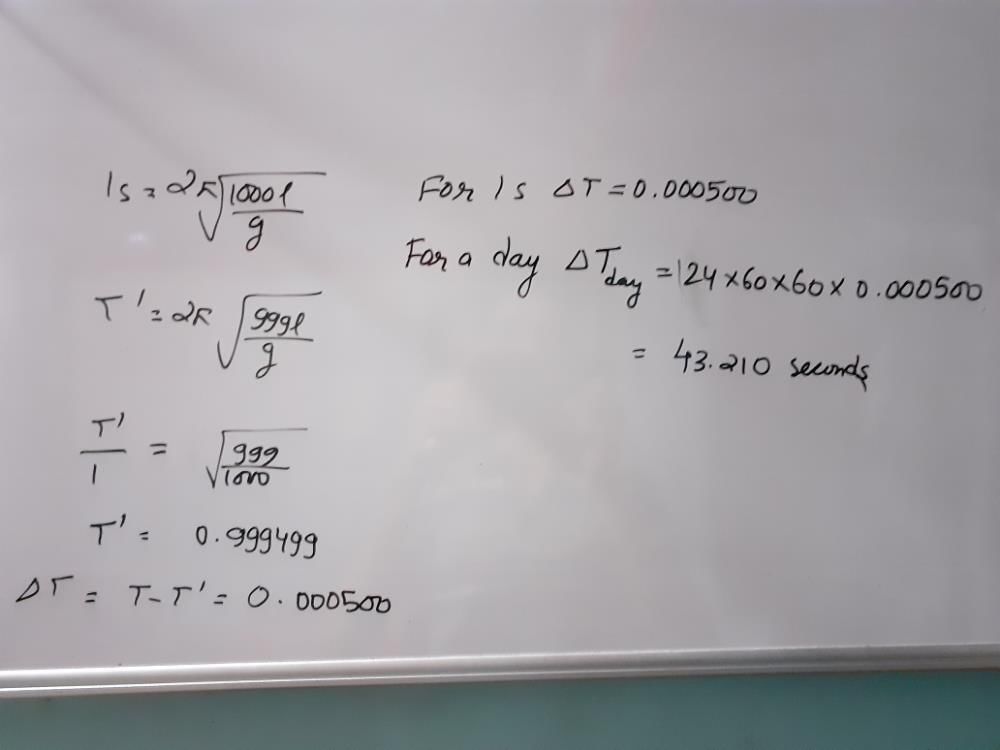
Free Test
FREE
| Start Free Test |
Community Answer
The length of a second’s pendulum decreases by 0.1percent, then ...
The length of a seconds pendulum refers to the length of a pendulum that takes one second to complete a full swing. Let's assume the original length of the seconds pendulum is L.
Given:
The length of the seconds pendulum decreases by 0.1 percent.
To find:
The change in the time on the clock.
Formula:
The time period of a pendulum is given by the formula:
T = 2π√(L/g)
where T is the time period, L is the length of the pendulum, and g is the acceleration due to gravity.
Analysis:
When the length of the pendulum decreases, the time period also decreases. This means that the pendulum swings faster, resulting in a shorter time for each swing. Since the pendulum is used to measure time in a clock, a shorter time period will cause the clock to lose time.
Calculation:
The change in the length of the seconds pendulum is 0.1 percent, which can be written as 0.001 in decimal form.
The new length of the pendulum is L - 0.001L = 0.999L.
Substituting this value in the formula, we get:
T' = 2π√(0.999L/g)
Now, we can calculate the change in the time period:
ΔT = T - T' = T - 2π√(0.999L/g)
Since the original time period T is 1 second, we have:
ΔT = 1 - 2π√(0.999L/g)
To find the change in time per day, we multiply ΔT by the number of swings per day. In one day, there are 24 hours, 60 minutes per hour, and 60 seconds per minute, giving a total of 24 × 60 × 60 = 86400 seconds.
ΔT per day = ΔT × 86400
Simplifying the equation:
ΔT per day = (1 - 2π√(0.999L/g)) × 86400
Now, let's calculate the approximate value of ΔT per day:
Using the approximation π ≈ 3.14 and g ≈ 9.81 m/s², we substitute these values into the equation.
ΔT per day ≈ (1 - 2 × 3.14√(0.999L/9.81)) × 86400
≈ (1 - 6.28√(L/9.81)) × 86400
≈ 86400 - 6.28 × 9.91√L
≈ 86400 - 62.088√L
We can see that the change in time per day is dependent on the square root of the original length of the pendulum. Since the length of the seconds pendulum L is fixed, the change in time per day will also be constant.
Now, we can analyze the answer options:
a) Loses 43.2 seconds per day: This is not the correct answer because the change in time per day is dependent on the square root of the length of the pendulum, not a constant value.
b) Loses 13.5 seconds per day: This is not the correct answer for the same reason as option a.
c) Los
Given:
The length of the seconds pendulum decreases by 0.1 percent.
To find:
The change in the time on the clock.
Formula:
The time period of a pendulum is given by the formula:
T = 2π√(L/g)
where T is the time period, L is the length of the pendulum, and g is the acceleration due to gravity.
Analysis:
When the length of the pendulum decreases, the time period also decreases. This means that the pendulum swings faster, resulting in a shorter time for each swing. Since the pendulum is used to measure time in a clock, a shorter time period will cause the clock to lose time.
Calculation:
The change in the length of the seconds pendulum is 0.1 percent, which can be written as 0.001 in decimal form.
The new length of the pendulum is L - 0.001L = 0.999L.
Substituting this value in the formula, we get:
T' = 2π√(0.999L/g)
Now, we can calculate the change in the time period:
ΔT = T - T' = T - 2π√(0.999L/g)
Since the original time period T is 1 second, we have:
ΔT = 1 - 2π√(0.999L/g)
To find the change in time per day, we multiply ΔT by the number of swings per day. In one day, there are 24 hours, 60 minutes per hour, and 60 seconds per minute, giving a total of 24 × 60 × 60 = 86400 seconds.
ΔT per day = ΔT × 86400
Simplifying the equation:
ΔT per day = (1 - 2π√(0.999L/g)) × 86400
Now, let's calculate the approximate value of ΔT per day:
Using the approximation π ≈ 3.14 and g ≈ 9.81 m/s², we substitute these values into the equation.
ΔT per day ≈ (1 - 2 × 3.14√(0.999L/9.81)) × 86400
≈ (1 - 6.28√(L/9.81)) × 86400
≈ 86400 - 6.28 × 9.91√L
≈ 86400 - 62.088√L
We can see that the change in time per day is dependent on the square root of the original length of the pendulum. Since the length of the seconds pendulum L is fixed, the change in time per day will also be constant.
Now, we can analyze the answer options:
a) Loses 43.2 seconds per day: This is not the correct answer because the change in time per day is dependent on the square root of the length of the pendulum, not a constant value.
b) Loses 13.5 seconds per day: This is not the correct answer for the same reason as option a.
c) Los

|
Explore Courses for Class 11 exam
|

|
Question Description
The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer?.
The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The length of a second’s pendulum decreases by 0.1percent, then the clocka)Loses 43.2 seconds per dayb)Loses 13.5 seconds per dayc)Loses 7 seconds per dayd)Gains 43.2 seconds per dayCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















