Class 9 Exam > Class 9 Questions > Proof inverse square law?
Start Learning for Free
Proof inverse square law?
Most Upvoted Answer
Proof inverse square law?
Universal law of gravitation: The universal law of gravitation states that every object in the universe attracts every other object with a force called the gravitational force. The force acting between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
Derivation: For two objects of masses ml and m2 and the distance between them r, the force (F) of attraction acting between them is given by the universal law of gravitation as:
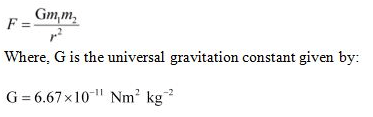
Community Answer
Proof inverse square law?
Proof of the Inverse Square Law
The inverse square law is a fundamental principle in physics that describes the relationship between the intensity of a physical quantity and the distance from its source. It states that the intensity of a physical quantity decreases with the square of the distance from the source.
To understand and prove the inverse square law, we can consider the example of the intensity of light from a point source. Let's break down the proof into the following sections:
1. Definition of Intensity:
- The intensity of a physical quantity is the amount of that quantity per unit area or per unit solid angle.
- In the case of light, it refers to the amount of light energy passing through a unit area per unit time.
2. Intensity at a Distance:
- When a point source emits light, the light spreads out in all directions, forming a sphere with the source at its center.
- As the sphere expands, the same amount of light energy is distributed over a larger surface area.
- Therefore, the intensity of light decreases as the distance from the source increases.
3. Calculation of Intensity:
- The intensity of light at a particular distance can be calculated using the formula:
Intensity = Power/Area
- Assuming the point source emits light uniformly in all directions, the power remains constant regardless of distance.
- The surface area of a sphere is given by the formula:
Area = 4πr^2, where r is the radius or distance from the source.
- Substituting these values into the intensity formula, we get:
Intensity ∝ Power/4πr^2
4. Inverse Square Relationship:
- To prove the inverse square law, we need to show that the intensity is inversely proportional to the square of the distance.
- Let's consider two distances, r1 and r2, where r2 is twice the distance of r1.
- Plugging these distances into the intensity formula, we get:
Intensity1 ∝ Power/4πr1^2
Intensity2 ∝ Power/4πr2^2
- Dividing the two equations, we find:
Intensity2/Intensity1 = (Power/4πr2^2)/(Power/4πr1^2)
Intensity2/Intensity1 = r1^2/r2^2
- Simplifying further, we obtain:
Intensity2/Intensity1 = (r1/r2)^2
- This equation shows that the ratio of intensities is equal to the square of the ratio of distances, proving the inverse square law.
In conclusion, the inverse square law is a fundamental principle that describes the relationship between the intensity of a physical quantity and the distance from its source. The proof demonstrates that the intensity decreases with the square of the distance, as the same amount of energy is spread over a larger surface area. This concept is applicable to various physical phenomena, including light, sound, gravity, and electromagnetic radiation.
The inverse square law is a fundamental principle in physics that describes the relationship between the intensity of a physical quantity and the distance from its source. It states that the intensity of a physical quantity decreases with the square of the distance from the source.
To understand and prove the inverse square law, we can consider the example of the intensity of light from a point source. Let's break down the proof into the following sections:
1. Definition of Intensity:
- The intensity of a physical quantity is the amount of that quantity per unit area or per unit solid angle.
- In the case of light, it refers to the amount of light energy passing through a unit area per unit time.
2. Intensity at a Distance:
- When a point source emits light, the light spreads out in all directions, forming a sphere with the source at its center.
- As the sphere expands, the same amount of light energy is distributed over a larger surface area.
- Therefore, the intensity of light decreases as the distance from the source increases.
3. Calculation of Intensity:
- The intensity of light at a particular distance can be calculated using the formula:
Intensity = Power/Area
- Assuming the point source emits light uniformly in all directions, the power remains constant regardless of distance.
- The surface area of a sphere is given by the formula:
Area = 4πr^2, where r is the radius or distance from the source.
- Substituting these values into the intensity formula, we get:
Intensity ∝ Power/4πr^2
4. Inverse Square Relationship:
- To prove the inverse square law, we need to show that the intensity is inversely proportional to the square of the distance.
- Let's consider two distances, r1 and r2, where r2 is twice the distance of r1.
- Plugging these distances into the intensity formula, we get:
Intensity1 ∝ Power/4πr1^2
Intensity2 ∝ Power/4πr2^2
- Dividing the two equations, we find:
Intensity2/Intensity1 = (Power/4πr2^2)/(Power/4πr1^2)
Intensity2/Intensity1 = r1^2/r2^2
- Simplifying further, we obtain:
Intensity2/Intensity1 = (r1/r2)^2
- This equation shows that the ratio of intensities is equal to the square of the ratio of distances, proving the inverse square law.
In conclusion, the inverse square law is a fundamental principle that describes the relationship between the intensity of a physical quantity and the distance from its source. The proof demonstrates that the intensity decreases with the square of the distance, as the same amount of energy is spread over a larger surface area. This concept is applicable to various physical phenomena, including light, sound, gravity, and electromagnetic radiation.

|
Explore Courses for Class 9 exam
|

|
Question Description
Proof inverse square law? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Proof inverse square law? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Proof inverse square law?.
Proof inverse square law? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Proof inverse square law? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Proof inverse square law?.
Solutions for Proof inverse square law? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of Proof inverse square law? defined & explained in the simplest way possible. Besides giving the explanation of
Proof inverse square law?, a detailed solution for Proof inverse square law? has been provided alongside types of Proof inverse square law? theory, EduRev gives you an
ample number of questions to practice Proof inverse square law? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























