Class 9 Exam > Class 9 Questions > Abcd is a rhombus, eabf is a straight line su...
Start Learning for Free
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.?
Most Upvoted Answer
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove t...
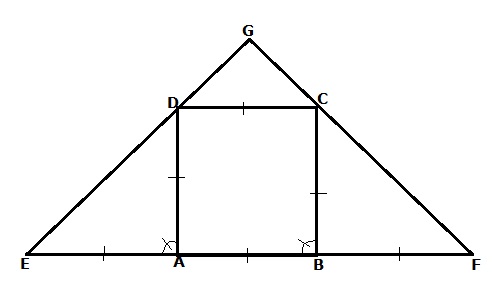

Community Answer
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove t...


|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.?
Question Description
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.?.
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.?.
Solutions for Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? defined & explained in the simplest way possible. Besides giving the explanation of
Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.?, a detailed solution for Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? has been provided alongside types of Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? theory, EduRev gives you an
ample number of questions to practice Abcd is a rhombus, eabf is a straight line such that ea=ab=bf. Prove that ed and fc when produced meet at right angle.? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























