Class 12 Exam > Class 12 Questions > The electron in a hydrogen atom makes transit...
Start Learning for Free
The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron is
- a)9 : 4
- b)81 : 16
- c)4 : 9
- d)16 : 81
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The electron in a hydrogen atom makes transition from M shell to L. Th...
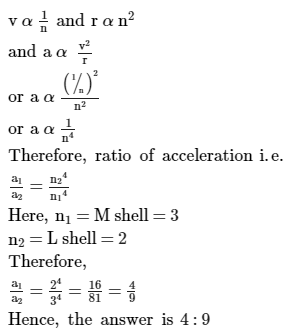
Most Upvoted Answer
The electron in a hydrogen atom makes transition from M shell to L. Th...
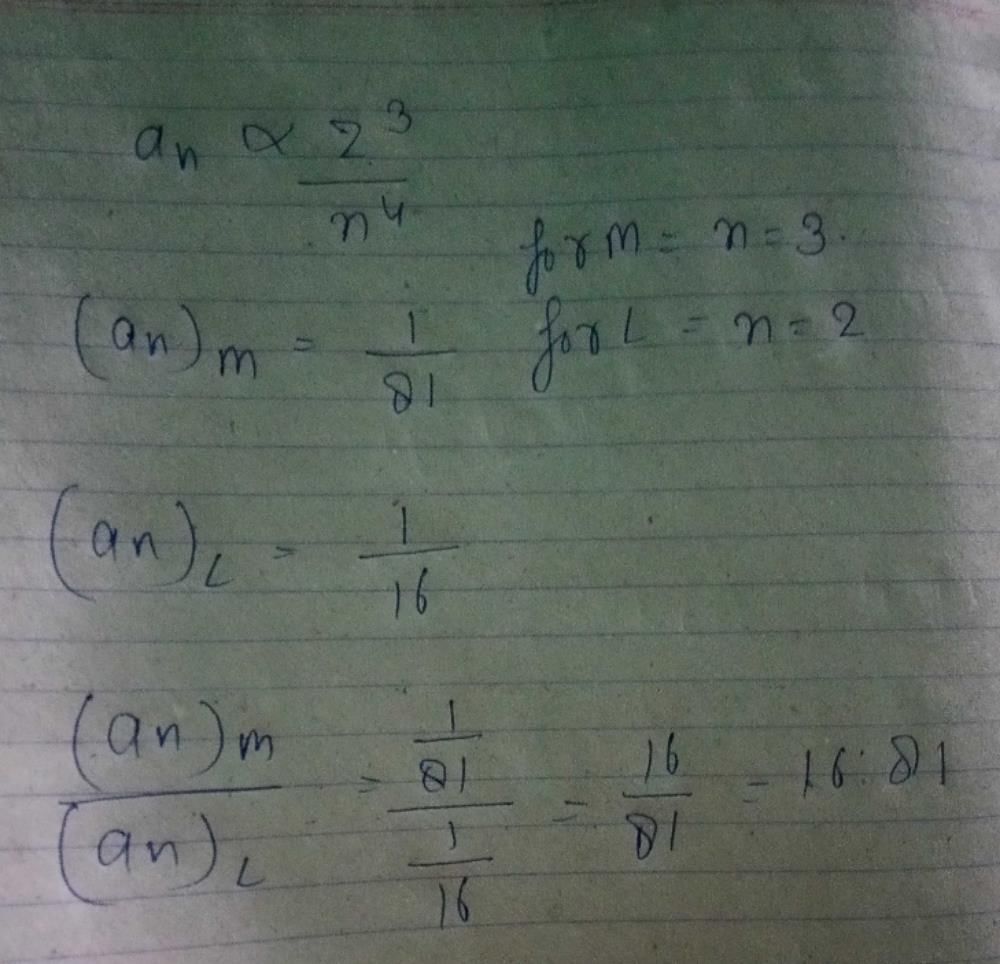
Free Test
FREE
| Start Free Test |
Community Answer
The electron in a hydrogen atom makes transition from M shell to L. Th...
Initial and final states of the electron in a hydrogen atom:
-----------------------------------------------------------
The initial state of the electron in a hydrogen atom is in the M shell, while the final state is in the L shell.
Centripetal acceleration of the electron:
------------------------------------------------
The centripetal acceleration of an object moving in a circular path is given by:
a = v^2 / r
where "a" is the centripetal acceleration, "v" is the velocity of the object, and "r" is the radius of the circular path.
Since the electron is moving in a circular orbit around the nucleus, there must be a centripetal force acting on it, which is provided by the electrostatic attraction between the negatively charged electron and the positively charged nucleus.
The magnitude of the centripetal force is given by:
F = (k * q1 * q2) / r^2
where "F" is the force, "k" is the electrostatic constant, "q1" and "q2" are the charges of the interacting particles (in this case, the charge of the electron and the charge of the nucleus), and "r" is the distance between the particles.
Since the force is equal to the mass of the electron times its centripetal acceleration, we can rewrite the equation as:
(m * a) = (k * q1 * q2) / r^2
where "m" is the mass of the electron.
Using the equation for centripetal acceleration, we can rearrange the equation as:
a = (k * q1 * q2) / (m * r^2)
Ratio of initial to final centripetal acceleration:
---------------------------------------------------------
To find the ratio of the magnitudes of the initial to final centripetal acceleration of the electron, we need to compare the values of "a" for the initial and final states.
Let's denote the initial state as "a_i" and the final state as "a_f".
Using the equation for centripetal acceleration, we can write:
a_i = (k * q1 * q2) / (m * r_i^2)
a_f = (k * q1 * q2) / (m * r_f^2)
where "r_i" and "r_f" are the radii of the M and L shells, respectively.
Dividing the equation for the initial state by the equation for the final state, we get:
(a_i / a_f) = [(k * q1 * q2) / (m * r_i^2)] / [(k * q1 * q2) / (m * r_f^2)]
Simplifying the expression, we find:
(a_i / a_f) = (r_f^2 / r_i^2)
Since the electron is transitioning from the M shell to the L shell, the radius of the L shell is greater than the radius of the M shell.
Therefore, we can conclude that (r_f^2 / r_i^2) > 1.
Hence, the ratio of the magnitudes of the initial to final centripetal acceleration of the electron is greater than 1.
Among the given options, the only one that satisfies this condition is option D, which states that the ratio is 16:81.
-----------------------------------------------------------
The initial state of the electron in a hydrogen atom is in the M shell, while the final state is in the L shell.
Centripetal acceleration of the electron:
------------------------------------------------
The centripetal acceleration of an object moving in a circular path is given by:
a = v^2 / r
where "a" is the centripetal acceleration, "v" is the velocity of the object, and "r" is the radius of the circular path.
Since the electron is moving in a circular orbit around the nucleus, there must be a centripetal force acting on it, which is provided by the electrostatic attraction between the negatively charged electron and the positively charged nucleus.
The magnitude of the centripetal force is given by:
F = (k * q1 * q2) / r^2
where "F" is the force, "k" is the electrostatic constant, "q1" and "q2" are the charges of the interacting particles (in this case, the charge of the electron and the charge of the nucleus), and "r" is the distance between the particles.
Since the force is equal to the mass of the electron times its centripetal acceleration, we can rewrite the equation as:
(m * a) = (k * q1 * q2) / r^2
where "m" is the mass of the electron.
Using the equation for centripetal acceleration, we can rearrange the equation as:
a = (k * q1 * q2) / (m * r^2)
Ratio of initial to final centripetal acceleration:
---------------------------------------------------------
To find the ratio of the magnitudes of the initial to final centripetal acceleration of the electron, we need to compare the values of "a" for the initial and final states.
Let's denote the initial state as "a_i" and the final state as "a_f".
Using the equation for centripetal acceleration, we can write:
a_i = (k * q1 * q2) / (m * r_i^2)
a_f = (k * q1 * q2) / (m * r_f^2)
where "r_i" and "r_f" are the radii of the M and L shells, respectively.
Dividing the equation for the initial state by the equation for the final state, we get:
(a_i / a_f) = [(k * q1 * q2) / (m * r_i^2)] / [(k * q1 * q2) / (m * r_f^2)]
Simplifying the expression, we find:
(a_i / a_f) = (r_f^2 / r_i^2)
Since the electron is transitioning from the M shell to the L shell, the radius of the L shell is greater than the radius of the M shell.
Therefore, we can conclude that (r_f^2 / r_i^2) > 1.
Hence, the ratio of the magnitudes of the initial to final centripetal acceleration of the electron is greater than 1.
Among the given options, the only one that satisfies this condition is option D, which states that the ratio is 16:81.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer?
Question Description
The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer?.
The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer?.
Solutions for The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer?, a detailed solution for The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The electron in a hydrogen atom makes transition from M shell to L. The ratio of magnitudes of initial to final centripetal acceleration of the electron isa)9 : 4b)81 : 16c)4 : 9d)16 : 81Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















