Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > In the quadrantal bearing system, a whole cir...
Start Learning for Free
In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:
- a)N 660 30' W
- b)S 1130 30' N
- c)N 230 30' W
- d)W 230 30' N
Correct answer is option 'B. Can you explain this answer?
Most Upvoted Answer
In the quadrantal bearing system, a whole circle bearing of 2930 30' c...
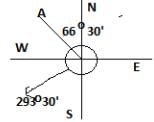
Whole circle bearing = 293 degree 30'
Q.C.B = 360 degree - 293 degree 30' = 66 degree 30'
Q.C.B = N 66 degree 30' W
Community Answer
In the quadrantal bearing system, a whole circle bearing of 2930 30' c...
Quadrantal Bearing System:
The quadrantal bearing system is one of the three types of bearing systems used in land navigation. It is based on the idea of dividing the circle into four quadrants, and expressing bearings in terms of the compass direction in which they lie.
Each quadrant is named for the cardinal direction that it contains, with the first letter capitalized. For example, the northeast quadrant is called the NE quadrant.
The bearings in this system are expressed as the angle between the reference direction (north or south) and the line of sight to the point of interest. The reference direction is indicated by the first letter of the bearing, which is either N or S.
Solution:
The given whole circle bearing of 2930 30' can be expressed as a quadrantal bearing as follows:
- The bearing lies in the northwest quadrant, which is indicated by the letter N.
- The angle between the reference direction (north) and the line of sight to the point of interest is 2930 30'.
- Therefore, the quadrantal bearing is N 2930 30' W.
However, this is not one of the options given in the question. To express this bearing as one of the given options, we need to subtract it from 3600 and express the result in the opposite quadrant.
- 3600 - 2930 30' = 6630 30'
- The opposite quadrant to the northwest quadrant is the southeast quadrant, which is indicated by the letter S.
- Therefore, the quadrantal bearing can be expressed as S 6630 30' N.
This is equivalent to option B: S 1130 30' N.
Therefore, the correct answer is option B: S 1130 30' N.
The quadrantal bearing system is one of the three types of bearing systems used in land navigation. It is based on the idea of dividing the circle into four quadrants, and expressing bearings in terms of the compass direction in which they lie.
Each quadrant is named for the cardinal direction that it contains, with the first letter capitalized. For example, the northeast quadrant is called the NE quadrant.
The bearings in this system are expressed as the angle between the reference direction (north or south) and the line of sight to the point of interest. The reference direction is indicated by the first letter of the bearing, which is either N or S.
Solution:
The given whole circle bearing of 2930 30' can be expressed as a quadrantal bearing as follows:
- The bearing lies in the northwest quadrant, which is indicated by the letter N.
- The angle between the reference direction (north) and the line of sight to the point of interest is 2930 30'.
- Therefore, the quadrantal bearing is N 2930 30' W.
However, this is not one of the options given in the question. To express this bearing as one of the given options, we need to subtract it from 3600 and express the result in the opposite quadrant.
- 3600 - 2930 30' = 6630 30'
- The opposite quadrant to the northwest quadrant is the southeast quadrant, which is indicated by the letter S.
- Therefore, the quadrantal bearing can be expressed as S 6630 30' N.
This is equivalent to option B: S 1130 30' N.
Therefore, the correct answer is option B: S 1130 30' N.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer?.
In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer?.
Solutions for In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer?, a detailed solution for In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? has been provided alongside types of In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In the quadrantal bearing system, a whole circle bearing of 2930 30' can be expressed as:a)N 660 30' Wb)S 1130 30' Nc)N 230 30' Wd)W 230 30' NCorrect answer is option 'B. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















