Class 11 Exam > Class 11 Questions > A simple pendulum with length l and bob of ma...
Start Learning for Free
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will be
- a)mg
- b)
- c)
- d)mg[1 + (a/l) ]
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
A simple pendulum with length l and bob of mass m is executing S.H.M o...
The tension in the string would be maximum when bob will be passing mean position.
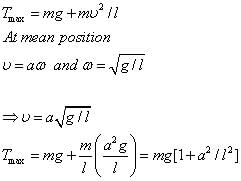
View all questions of this test
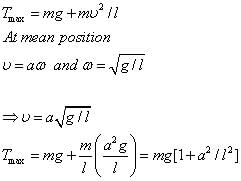
Most Upvoted Answer
A simple pendulum with length l and bob of mass m is executing S.H.M o...
The maximum tension in the string of a simple pendulum executing simple harmonic motion can be determined by considering the forces acting on the bob at the extreme points of its motion.
1. Forces acting on the bob:
At the extreme points of its motion, the bob experiences two forces:
- The weight force (mg) acting vertically downward.
- The tension force (T) acting along the length of the string.
2. Maximum tension:
To find the maximum tension, we need to consider the point where the tension is maximum, which is at the extreme points of the motion, when the bob is farthest from the equilibrium position.
3. Analyzing the forces:
At the extreme points of the motion, the bob is at its maximum displacement (a) from the equilibrium position. Therefore, the tension force (T) is at its maximum value.
4. Resolving the forces:
We can resolve the weight force (mg) into two components:
- The component parallel to the direction of displacement (a) is mg * (a/l).
- The component perpendicular to the direction of displacement is mg * (1 - a^2/l^2)^0.5.
5. Equilibrium condition:
At the extreme points of the motion, the bob is momentarily at rest. This means that the net force acting on the bob is zero.
6. Calculating the tension:
To find the maximum tension, we equate the sum of the components of the weight force and the tension force to zero.
7. Applying the equilibrium condition:
The net force in the vertical direction is zero, so we equate the sum of the components of the weight force and the tension force in the vertical direction to zero.
8. Mathematical calculation:
mg * (1 - a^2/l^2)^0.5 + T - mg = 0
9. Simplification:
T = mg - mg * (1 - a^2/l^2)^0.5
10. Further simplification:
T = mg * [1 - (1 - a^2/l^2)^0.5]
11. Final expression:
T = mg * [1 - (1 - a^2/l^2)]
T = mg * [1 - 1 + a^2/l^2]
T = mg * (a^2/l^2)
Therefore, the expression for the maximum tension in the string is mg * (a^2/l^2), which corresponds to option B.
1. Forces acting on the bob:
At the extreme points of its motion, the bob experiences two forces:
- The weight force (mg) acting vertically downward.
- The tension force (T) acting along the length of the string.
2. Maximum tension:
To find the maximum tension, we need to consider the point where the tension is maximum, which is at the extreme points of the motion, when the bob is farthest from the equilibrium position.
3. Analyzing the forces:
At the extreme points of the motion, the bob is at its maximum displacement (a) from the equilibrium position. Therefore, the tension force (T) is at its maximum value.
4. Resolving the forces:
We can resolve the weight force (mg) into two components:
- The component parallel to the direction of displacement (a) is mg * (a/l).
- The component perpendicular to the direction of displacement is mg * (1 - a^2/l^2)^0.5.
5. Equilibrium condition:
At the extreme points of the motion, the bob is momentarily at rest. This means that the net force acting on the bob is zero.
6. Calculating the tension:
To find the maximum tension, we equate the sum of the components of the weight force and the tension force to zero.
7. Applying the equilibrium condition:
The net force in the vertical direction is zero, so we equate the sum of the components of the weight force and the tension force in the vertical direction to zero.
8. Mathematical calculation:
mg * (1 - a^2/l^2)^0.5 + T - mg = 0
9. Simplification:
T = mg - mg * (1 - a^2/l^2)^0.5
10. Further simplification:
T = mg * [1 - (1 - a^2/l^2)^0.5]
11. Final expression:
T = mg * [1 - (1 - a^2/l^2)]
T = mg * [1 - 1 + a^2/l^2]
T = mg * (a^2/l^2)
Therefore, the expression for the maximum tension in the string is mg * (a^2/l^2), which corresponds to option B.
Free Test
FREE
| Start Free Test |
Community Answer
A simple pendulum with length l and bob of mass m is executing S.H.M o...
The tension in the string would be maximum when bob will be passing mean position.



|
Explore Courses for Class 11 exam
|

|
Question Description
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer?.
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer?.
Solutions for A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will bea)mgb)c)d)mg[1 + (a/l) ]Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















