Physics Exam > Physics Questions > Thermal neutrons (energy = 300 kB = 0.025 eV)...
Start Learning for Free
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used is
- a)0.01 nm
- b)0.05 nm
- c)0.1 nm
- d)0.15 nm
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for s...
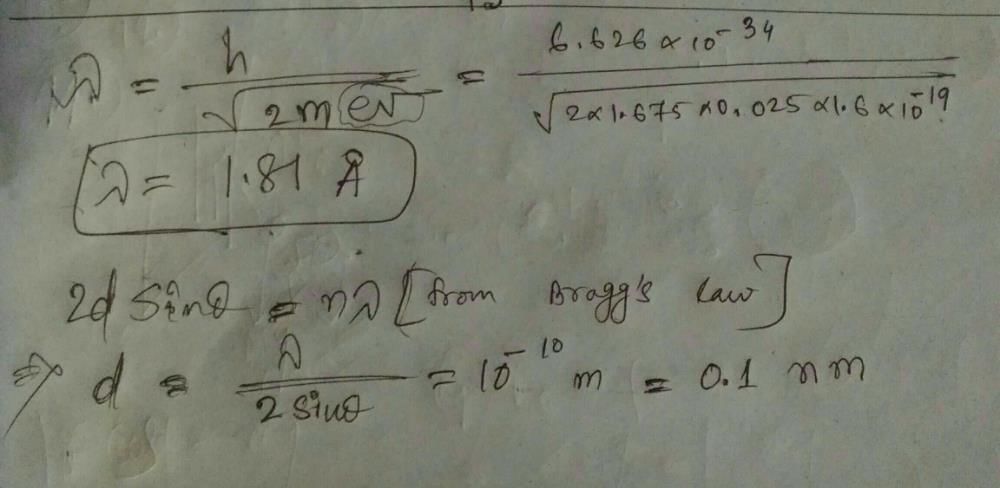
Free Test
FREE
| Start Free Test |
Community Answer
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for s...
Introduction:
Thermal neutrons are neutrons with low energy, typically around 0.025 electron volts (eV). They are often used in materials science for structural determination, particularly in techniques such as neutron diffraction. The lattice spacing of a material refers to the distance between the repeating units or lattice points in its crystal structure. In this question, we are asked to determine the typical lattice spacing of a material that can be studied using thermal neutrons.
Explanation:
To understand why the correct answer is option 'A' (0.01 nm), let's consider the principles behind neutron diffraction and how it relates to the lattice spacing of a material.
Neutron Diffraction:
Neutron diffraction is a technique used to study the crystal structure of materials. When a beam of neutrons interacts with a crystal, it undergoes scattering due to the interaction with the atomic nuclei in the crystal lattice. This scattering pattern can be analyzed to determine the arrangement of atoms within the crystal.
De Broglie Wavelength:
The scattering of neutrons in a crystal is governed by their de Broglie wavelength, which is given by the equation λ = h/p, where λ is the wavelength, h is the Planck constant, and p is the momentum of the neutron. Since the energy of thermal neutrons is known (0.025 eV), we can use the relation E = p^2/2m, where E is the energy, p is the momentum, and m is the mass of the neutron, to determine the momentum of the neutron.
Determination of Neutron Momentum:
1. Given energy of the thermal neutron: E = 0.025 eV
2. Mass of neutron: m = 1.675 x 10^-27 kg (approximate value)
3. Rearranging the energy equation, we can solve for momentum (p): p^2 = 2mE
4. Plugging in the values, we have: p^2 = 2 * (1.675 x 10^-27 kg) * (0.025 eV)
5. Converting electron volts (eV) to joules (J): 1 eV = 1.602 x 10^-19 J
6. Substituting the values and simplifying, we find: p^2 ≈ 2 * (1.675 x 10^-27 kg) * (0.025 eV) * (1.602 x 10^-19 J/eV)
p^2 ≈ 6.708 x 10^-47 kg·m^2/s^2
Wavelength Calculation:
7. Using the de Broglie wavelength equation, λ = h/p, and substituting the known values, we can calculate the wavelength of the neutron: λ ≈ (6.626 x 10^-34 J·s) / √(6.708 x 10^-47 kg·m^2/s^2)
λ ≈ 1.17 x 10^-10 m
Relationship between Lattice Spacing and Wavelength:
8. In a crystal lattice, the spacing between neighboring lattice points is related to the wavelength of the probing radiation. For constructive interference to occur, the scattering angle must satisfy the Bragg condition:
Thermal neutrons are neutrons with low energy, typically around 0.025 electron volts (eV). They are often used in materials science for structural determination, particularly in techniques such as neutron diffraction. The lattice spacing of a material refers to the distance between the repeating units or lattice points in its crystal structure. In this question, we are asked to determine the typical lattice spacing of a material that can be studied using thermal neutrons.
Explanation:
To understand why the correct answer is option 'A' (0.01 nm), let's consider the principles behind neutron diffraction and how it relates to the lattice spacing of a material.
Neutron Diffraction:
Neutron diffraction is a technique used to study the crystal structure of materials. When a beam of neutrons interacts with a crystal, it undergoes scattering due to the interaction with the atomic nuclei in the crystal lattice. This scattering pattern can be analyzed to determine the arrangement of atoms within the crystal.
De Broglie Wavelength:
The scattering of neutrons in a crystal is governed by their de Broglie wavelength, which is given by the equation λ = h/p, where λ is the wavelength, h is the Planck constant, and p is the momentum of the neutron. Since the energy of thermal neutrons is known (0.025 eV), we can use the relation E = p^2/2m, where E is the energy, p is the momentum, and m is the mass of the neutron, to determine the momentum of the neutron.
Determination of Neutron Momentum:
1. Given energy of the thermal neutron: E = 0.025 eV
2. Mass of neutron: m = 1.675 x 10^-27 kg (approximate value)
3. Rearranging the energy equation, we can solve for momentum (p): p^2 = 2mE
4. Plugging in the values, we have: p^2 = 2 * (1.675 x 10^-27 kg) * (0.025 eV)
5. Converting electron volts (eV) to joules (J): 1 eV = 1.602 x 10^-19 J
6. Substituting the values and simplifying, we find: p^2 ≈ 2 * (1.675 x 10^-27 kg) * (0.025 eV) * (1.602 x 10^-19 J/eV)
p^2 ≈ 6.708 x 10^-47 kg·m^2/s^2
Wavelength Calculation:
7. Using the de Broglie wavelength equation, λ = h/p, and substituting the known values, we can calculate the wavelength of the neutron: λ ≈ (6.626 x 10^-34 J·s) / √(6.708 x 10^-47 kg·m^2/s^2)
λ ≈ 1.17 x 10^-10 m
Relationship between Lattice Spacing and Wavelength:
8. In a crystal lattice, the spacing between neighboring lattice points is related to the wavelength of the probing radiation. For constructive interference to occur, the scattering angle must satisfy the Bragg condition:
|
Explore Courses for Physics exam
|
|
Similar Physics Doubts
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer?
Question Description
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer?.
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Thermal neutrons (energy = 300 kB = 0.025 eV) are sometimes used for structural determination of materials. The typical lattice spacing of a material for which these can be used isa)0.01 nmb)0.05 nmc)0.1 nmd)0.15 nmCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Physics tests.
|
|
Explore Courses for Physics exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup