Chemistry Exam > Chemistry Questions > The electrochemical cell shown below is a con...
Start Learning for Free
The electrochemical cell shown below is a concentration cell.
M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.
The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.
M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.
The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.
Q.
The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)
- a)1 × 10–15
- b)4 × 10–15
- c)1 × 10–12
- d)4 × 10–12
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
The electrochemical cell shown below is a concentration cell.M|M2+ (sa...
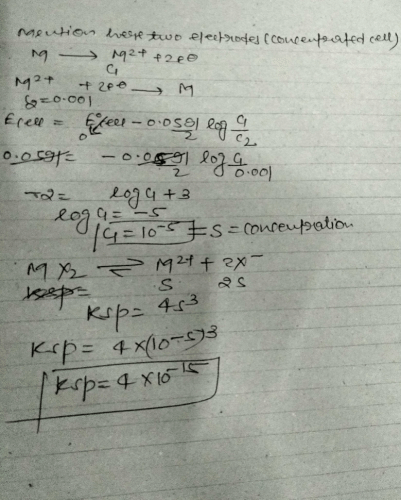
Community Answer
The electrochemical cell shown below is a concentration cell.M|M2+ (sa...
Given information:
- Electrochemical cell is a concentration cell.
- Half-cell reactions: M+ + e- → M (saturated solution of a sparingly soluble salt, MX2)
M2+ + 2e- → M (0.001 mol dm-3)
- EMF of the cell at 298K = 0.059 V
- 2.303RT/F = 0.059 V (at 298K)
To find: Solubility product (Ksp) of MX2 at 298K
Solution:
The given cell is a concentration cell, which means that the two half-cells have the same electrode but different concentrations of M2+ ions. The concentration of M2+ ions at the two electrodes can be related to the solubility product of MX2 using the Nernst equation:
Ecell = E°cell - (RT/nF) ln Q
where Ecell is the cell potential, E°cell is the standard cell potential, R is the gas constant, T is the temperature, n is the number of electrons transferred in the cell reaction, F is the Faraday constant, and Q is the reaction quotient.
For the given cell, the half-cell reactions and their standard reduction potentials are:
M+ + e- → M (saturated solution of a sparingly soluble salt, MX2) E°1 = ?
M2+ + 2e- → M E°2 = E°°M2+/M - E°°M
The standard potential of the M2+/M half-reaction can be calculated using the Nernst equation:
E°°M2+/M = (RT/nF) ln(Ksp)
where Ksp is the solubility product of MX2.
Substituting the given values into the Nernst equation for the cell:
0.059 V = E°1 - (RT/nF) ln(Q)
where Q = [M2+] / [M+] (the concentration of M+ ions is assumed to be constant and equal to the saturation concentration)
Taking the antilog of both sides:
Q = [M2+] / [M+] = e^(nF(E°1 - 0.059 V) / RT)
Substituting the standard potential of the M2+/M half-reaction and rearranging:
Ksp = [M2+]^2 [M+]^-1 = e^(2nF(E°1 - 0.059 V) / RT)
Using the value of 2.303RT/F = 0.059 V at 298K and n = 2 (since two electrons are transferred in the cell reaction):
Ksp = e^(4.605(E°1 - 0.059) / 0.059) = e^(78.0508E°1 - 78.0508)
Taking the antilog of both sides:
Ksp = 10^(78.0508E°1 - 78.0508)
To find the value of E°1, we can use the standard potentials of the half-reactions for M and M2+ ions:
E°1 = E°°M - E°°M2+/M = E°°M - (RT/2F) ln([M2+]/[M])
Substituting the given values:
E°1 = -0.059 - (
- Electrochemical cell is a concentration cell.
- Half-cell reactions: M+ + e- → M (saturated solution of a sparingly soluble salt, MX2)
M2+ + 2e- → M (0.001 mol dm-3)
- EMF of the cell at 298K = 0.059 V
- 2.303RT/F = 0.059 V (at 298K)
To find: Solubility product (Ksp) of MX2 at 298K
Solution:
The given cell is a concentration cell, which means that the two half-cells have the same electrode but different concentrations of M2+ ions. The concentration of M2+ ions at the two electrodes can be related to the solubility product of MX2 using the Nernst equation:
Ecell = E°cell - (RT/nF) ln Q
where Ecell is the cell potential, E°cell is the standard cell potential, R is the gas constant, T is the temperature, n is the number of electrons transferred in the cell reaction, F is the Faraday constant, and Q is the reaction quotient.
For the given cell, the half-cell reactions and their standard reduction potentials are:
M+ + e- → M (saturated solution of a sparingly soluble salt, MX2) E°1 = ?
M2+ + 2e- → M E°2 = E°°M2+/M - E°°M
The standard potential of the M2+/M half-reaction can be calculated using the Nernst equation:
E°°M2+/M = (RT/nF) ln(Ksp)
where Ksp is the solubility product of MX2.
Substituting the given values into the Nernst equation for the cell:
0.059 V = E°1 - (RT/nF) ln(Q)
where Q = [M2+] / [M+] (the concentration of M+ ions is assumed to be constant and equal to the saturation concentration)
Taking the antilog of both sides:
Q = [M2+] / [M+] = e^(nF(E°1 - 0.059 V) / RT)
Substituting the standard potential of the M2+/M half-reaction and rearranging:
Ksp = [M2+]^2 [M+]^-1 = e^(2nF(E°1 - 0.059 V) / RT)
Using the value of 2.303RT/F = 0.059 V at 298K and n = 2 (since two electrons are transferred in the cell reaction):
Ksp = e^(4.605(E°1 - 0.059) / 0.059) = e^(78.0508E°1 - 78.0508)
Taking the antilog of both sides:
Ksp = 10^(78.0508E°1 - 78.0508)
To find the value of E°1, we can use the standard potentials of the half-reactions for M and M2+ ions:
E°1 = E°°M - E°°M2+/M = E°°M - (RT/2F) ln([M2+]/[M])
Substituting the given values:
E°1 = -0.059 - (

|
Explore Courses for Chemistry exam
|

|
The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer?
Question Description
The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer?.
The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer?.
Solutions for The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemistry.
Download more important topics, notes, lectures and mock test series for Chemistry Exam by signing up for free.
Here you can find the meaning of The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer?, a detailed solution for The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The electrochemical cell shown below is a concentration cell.M|M2+ (saturated solut ion of a sparingly so luble salt, MX2 || M2+ (0.001 mol dm–3)| M.The emf of the cell depends on the difference in concentration of M2+ ions at the two electrodes. The emf of the cell at 298 is 0.059 V.Q.The solubility product (Ksp ; mol3 dm–9) of MX2 at 298 based on the informat ion available the given concentration cell is (take 2.303 × R × 298/F = 0.059 V)a)1 × 10–15b)4 × 10–15c)1 × 10–12d)4 × 10–12Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Chemistry tests.

|
Explore Courses for Chemistry exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

















