Class 11 Exam > Class 11 Questions > Equations of a stationary wave and a travelli...
Start Learning for Free
Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how?
Verified Answer
Equations of a stationary wave and a travelling wave are as follows: y...
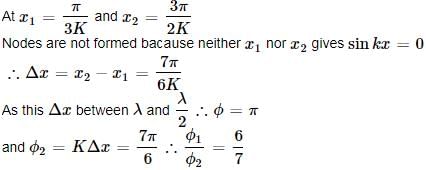
 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
Equations of a stationary wave and a travelling wave are as follows: y...
Stationary Wave:
A stationary wave is a wave that appears to be standing still, as opposed to a traveling wave that moves through space. It is formed by the superposition of two waves of the same frequency and amplitude, traveling in opposite directions. The equation of a stationary wave can be written as y1 = a sinkxcoswt, where a represents the amplitude, k is the wave number, x is the position, and w is the angular frequency.
Travelling Wave:
A traveling wave is a wave that propagates through space, carrying energy from one point to another. It is characterized by its amplitude, wavelength, and frequency. The equation of a traveling wave can be written as y2 = asin(kx - wt), where a represents the amplitude, k is the wave number, x is the position, and w is the angular frequency.
Phase Difference:
The phase difference between two points in a wave is the fraction of a complete cycle that one point is ahead or behind the other point. It is usually measured in radians or degrees. In this case, we need to find the phase difference between two points x1 = pi/3k and x2 = 3pi/2k for the stationary and traveling waves.
Calculating Phase Difference:
To calculate the phase difference, we need to compare the arguments of the trigonometric functions in the equations of the waves.
For the stationary wave:
y1 = a sinkxcoswt
At x1 = pi/3k: Argument = k(pi/3k)coswt = (pi/3)coswt
For the traveling wave:
y2 = asin(kx - wt)
At x2 = 3pi/2k: Argument = k(3pi/2k) - wt = 3pi/2 - wt
Now, we can compare the arguments to find the phase difference between the two points.
Comparing Arguments:
Argument at x1 = pi/3k: (pi/3)coswt
Argument at x2 = 3pi/2k: 3pi/2 - wt
To find the phase difference, we need to equate the two arguments and solve for wt.
(pi/3)coswt = 3pi/2 - wt
Simplifying the equation, we get:
(pi/3)coswt + wt = 3pi/2
This equation cannot be solved analytically to find a specific value for wt. However, we can still calculate the ratio A/B using numerical methods or approximations.
Calculating the Ratio A/B:
Let's assume a value for wt, for example, wt = 0. Then we can solve the equation to find the corresponding values of the arguments at x1 and x2.
Argument at x1 = pi/3k: (pi/3)cos(0) = pi/3
Argument at x2 = 3pi/2k: 3pi/2 - (0) = 3pi/2
Now we can calculate the ratio A/B:
A = pi/3
B = 3pi/2
Ratio A/B = (pi/3)/(3pi/2) = 2/9
Using numerical methods or approximations, we can repeat this process for different values
A stationary wave is a wave that appears to be standing still, as opposed to a traveling wave that moves through space. It is formed by the superposition of two waves of the same frequency and amplitude, traveling in opposite directions. The equation of a stationary wave can be written as y1 = a sinkxcoswt, where a represents the amplitude, k is the wave number, x is the position, and w is the angular frequency.
Travelling Wave:
A traveling wave is a wave that propagates through space, carrying energy from one point to another. It is characterized by its amplitude, wavelength, and frequency. The equation of a traveling wave can be written as y2 = asin(kx - wt), where a represents the amplitude, k is the wave number, x is the position, and w is the angular frequency.
Phase Difference:
The phase difference between two points in a wave is the fraction of a complete cycle that one point is ahead or behind the other point. It is usually measured in radians or degrees. In this case, we need to find the phase difference between two points x1 = pi/3k and x2 = 3pi/2k for the stationary and traveling waves.
Calculating Phase Difference:
To calculate the phase difference, we need to compare the arguments of the trigonometric functions in the equations of the waves.
For the stationary wave:
y1 = a sinkxcoswt
At x1 = pi/3k: Argument = k(pi/3k)coswt = (pi/3)coswt
For the traveling wave:
y2 = asin(kx - wt)
At x2 = 3pi/2k: Argument = k(3pi/2k) - wt = 3pi/2 - wt
Now, we can compare the arguments to find the phase difference between the two points.
Comparing Arguments:
Argument at x1 = pi/3k: (pi/3)coswt
Argument at x2 = 3pi/2k: 3pi/2 - wt
To find the phase difference, we need to equate the two arguments and solve for wt.
(pi/3)coswt = 3pi/2 - wt
Simplifying the equation, we get:
(pi/3)coswt + wt = 3pi/2
This equation cannot be solved analytically to find a specific value for wt. However, we can still calculate the ratio A/B using numerical methods or approximations.
Calculating the Ratio A/B:
Let's assume a value for wt, for example, wt = 0. Then we can solve the equation to find the corresponding values of the arguments at x1 and x2.
Argument at x1 = pi/3k: (pi/3)cos(0) = pi/3
Argument at x2 = 3pi/2k: 3pi/2 - (0) = 3pi/2
Now we can calculate the ratio A/B:
A = pi/3
B = 3pi/2
Ratio A/B = (pi/3)/(3pi/2) = 2/9
Using numerical methods or approximations, we can repeat this process for different values
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how?
Question Description
Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how?.
Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how?.
Solutions for Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? defined & explained in the simplest way possible. Besides giving the explanation of
Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how?, a detailed solution for Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? has been provided alongside types of Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? theory, EduRev gives you an
ample number of questions to practice Equations of a stationary wave and a travelling wave are as follows: y1 = a sinkxcoswt and y2 = asin( kx- wt). The phase difference between two points x1 = pi/3k and x2= 3pi/2k are A and B respectively for the two waves. The ratio A/B is 1 5/6 3/4 6/7 Ans is 6/7 . how? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























