JEE Exam > JEE Questions > The sum of the frequencies of the first overt...
Start Learning for Free
The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe?
Most Upvoted Answer
The sum of the frequencies of the first overtone of a closed pipe and ...
**Solution:**
Let's solve the problem step by step.
**Step 1: Understanding the concept of overtones**
In acoustics, an overtone is a higher frequency vibration that is a multiple of the fundamental frequency. Overtones are also known as harmonics. The first overtone has a frequency twice that of the fundamental frequency, the second overtone has a frequency three times that of the fundamental frequency, and so on.
**Step 2: Analyzing the given information**
According to the problem, we are given the sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length, which is 180. Let's assume the fundamental frequency of the closed pipe is f and the fundamental frequency of the open pipe is g.
We know that the frequency of the first overtone of a closed pipe is 2f, and the frequency of the second overtone of an open pipe is 3g.
So, based on the given information, we can form the equation:
2f + 3g = 180
**Step 3: Finding the fundamental frequencies**
To find the fundamental frequencies of the closed and open pipes, we need to solve the equation formed in the previous step. However, we need another equation to solve the system of equations.
**Step 4: Analyzing the length of the pipes**
Since the first overtone of a closed pipe and the second overtone of an open pipe have the same length, we can use the formula for the fundamental frequency of a closed pipe and an open pipe to form another equation.
The formula for the fundamental frequency of a closed pipe is:
f = v / (2L)
Where f is the frequency, v is the speed of sound in air, and L is the length of the pipe.
The formula for the fundamental frequency of an open pipe is:
g = v / (2L)
Where g is the frequency, v is the speed of sound in air, and L is the length of the pipe.
Since the length of the pipes is the same, we can equate the two equations:
v / (2L) = v / (2L)
**Step 5: Solving the system of equations**
Now we have two equations:
2f + 3g = 180
v / (2L) = v / (2L)
Simplifying the second equation, we get:
1 = 1
This equation does not provide any useful information, so we can disregard it.
Now we can solve the system of equations:
2f + 3g = 180
We have two variables and one equation, which means we can't find the exact values of f and g. However, we can find their ratio.
Divide both sides of the equation by 2:
f + (3/2)g = 90
Now we can express f in terms of g:
f = 90 - (3/2)g
**Step 6: Conclusion**
In conclusion, we have found the relationship between the fundamental frequencies of the closed and open pipes. The fundamental frequency of the closed pipe (f) is equal to 90 minus one and a half times the fundamental frequency of the open pipe (g).
Unfortunately, without additional information or constraints, we cannot determine the exact values of f and g. The problem does not provide any information about the speed of
Let's solve the problem step by step.
**Step 1: Understanding the concept of overtones**
In acoustics, an overtone is a higher frequency vibration that is a multiple of the fundamental frequency. Overtones are also known as harmonics. The first overtone has a frequency twice that of the fundamental frequency, the second overtone has a frequency three times that of the fundamental frequency, and so on.
**Step 2: Analyzing the given information**
According to the problem, we are given the sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length, which is 180. Let's assume the fundamental frequency of the closed pipe is f and the fundamental frequency of the open pipe is g.
We know that the frequency of the first overtone of a closed pipe is 2f, and the frequency of the second overtone of an open pipe is 3g.
So, based on the given information, we can form the equation:
2f + 3g = 180
**Step 3: Finding the fundamental frequencies**
To find the fundamental frequencies of the closed and open pipes, we need to solve the equation formed in the previous step. However, we need another equation to solve the system of equations.
**Step 4: Analyzing the length of the pipes**
Since the first overtone of a closed pipe and the second overtone of an open pipe have the same length, we can use the formula for the fundamental frequency of a closed pipe and an open pipe to form another equation.
The formula for the fundamental frequency of a closed pipe is:
f = v / (2L)
Where f is the frequency, v is the speed of sound in air, and L is the length of the pipe.
The formula for the fundamental frequency of an open pipe is:
g = v / (2L)
Where g is the frequency, v is the speed of sound in air, and L is the length of the pipe.
Since the length of the pipes is the same, we can equate the two equations:
v / (2L) = v / (2L)
**Step 5: Solving the system of equations**
Now we have two equations:
2f + 3g = 180
v / (2L) = v / (2L)
Simplifying the second equation, we get:
1 = 1
This equation does not provide any useful information, so we can disregard it.
Now we can solve the system of equations:
2f + 3g = 180
We have two variables and one equation, which means we can't find the exact values of f and g. However, we can find their ratio.
Divide both sides of the equation by 2:
f + (3/2)g = 90
Now we can express f in terms of g:
f = 90 - (3/2)g
**Step 6: Conclusion**
In conclusion, we have found the relationship between the fundamental frequencies of the closed and open pipes. The fundamental frequency of the closed pipe (f) is equal to 90 minus one and a half times the fundamental frequency of the open pipe (g).
Unfortunately, without additional information or constraints, we cannot determine the exact values of f and g. The problem does not provide any information about the speed of
Community Answer
The sum of the frequencies of the first overtone of a closed pipe and ...
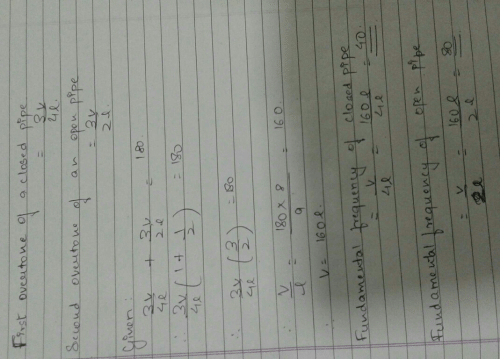

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe?
Question Description
The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe?.
The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe?.
Solutions for The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? defined & explained in the simplest way possible. Besides giving the explanation of
The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe?, a detailed solution for The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? has been provided alongside types of The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? theory, EduRev gives you an
ample number of questions to practice The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 what are the fundamental frequencies of closed and open pipe? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























