Class 9 Exam > Class 9 Questions > Prove that the Rhombus inscribed in a circle ...
Start Learning for Free
Prove that the Rhombus inscribed in a circle is a square?
Most Upvoted Answer
Prove that the Rhombus inscribed in a circle is a square?
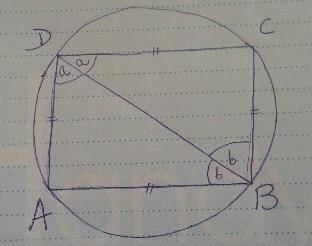
To prove rhombus inscribed in a circle is a square,we need to prove that either any one of its interior angles is equal to 90degree or its diagonals are equal.
In the figure,diagonal BD is angular bisector of angle B and angle D.
In triangle ABD and BCD,
AD=BC (sides of rhombus are equal)
AB=CD (sides of rhombus are equal)
BD=BD (common side)
△ABD ≅ △BCD. (SSS congruency)
In the figure,
2a + 2b = 180degree (as, opposite angles of a cyclic quadrilateral are always supplementary)
2(a+b)=180degree
a+b=degree
In △ABD,
Angle A = degree -(a+b)
=degree -90degree
=90degree
Therefore,proved that one of it's interior angle is 90degree
Community Answer
Prove that the Rhombus inscribed in a circle is a square?
Proof that the Rhombus inscribed in a circle is a square:
To prove that a rhombus inscribed in a circle is a square, we need to show that all four sides of the rhombus are congruent and all angles are right angles.
Step 1: Inscribed Angle Property
- Start by considering the properties of an inscribed angle. In a circle, an inscribed angle is equal to half the measure of the intercepted arc.
- Since a rhombus inscribed in a circle has opposite angles that are congruent, each angle of the rhombus is half the measure of the intercepted arc.
- Therefore, all four angles of the rhombus are congruent.
Step 2: Opposite Angles of a Rhombus
- In a rhombus, opposite angles are congruent.
- Since all four angles of the rhombus are congruent, it implies that opposite angles are right angles.
Step 3: Diagonals of a Rhombus
- The diagonals of a rhombus are perpendicular bisectors of each other.
- Since opposite angles of the rhombus are right angles, the diagonals are perpendicular to each other.
Step 4: Congruent Sides
- The diagonals of a rhombus also bisect each other, forming four congruent right triangles.
- Each right triangle has two congruent sides (the diagonals) and the hypotenuse (side of the rhombus).
- By the hypotenuse-leg congruence theorem, the four sides of the rhombus are congruent.
Conclusion:
- We have shown that all four angles of the rhombus are right angles and all four sides are congruent.
- By definition, a quadrilateral with four right angles and congruent sides is a square.
- Therefore, a rhombus inscribed in a circle is a square.
To prove that a rhombus inscribed in a circle is a square, we need to show that all four sides of the rhombus are congruent and all angles are right angles.
Step 1: Inscribed Angle Property
- Start by considering the properties of an inscribed angle. In a circle, an inscribed angle is equal to half the measure of the intercepted arc.
- Since a rhombus inscribed in a circle has opposite angles that are congruent, each angle of the rhombus is half the measure of the intercepted arc.
- Therefore, all four angles of the rhombus are congruent.
Step 2: Opposite Angles of a Rhombus
- In a rhombus, opposite angles are congruent.
- Since all four angles of the rhombus are congruent, it implies that opposite angles are right angles.
Step 3: Diagonals of a Rhombus
- The diagonals of a rhombus are perpendicular bisectors of each other.
- Since opposite angles of the rhombus are right angles, the diagonals are perpendicular to each other.
Step 4: Congruent Sides
- The diagonals of a rhombus also bisect each other, forming four congruent right triangles.
- Each right triangle has two congruent sides (the diagonals) and the hypotenuse (side of the rhombus).
- By the hypotenuse-leg congruence theorem, the four sides of the rhombus are congruent.
Conclusion:
- We have shown that all four angles of the rhombus are right angles and all four sides are congruent.
- By definition, a quadrilateral with four right angles and congruent sides is a square.
- Therefore, a rhombus inscribed in a circle is a square.

|
Explore Courses for Class 9 exam
|

|
Question Description
Prove that the Rhombus inscribed in a circle is a square? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Prove that the Rhombus inscribed in a circle is a square? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prove that the Rhombus inscribed in a circle is a square?.
Prove that the Rhombus inscribed in a circle is a square? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Prove that the Rhombus inscribed in a circle is a square? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prove that the Rhombus inscribed in a circle is a square?.
Solutions for Prove that the Rhombus inscribed in a circle is a square? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of Prove that the Rhombus inscribed in a circle is a square? defined & explained in the simplest way possible. Besides giving the explanation of
Prove that the Rhombus inscribed in a circle is a square?, a detailed solution for Prove that the Rhombus inscribed in a circle is a square? has been provided alongside types of Prove that the Rhombus inscribed in a circle is a square? theory, EduRev gives you an
ample number of questions to practice Prove that the Rhombus inscribed in a circle is a square? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















