Class 11 Exam > Class 11 Questions > Any periodic function can be expressed as a.a...
Start Learning for Free
Any periodic function can be expressed as a.
- a)superposition of sine and cosine functions of different time periods with suitable coefficients
- b)superposition of exponential functions of real time periods with suitable coefficients
- c)superposition of polynomial functions of different time periods with suitable coefficients
- d)superposition of sine and cosine functions of same time period with suitable coefficients
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Any periodic function can be expressed as a.a)superposition of sine an...
All periodic functions can, in principle, be represented as a sum of sine and cosine functions, since they form what's known as a complete set.But in practice, it may be easier to use another type of periodic function. For example, if you try to represent a square wave in terms of sine waves, you run into a problem called the Gibbs phenomenon. The more sine waves you use, the more 'spiked' the edges of the square wave are. This leads to distortions in periodic functions that are 'square-wave-like'.
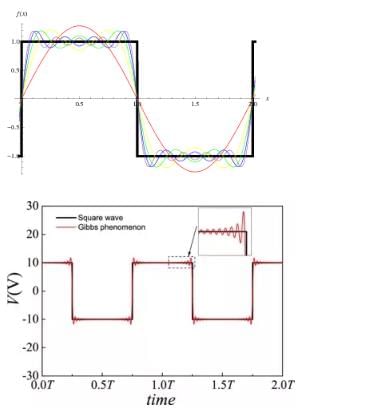
The solution is to instead represent the function in terms of square waves of different periods, or some other function like a triangle or sawtooth wave.
Most Upvoted Answer
Any periodic function can be expressed as a.a)superposition of sine an...
Explanation:
A periodic function is a function that repeats its values in regular intervals. It can be expressed as a superposition of sine and cosine functions of different time periods with suitable coefficients. Let's break down each part of the statement to understand why option 'A' is the correct answer.
Periodic Function:
A periodic function is a function that repeats its values after a certain time period. This means that for any value of x, the function value at x + T is the same as the value at x, where T is the time period.
Sine and Cosine Functions:
Sine and cosine functions are trigonometric functions that oscillate between -1 and 1 as the input varies. They have a periodicity of 2π, which means they repeat their values every 2π units. The sine function has an initial value of 0 at x = 0, while the cosine function has an initial value of 1 at x = 0.
Superposition:
The superposition principle states that the sum of any two or more functions can be expressed as a single function. In the case of periodic functions, we can express them as a superposition of sine and cosine functions.
Representation of Periodic Function:
Any periodic function f(x) can be represented as:
f(x) = a₀/2 + ∑(aₙcos(nx) + bₙsin(nx))
where a₀, aₙ, and bₙ are coefficients, and n is a positive integer representing the harmonic number.
Explanation of Option 'A':
Option 'A' states that any periodic function can be expressed as a superposition of sine and cosine functions of different time periods with suitable coefficients. This aligns with the representation of periodic functions mentioned above, where the function is expressed as a sum of cosine and sine terms.
By adjusting the coefficients aₙ and bₙ, we can determine the amplitudes and phases of each harmonic in the function. This allows us to match the periodic function's shape and characteristics by choosing the appropriate coefficients for each harmonic.
Therefore, option 'A' is the correct answer as it accurately describes the representation of a periodic function as a superposition of sine and cosine functions with suitable coefficients.
Free Test
FREE
| Start Free Test |
Community Answer
Any periodic function can be expressed as a.a)superposition of sine an...
All periodic functions can, in principle, be represented as a sum of sine and cosine functions, since they form what's known as a complete set.
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.
|
Explore Courses for Class 11 exam
|
|
Similar Class 11 Doubts
Top Courses for Class 11View all
Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer?
Question Description
Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer?.
Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Any periodic function can be expressed as a.a)superposition of sine and cosine functions of different time periods with suitable coefficientsb)superposition of exponential functions of real time periods with suitable coefficientsc)superposition of polynomial functions of different time periods with suitable coefficientsd)superposition of sine and cosine functions of same time period with suitable coefficientsCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Class 11 tests.
|
|
Explore Courses for Class 11 exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup