Class 12 Exam > Class 12 Questions > A person is standing in a room of width 200 c...
Start Learning for Free
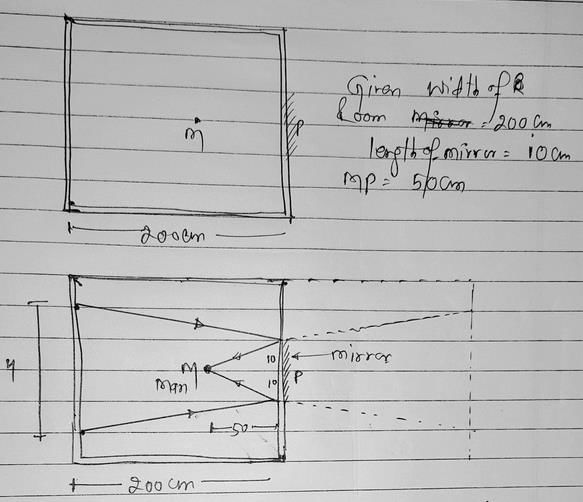
A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)
- a)30 cm
- b)40 cm
- c)50 cm
- d)None
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A person is standing in a room of width 200 cm. A plane mirror of vert...
Ans.
View all questions of this test


Most Upvoted Answer
A person is standing in a room of width 200 cm. A plane mirror of vert...
Given data:
Width of the room = 200 cm
Vertical length of the plane mirror = 10 cm
Distance of the person from the mirror = 50 cm
To find:
The width (height) of the wall behind him that he will be able to see.
Solution:
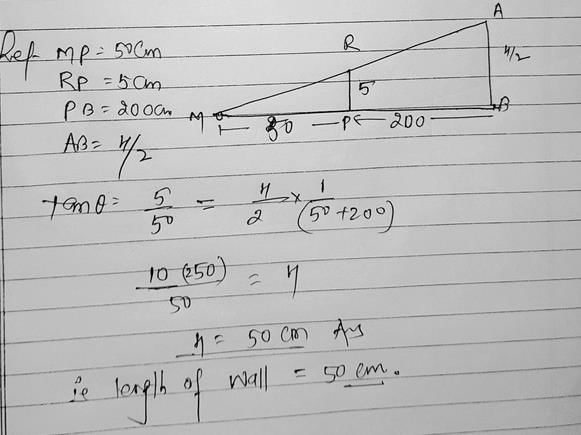
Let AB be the plane mirror fixed on the wall.
Let C be the person standing in front of the mirror.
Draw the perpendicular CD from C to AB.
Let the width of the wall behind the person be EF.
So, we need to find the value of EF.
We know that the angle of incidence is equal to the angle of reflection.
So, the image of the person in the mirror is formed at E.
Join CE.
Now, we have two right triangles ACD and BCE.
Using the concept of similar triangles, we can write:
AC/BC = CD/CE
AC + BC = 50 cm (Given)
AC/BC = CD/CE = 1/10 (Vertical length of the mirror is 10 cm)
On solving, we get:
AC = 5 cm and BC = 45 cm
Using Pythagoras theorem in triangle BCE, we get:
BE^2 + CE^2 = BC^2
BE^2 + (CD + DE)^2 = 45^2
BE^2 + (5 + DE)^2 = 2025
Using Pythagoras theorem in triangle CDE, we get:
DE^2 + CD^2 = CE^2
DE^2 + 50^2 = CE^2
Adding both equations, we get:
BE^2 + DE^2 + (5 + DE)^2 + 50^2 = 2025 + 2025
BE^2 + DE^2 + 10DE + 2525 = 4050
BE^2 + DE^2 + 10DE - 1525 = 0
Now, we know that the image of the person is formed at point E.
So, the width of the wall behind him that he will be able to see is equal to the distance between the points E and F.
Let the distance between E and F be x cm.
Using Pythagoras theorem in triangle DEF, we get:
DE^2 + EF^2 = DF^2
DE^2 + x^2 = (BE + BC)^2
DE^2 + x^2 = 50^2
x^2 = 2500 - DE^2
Substituting the value of DE^2 from the previous equation, we get:
x^2 = 2500 - BE^2 - DE^2 - 10DE
x^2 = 2500 - BE^2 - DE^2 - 10DE + 1525
x^2 = 4025 - BE^2 - DE^2 - 10DE
x^2 = 4025 - 2025
x^2 = 2000
x = √2000
x = 20√5
Therefore, the width (height) of the wall behind him that he will be able to see is 20√5 cm, which is approximately 44.7 cm (rounded to one decimal place).
Hence, the correct option is (c) 50 cm.
Width of the room = 200 cm
Vertical length of the plane mirror = 10 cm
Distance of the person from the mirror = 50 cm
To find:
The width (height) of the wall behind him that he will be able to see.
Solution:
Let AB be the plane mirror fixed on the wall.
Let C be the person standing in front of the mirror.
Draw the perpendicular CD from C to AB.
Let the width of the wall behind the person be EF.
So, we need to find the value of EF.
We know that the angle of incidence is equal to the angle of reflection.
So, the image of the person in the mirror is formed at E.
Join CE.
Now, we have two right triangles ACD and BCE.
Using the concept of similar triangles, we can write:
AC/BC = CD/CE
AC + BC = 50 cm (Given)
AC/BC = CD/CE = 1/10 (Vertical length of the mirror is 10 cm)
On solving, we get:
AC = 5 cm and BC = 45 cm
Using Pythagoras theorem in triangle BCE, we get:
BE^2 + CE^2 = BC^2
BE^2 + (CD + DE)^2 = 45^2
BE^2 + (5 + DE)^2 = 2025
Using Pythagoras theorem in triangle CDE, we get:
DE^2 + CD^2 = CE^2
DE^2 + 50^2 = CE^2
Adding both equations, we get:
BE^2 + DE^2 + (5 + DE)^2 + 50^2 = 2025 + 2025
BE^2 + DE^2 + 10DE + 2525 = 4050
BE^2 + DE^2 + 10DE - 1525 = 0
Now, we know that the image of the person is formed at point E.
So, the width of the wall behind him that he will be able to see is equal to the distance between the points E and F.
Let the distance between E and F be x cm.
Using Pythagoras theorem in triangle DEF, we get:
DE^2 + EF^2 = DF^2
DE^2 + x^2 = (BE + BC)^2
DE^2 + x^2 = 50^2
x^2 = 2500 - DE^2
Substituting the value of DE^2 from the previous equation, we get:
x^2 = 2500 - BE^2 - DE^2 - 10DE
x^2 = 2500 - BE^2 - DE^2 - 10DE + 1525
x^2 = 4025 - BE^2 - DE^2 - 10DE
x^2 = 4025 - 2025
x^2 = 2000
x = √2000
x = 20√5
Therefore, the width (height) of the wall behind him that he will be able to see is 20√5 cm, which is approximately 44.7 cm (rounded to one decimal place).
Hence, the correct option is (c) 50 cm.

|
Explore Courses for Class 12 exam
|

|
Question Description
A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer?.
A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A person is standing in a room of width 200 cm. A plane mirror of vertical length 10 cm is fixed on a wall in front of the person. The person looks into the mirror from distance 50 cm. How much width (height) of the wall behind him will he be able to see : (assume that he uses the full mirror)a)30 cmb)40 cmc)50 cmd)NoneCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















