Class 11 Exam > Class 11 Questions > You hang a flood lamp from the end of a verti...
Start Learning for Free
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?
- a)0.065 mm
- b)0.055 mm
- c)0.045 mm
- d)0.075 mm
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
You hang a flood lamp from the end of a vertical steel wire. The flood...
Given:
- The flood lamp stretches the wire by 0.18 mm
- The stress is proportional to the strain
To find:
- How much would it have stretched if the wire had the same length but twice the diameter
Let's begin by understanding the given information.
Stress is defined as the force per unit area and is denoted by the symbol σ (sigma). Mathematically, stress is given by:
σ = F / A
where F is the force applied and A is the area over which the force is applied.
Strain is defined as the change in length per unit length and is denoted by the symbol ε (epsilon). Mathematically, strain is given by:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the stress is proportional to the strain. This can be expressed mathematically as:
σ ∝ ε
or
σ = kε
where k is a constant of proportionality.
Now, let's apply this information to the problem at hand.
When the flood lamp is hung from the wire, it exerts a force on the wire which causes it to stretch. Let's assume that the original diameter of the wire is d and the original length is L.
From the given information, we know that the stress is proportional to the strain. Therefore, we can write:
σ = kε
where σ is the stress, k is a constant of proportionality, and ε is the strain.
The stress can be calculated using the formula:
σ = F / A
where F is the force applied and A is the cross-sectional area of the wire.
The force applied is the weight of the flood lamp, which can be calculated using the formula:
F = mg
where m is the mass of the flood lamp and g is the acceleration due to gravity.
The cross-sectional area of the wire can be calculated using the formula:
A = πd^2 / 4
where d is the diameter of the wire.
Therefore, we can write:
σ = (mg) / (πd^2 / 4)
The strain can be calculated using the formula:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the flood lamp stretches the wire by 0.18 mm. Therefore, we can write:
ε = 0.18 / L
Now, let's combine the equations for stress and strain:
σ = kε
σ = (mg) / (πd^2 / 4)
ε = 0.18 / L
Substituting the values of σ and ε, we get:
(mg) / (πd^2 / 4) = k (0.18 / L)
Simplifying, we get:
k = (mgL) / (0.18πd^2)
Now, let's use this value of k to calculate the change in length when the diameter of the wire is doubled.
When the diameter of the wire is doubled, the cross-sectional area of the wire becomes 4 times the original area. Therefore, the new diameter is 2d and the new cross-sectional area is:
A' = π(2d)^2 / 4 = 4πd^2
Using the same formula for stress,
- The flood lamp stretches the wire by 0.18 mm
- The stress is proportional to the strain
To find:
- How much would it have stretched if the wire had the same length but twice the diameter
Let's begin by understanding the given information.
Stress is defined as the force per unit area and is denoted by the symbol σ (sigma). Mathematically, stress is given by:
σ = F / A
where F is the force applied and A is the area over which the force is applied.
Strain is defined as the change in length per unit length and is denoted by the symbol ε (epsilon). Mathematically, strain is given by:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the stress is proportional to the strain. This can be expressed mathematically as:
σ ∝ ε
or
σ = kε
where k is a constant of proportionality.
Now, let's apply this information to the problem at hand.
When the flood lamp is hung from the wire, it exerts a force on the wire which causes it to stretch. Let's assume that the original diameter of the wire is d and the original length is L.
From the given information, we know that the stress is proportional to the strain. Therefore, we can write:
σ = kε
where σ is the stress, k is a constant of proportionality, and ε is the strain.
The stress can be calculated using the formula:
σ = F / A
where F is the force applied and A is the cross-sectional area of the wire.
The force applied is the weight of the flood lamp, which can be calculated using the formula:
F = mg
where m is the mass of the flood lamp and g is the acceleration due to gravity.
The cross-sectional area of the wire can be calculated using the formula:
A = πd^2 / 4
where d is the diameter of the wire.
Therefore, we can write:
σ = (mg) / (πd^2 / 4)
The strain can be calculated using the formula:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the flood lamp stretches the wire by 0.18 mm. Therefore, we can write:
ε = 0.18 / L
Now, let's combine the equations for stress and strain:
σ = kε
σ = (mg) / (πd^2 / 4)
ε = 0.18 / L
Substituting the values of σ and ε, we get:
(mg) / (πd^2 / 4) = k (0.18 / L)
Simplifying, we get:
k = (mgL) / (0.18πd^2)
Now, let's use this value of k to calculate the change in length when the diameter of the wire is doubled.
When the diameter of the wire is doubled, the cross-sectional area of the wire becomes 4 times the original area. Therefore, the new diameter is 2d and the new cross-sectional area is:
A' = π(2d)^2 / 4 = 4πd^2
Using the same formula for stress,
Free Test
FREE
| Start Free Test |
Community Answer
You hang a flood lamp from the end of a vertical steel wire. The flood...
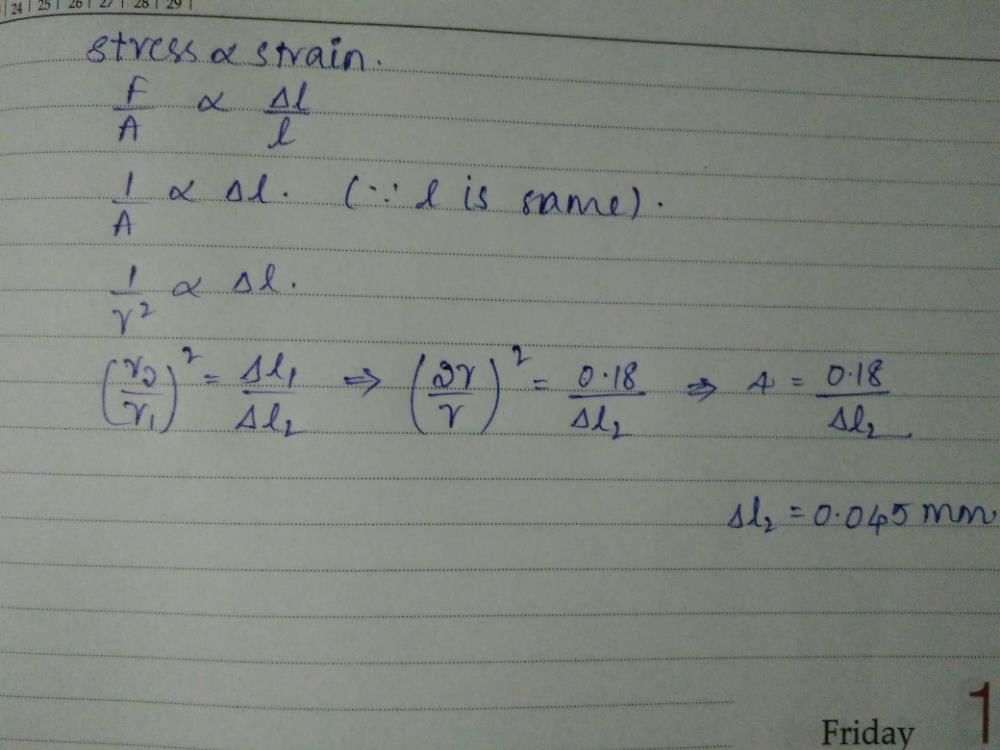

|
Explore Courses for Class 11 exam
|

|
Question Description
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer?.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer?.
Solutions for You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?a)0.065 mmb)0.055 mmc)0.045 mmd)0.075 mmCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























