Class 12 Exam > Class 12 Questions > A beam of natural light falls on a system of ...
Start Learning for Free
A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256?
Most Upvoted Answer
A beam of natural light falls on a system of 5 polaroids which are arr...
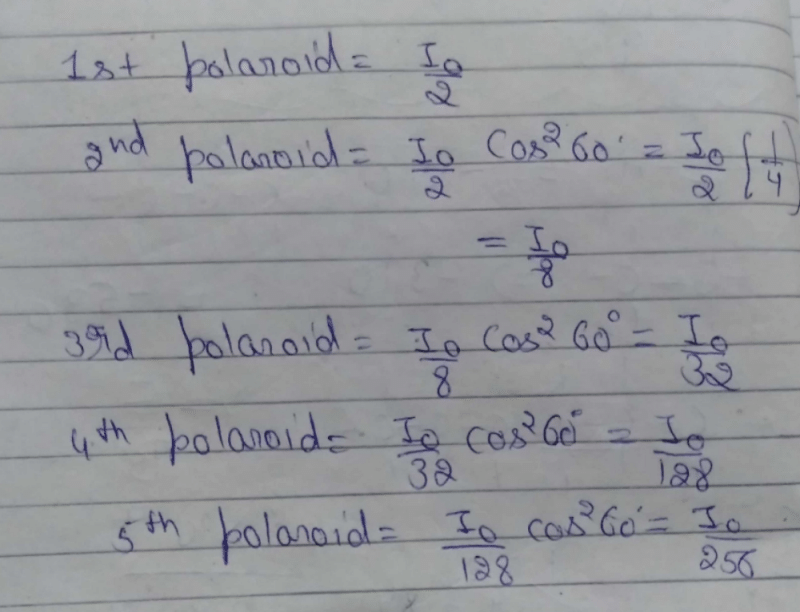
Community Answer
A beam of natural light falls on a system of 5 polaroids which are arr...
The given system consists of 5 polaroids arranged in succession, with the transmission axes of each polaroid turned through 60 degrees with respect to the preceding one. We need to determine the fraction of incident light intensity that passes through the system.
Let's analyze the system step by step:
1. **First Polaroid**: When unpolarized light falls on the first polaroid, it allows only the light vibrating in a particular plane to pass through. Since the transmission axis of the first polaroid is arbitrary, it lets half of the incident light intensity to pass through. Therefore, the intensity of light passing through the first polaroid is 1/2.
2. **Second Polaroid**: The light coming out of the first polaroid is now linearly polarized in a particular direction. When it falls on the second polaroid, which is oriented 60 degrees with respect to the first one, only the component of light vibrating in a direction parallel to the transmission axis of the second polaroid will pass through. The projection of the linearly polarized light along the transmission axis of the second polaroid is given by cos^2(60). Hence, the intensity of light passing through the second polaroid is (cos^2(60)) * (1/2) = 1/4.
3. **Third Polaroid**: Similarly, the light coming out of the second polaroid is linearly polarized in a particular direction. When it falls on the third polaroid, which is oriented 60 degrees with respect to the second one, only the component of light vibrating in a direction parallel to the transmission axis of the third polaroid will pass through. The projection of the linearly polarized light along the transmission axis of the third polaroid is again given by cos^2(60). Hence, the intensity of light passing through the third polaroid is (cos^2(60)) * (1/4) = 1/8.
4. **Fourth Polaroid**: The same process repeats for the fourth polaroid, and the intensity of light passing through it is (cos^2(60)) * (1/8) = 1/16.
5. **Fifth Polaroid**: Finally, when the light falls on the fifth polaroid, which is oriented 60 degrees with respect to the fourth one, only the component of light vibrating in a direction parallel to the transmission axis of the fifth polaroid will pass through. The projection of the linearly polarized light along the transmission axis of the fifth polaroid is once again given by cos^2(60). Hence, the intensity of light passing through the fifth polaroid is (cos^2(60)) * (1/16) = 1/32.
Therefore, the fraction of incident light intensity that passes through the system is 1/32.
Hence, the correct answer is option 1) 1/32.
Let's analyze the system step by step:
1. **First Polaroid**: When unpolarized light falls on the first polaroid, it allows only the light vibrating in a particular plane to pass through. Since the transmission axis of the first polaroid is arbitrary, it lets half of the incident light intensity to pass through. Therefore, the intensity of light passing through the first polaroid is 1/2.
2. **Second Polaroid**: The light coming out of the first polaroid is now linearly polarized in a particular direction. When it falls on the second polaroid, which is oriented 60 degrees with respect to the first one, only the component of light vibrating in a direction parallel to the transmission axis of the second polaroid will pass through. The projection of the linearly polarized light along the transmission axis of the second polaroid is given by cos^2(60). Hence, the intensity of light passing through the second polaroid is (cos^2(60)) * (1/2) = 1/4.
3. **Third Polaroid**: Similarly, the light coming out of the second polaroid is linearly polarized in a particular direction. When it falls on the third polaroid, which is oriented 60 degrees with respect to the second one, only the component of light vibrating in a direction parallel to the transmission axis of the third polaroid will pass through. The projection of the linearly polarized light along the transmission axis of the third polaroid is again given by cos^2(60). Hence, the intensity of light passing through the third polaroid is (cos^2(60)) * (1/4) = 1/8.
4. **Fourth Polaroid**: The same process repeats for the fourth polaroid, and the intensity of light passing through it is (cos^2(60)) * (1/8) = 1/16.
5. **Fifth Polaroid**: Finally, when the light falls on the fifth polaroid, which is oriented 60 degrees with respect to the fourth one, only the component of light vibrating in a direction parallel to the transmission axis of the fifth polaroid will pass through. The projection of the linearly polarized light along the transmission axis of the fifth polaroid is once again given by cos^2(60). Hence, the intensity of light passing through the fifth polaroid is (cos^2(60)) * (1/16) = 1/32.
Therefore, the fraction of incident light intensity that passes through the system is 1/32.
Hence, the correct answer is option 1) 1/32.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256?
Question Description
A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256?.
A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256?.
Solutions for A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? defined & explained in the simplest way possible. Besides giving the explanation of
A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256?, a detailed solution for A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? has been provided alongside types of A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? theory, EduRev gives you an
ample number of questions to practice A beam of natural light falls on a system of 5 polaroids which are arranged in success such that the past axis of each polaroid is turn through 60 degree w.r.t.the preceding one the fraction of incident light intensity that passes through the system is 1)1/32 2)1/512 3)1/128 4)1/256? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















