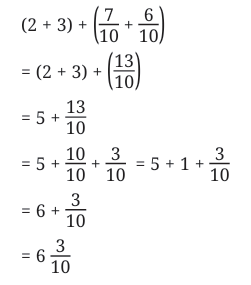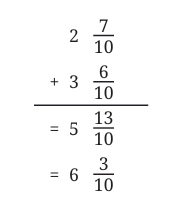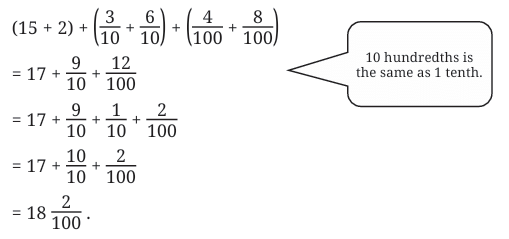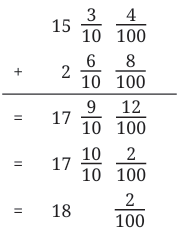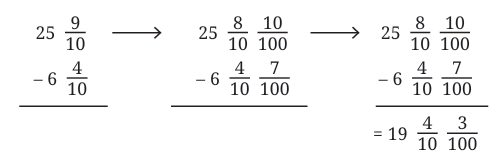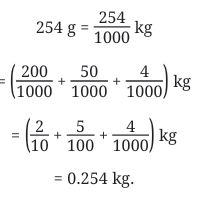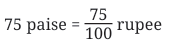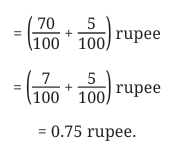A Peek Beyond the Point Class 7 Notes Maths Chapter 3 Free PDF
The Need for Smaller Units
Have you ever tried to fix something, maybe a toy or a small gadget, and found that a tiny screw just wouldn't fit? That's exactly what happened to Sonu one day!
- He was watching his mother trying to fix his favourite toy car. She had a small screw, but it just wasn't the right size to join two pieces together.
- Sonu watched with wide eyes, full of curiosity. Why wouldn't it work?
 Sonu's mother trying to fix his toy with small screw
Sonu's mother trying to fix his toy with small screw
- His mother explained, "This screw isn't quite the right size, Sonu." She rummaged through her toolbox and found another screw.
- This time, it worked perfectly, and the toy was fixed! To Sonu, both screws looked almost exactly the same. He picked them up and looked very, very closely.
- Ah! He could see it now – one screw was just a tiny bit longer than the other.
 Yes, one screw was bit longer than the other
Yes, one screw was bit longer than the other - Sonu was amazed. How could such a small, almost invisible difference in length make such a big difference in fixing his toy?
- He became really curious. How much longer was one screw than the other?
- And how could he even measure such a tiny difference when they looked so similar?
This little adventure with the screws got Sonu thinking about measurement. Sometimes, just saying something is 'long' or 'short' isn't enough. We need to know exactly how long or short it is.
Measuring with Greater Precision
Look at the screws below placed on different rulers. Can you see how the bottom ruler, with more marks, helps us measure more accurately?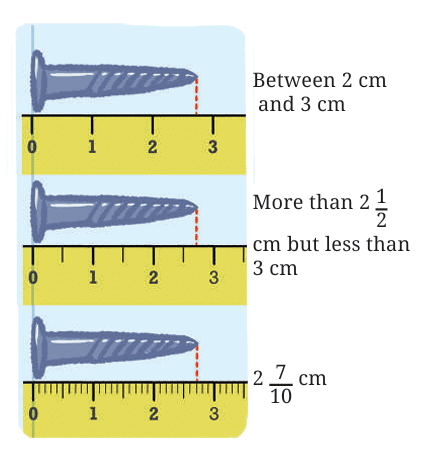 Screws placed on different Ruler to measure the length
Screws placed on different Ruler to measure the length
- Look at the top ruler first. It only has markings for whole centimeters (cm). Using this ruler, we can only say that both screws are between 2 cm and 3 cm long. That's not very helpful when we need to know which one is longer!
- Now look at the middle ruler. This one has more markings - it divides each centimeter into 10 equal parts. With this ruler, we can be more precise. The first screw measures 2 7/10 cm (or 2.7 cm). That means it's 2 whole centimeters plus 7 tenths of a centimeter.
- The bottom ruler is even more detailed. It divides each centimeter into many tiny parts, allowing for even more precise measurements.
A Tenth Part
Have you ever wondered how we can measure things more precisely? Let's explore this with a simple example.
Look at the pencil shown in the figure below:
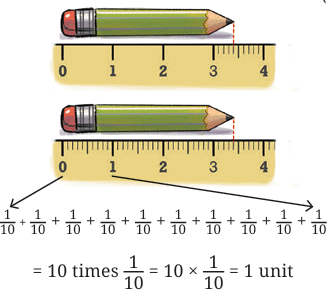
Notice how the pencil's length isn't exactly 3 units or 4 units. It's somewhere in between. When we look at the ruler with more detailed markings (the bottom one), we can see that the pencil measures 3 and 4 tenths of a unit, which we write as 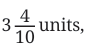
But what does 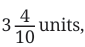 actually mean? Let's break it down:
actually mean? Let's break it down:
3 represents the whole units (3 × 1)
4/10 represents four one-tenths (4 × 1/10)
So the total length is (3 × 1) + (4 × 1/10) units.
This length is the same as 34 one-tenths units because 10 one-tenths units make one unit.
There are different ways to express measurements with tenths:
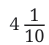 is read as "four and one-tenth"
is read as "four and one-tenth"4/10 is read as "four-tenths"
41/10 is read as "forty-one tenths"
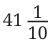 is read as "forty-one and one-tenth"
is read as "forty-one and one-tenth"
Example 1: Sonu was measuring parts of his arm. The length of his lower arm was 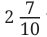 units, and his upper arm was
units, and his upper arm was 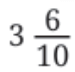 units. What is the total length of his arm?
units. What is the total length of his arm?
Sol: To find the total length, we need to add the measurements:
Method 1:
Lower arm: 2 units and 7 tenths
Upper arm: 3 units and 6 tenths
Total units: 2 + 3 = 5 units
Total tenths: 7 + 6 = 13 tenths
But 13 tenths equals 1 unit and 3 tenths (since 10 tenths = 1 unit).
So the total length is 5 + 1 + 3/10 =
units.
Method 2:
We can convert both measurements to tenths and then add:
So Sonu's complete arm measures
units long.
A Hundredth Part
We learned about tenths, which help us measure more precisely than whole units. But what if we need to be even more precise? Let's explore!
- Imagine you have a sheet of paper that measures 8 whole 9/10 units long. That's 8 whole units and 9 tenths of a unit.
- Now, what happens if you fold this paper exactly in half along its length? What would the new length be?
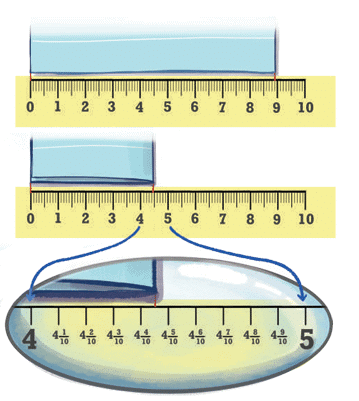
If we try to measure the folded paper using a ruler marked only in tenths, we might find that the length falls between two tenth markings. For example, it might be between 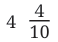 and
and 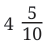 units. We can estimate, but we can't get an exact measurement with just tenths.
units. We can estimate, but we can't get an exact measurement with just tenths.
Introducing Hundredths
To measure even smaller lengths, we can do something similar to what we did before: we can divide each tenth into 10 smaller, equal parts.
Think about it:
1 unit is divided into 10 tenths.
Each tenth is divided into 10 smaller parts.
So, how many of these tiny parts make up one whole unit? That's right!
10 tenths × 10 parts per tenth = 100 parts.
Each of these tiny parts is called one-hundredth (1/100) of the unit.
Measuring with Hundredths
Now, let's go back to our folded paper. Using a ruler with hundredth markings, we can measure its length much more accurately. Let's say the folded edge lands exactly on the 5th small mark after  .
.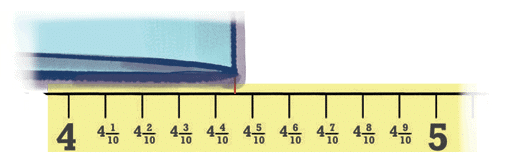
We can express this length in a few ways:
4 units, 4 tenths, and 5 hundredths: 4 + 4/10 + 5/100
4 units and 45 hundredths: 4 + 45/100 (since 4 tenths = 40 hundredths, so 40/100 + 5/100 = 45/100)
Reading and Writing Hundredths
Just like with tenths, we have different ways to read and write measurements involving hundredths:

These all represent the same length!
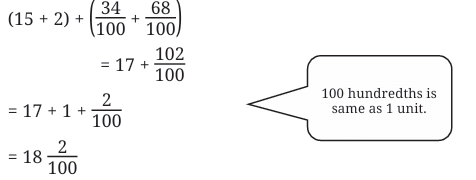
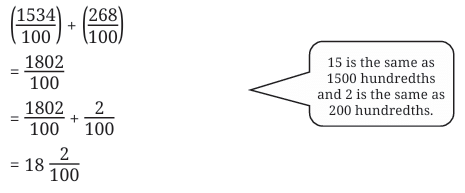
Example 2: What is the sum of 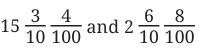 ?
?
Sol: Method 1 (Adding units, tenths, hundredths separately):
Method 2 (Converting everything to hundredths):
Method 3:
Method 4:
Example 3: What is the difference: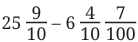 ?
?
Sol:
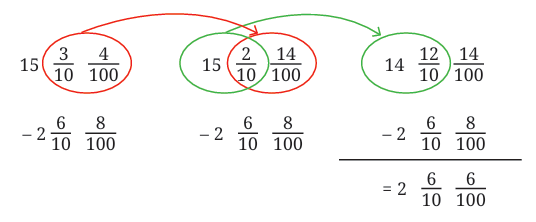
Example 4: What is the difference 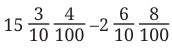 ?
?
Sol:
Decimal Place Value
We've seen how dividing units into tenths and then hundredths helps us measure more precisely. But why do we always divide by 10? Why not 4, or 5, or 8 equal parts?
Yes, we can.
Look at the pencils in the image:
One ruler is marked in tenths (0.1, 0.2, 0.3...)
The other is marked in quarters (¼, ½, ¾...)
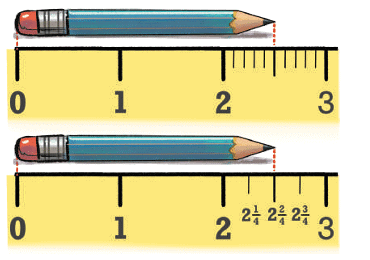
If we split each quarter further into 4 smaller parts, we get sixteenths (1⁄16), which are even more accurate.
So, why do we usually split into 10 parts?
That’s because of our number system – the Indian place value system (and the international system too) is based on 10s.
Each place value is 10 times:
Bigger than the one to its right
Smaller than the one to its left
For example:
10 ones = 1 ten
10 tens = 1 hundred
10 hundreds = 1 thousand
That’s why decimal place values go like:
0.1 = 1⁄10 (one-tenth)
0.01 = 1⁄100 (one-hundredth)
0.001 = 1⁄1000 (one-thousandth)
Notice a pattern?
Each place value is 10 times bigger than the one immediately to its right. Or, looking the other way, each place value is 10 times smaller (or one-tenth) than the one immediately to its left.
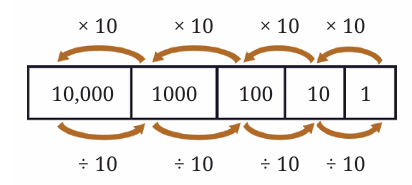
To extend this system to numbers smaller than one, it makes perfect sense to continue this pattern: divide the Ones place by 10!
Dividing 1 by 10 gives one-tenth (1/10).
Dividing one-tenth (1/10) by 10 gives one-hundredth (1/100).
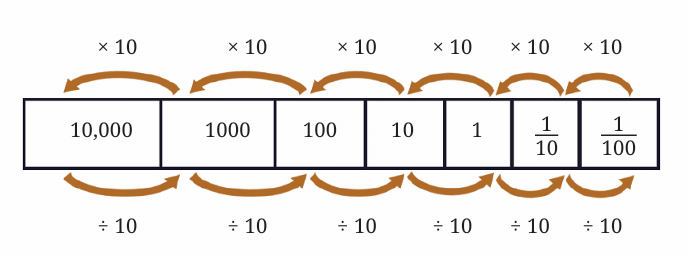
Dividing one-hundredth (1/100) by 10 gives one-thousandth (1/1000).
...and so on!
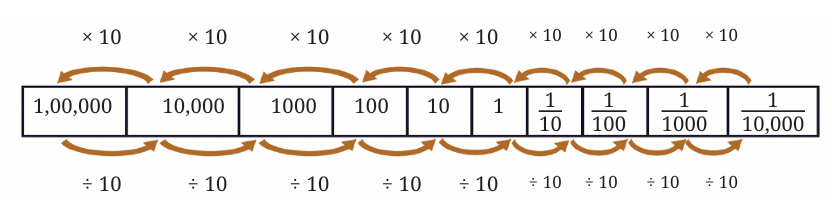
What will the fraction be when 1/ 100 is split into 10 equal parts?
It will be 1/ 1000 , i.e., a thousand such parts make up a unit.
This system, based on the number 10, is called the decimal system.

Notation, Writing and Reading of Numbers
We need a way to clearly separate the whole number part from the fractional part (tenths, hundredths, etc.). If we just wrote 42, how would we know if it means "4 tens and 2 ones" (42) or "4 ones and 2 tenths" (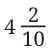 )?
)?
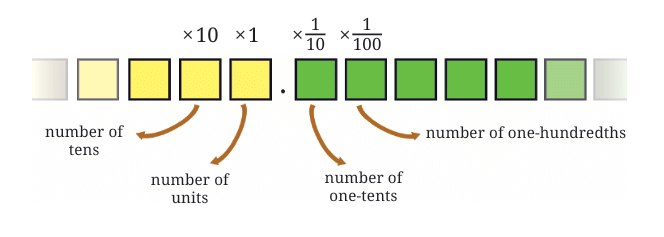
To solve this, we use a special symbol: the decimal point (.) .
It acts as a separator between the Ones place and the Tenths place.
Whole Numbers are to the left of the decimal point.
Fractional Parts (tenths, hundredths, etc.) are to the right of the decimal point.
Let's look at some examples: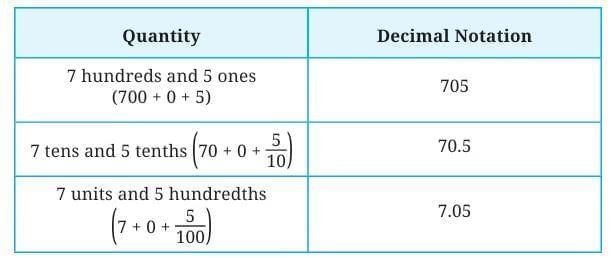
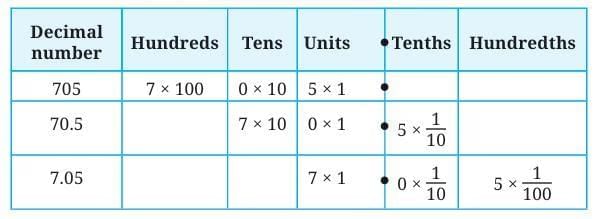
These numbers, when shown through place value, are as follows:
Reading Decimal Numbers
How do we read these numbers aloud?
705: "Seven hundred five" (No decimal part)
70.5: "Seventy point five" (or "Seventy and five tenths")
7.05: "Seven point zero five" (or "Seven and five hundredths")
Important: When reading the digits after the decimal point, we usually say each digit individually (like "point two seven four", not "point two hundred seventy-four"). This helps avoid confusion about place value.
Example 5: How can we write 234 tenths in decimal form?
Sol: 234 tenths = 234/10
We can break this down:
234/10 = (200 + 30 + 4) / 10
= 200/10 + 30/10 + 4/10
= 20 + 3 + 4/10
= 23.4
In decimal notation, this is 23.4.
Units of Measurement
Now that we understand decimal numbers, let's see how they help us work with different units of measurement, especially for length.
Length Conversion: Millimeters (mm) and Centimeters (cm)
You've probably used a ruler marked in centimeters (cm) and millimeters (mm). You might already know that:
⇒ 1 cm = 10 mm
This means that each centimeter is divided into 10 equal parts, and each part is a millimeter.
So, how much of a centimeter is one millimeter?
Since 10 mm make 1 cm, then:
⇒ 1 mm = 1/10 cm
Using our new decimal notation, we can write this as:
⇒ 1 mm = 0.1 cm (one-tenth of a centimeter)
Let's practice converting between mm and cm using decimals:
Q: How many cm is 5 mm?
5 mm = 5/10 cm = 0.5 cm
Q: How many cm is 12 mm?
12 mm = 10 mm + 2 mm
= 1 cm + 2/10 cm
= 1.2 cm
Q: How many mm is 5.6 cm?
5.6 cm = 5 cm and 6/10 cm
= (5 × 10 mm) + (6/10 × 10 mm)
= 50 mm + 6 mm = 56 mm
Length Conversion: Centimeters (cm) and Meters (m)
We also know the relationship between centimeters and meters:
⇒ 1 m = 100 cm
This means one meter is divided into 100 equal parts, and each part is a centimeter. So, how much of a meter is one centimeter?
Since 100 cm make 1 m, then:
⇒ 1 cm = 1/100 m
Using decimal notation:
⇒ 1 cm = 0.01 m (one-hundredth of a meter)

These tiny measurements show how important tenths and hundredths (and even smaller units!) are in science and everyday life.
Weight Conversion
It shows how weights can be expressed in decimal form and why that’s useful in real life.1 kilogram (kg) = 1000 grams (g)
So, 1 gram = 1/1000 kg = 0.001 kg
Q: How many kilograms is 5 g?
5 g = 5 ÷ 1000 = 0.005 kg
Q: How many kilograms is 10 g?
10 g = 10 ÷ 1000 = 0.010 kg
As each gram is one-thousandth of a kg, 254 g can be written as
This can be broken as:
200 g → 0.2 kg
50 g → 0.05 kg
4 g → 0.004 kg
Total = 0.254 kg
Rupee ─ Paise conversion
In India, the currency system is based on rupees and paise.
Basic Conversion Rule:
1 rupee = 100 paise
So, 1 paise = 1/100 rupee = ₹ 0.01
That means if you divide 1 rupee into 100 equal parts, each part is called 1 paise.
Q. How many rupees is 75 paise?
Locating and Comparing Decimals
What are Decimals?
Decimals are numbers that show values smaller than 1. They help us measure things more accurately, like length, weight, and money.
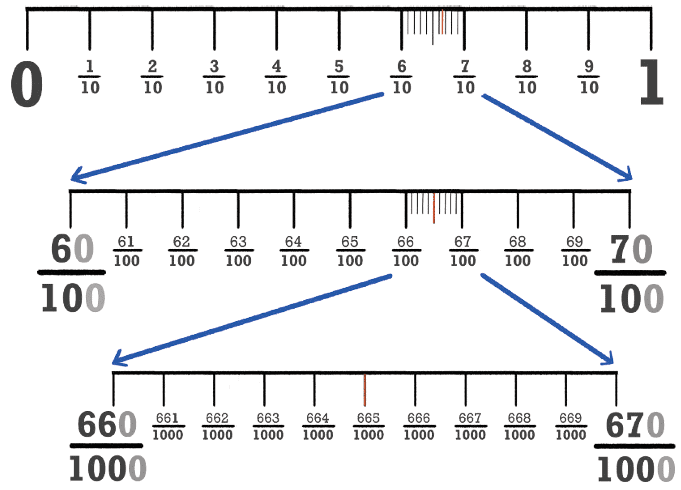
How to Show Decimals on a Number Line?
To place a decimal like 1.4 on a number line:
First, see which two whole numbers it lies between.
1.4 lies between 1 and 2.Then divide the gap between 1 and 2 into 10 equal parts.
The 4th division after 1 is 1.4.

So, 1.4 = 1 unit and 4 tenths.
Does Adding Zeros Change the Value?
Let’s compare:
- 0.2 = 0.20 = 0.200 — All same (2 tenths)
But:
- 0.02 = 2 hundredths
0.002 = 2 thousandths
These are different.
Adding zeros to the right after decimal digits doesn't change the value. But changing the place value (tenths, hundredths, thousandths) does.
Ordering Decimal Numbers
Look at these numbers:
4.5, 4.05, 4.005, 4.050, 4.50
Let’s convert them all to the same format (3 decimal places):
4.500
4.050
4.005
4.050
4.500
Now, it's easier to compare:
Smallest = 4.005
Largest = 4.500
4.5 = 4.50
4.05 = 4.050
Closest Decimals
This concept teaches you how to compare decimal numbers and figure out which decimal is closest to a given number.
Let’s compare the numbers:
0.9, 1.1, 1.01, and 1.11
Which one is closest to 1?
Step 1: Arrange the numbers in order:
0.9 < 1 < 1.01 < 1.1 < 1.11
Step 2: See how far each number is from 1:
0.9 is 0.1 away (10/100)
1.1 is also 0.1 away
1.01 is just 0.01 away (1/100)
So, 1.01 is closest to 1.
This improves your understanding of how place value affects the size of decimal numbers.
Addition and Subtraction of Decimals
This concept teaches how to add and subtract numbers with decimals (like 2.7, 3.5, etc.), just like you do with whole numbers. The only difference is that you have to align the decimal points and work carefully with tenths, hundredths, or thousandths.
Example 6: Priya needs 2.7 m of cloth and Shylaja needs 3.5 m of cloth. How much cloth is needed in total?
Sol: We add:
2.7 + 3.5 = 6.2 mHow?
2.7 = 2 + 7/10
3.5 = 3 + 5/10
Add: (2 + 3) + (7/10 + 5/10) = 5 + 12/10
12/10 = 1 whole and 2/10
Total = 6 + 2/10 = 6.2 m
Example 7: How much longer is Shylaja’s cloth compared to Priya’s?
Sol: We subtract:
3.5 – 2.7 = 0.8 mIn fractions:
3.5 = 3 + 5/10
2.7 = 2 + 7/10
So, difference = 8/10 = 0.8
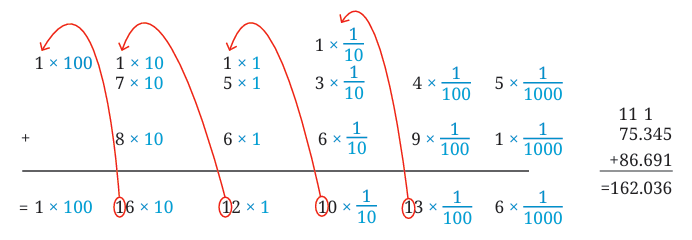
Detailed Decimal Addition (Place Value Style)
Let’s add:
75.345 + 86.691
Each digit is added based on place value:
Decimal Sequences
A sequence is a list of numbers that follow a pattern.
In a decimal sequence, each number includes a decimal point and the numbers change in a regular way.
What is the pattern?
Let’s look at this example:4.4, 4.8, 5.2, 5.6, 6.0...
What’s happening here?
Each number is increasing by 0.4.
So, to continue the sequence, we keep adding 0.4:
6.0 + 0.4 = 6.4
6.4 + 0.4 = 6.8
6.8 + 0.4 = 7.2
The next 3 terms are: 6.4, 6.8, 7.2.
Estimating Sums and Differences
Sometimes, when we add or subtract decimal numbers, we want to quickly estimate the answer before calculating exactly. Estimating helps us check if our final answer is reasonable.
Sonu noticed an interesting pattern and made a smart observation:
“If we add two decimal numbers, the answer will always be more than the sum of their whole number parts, but less than 2 more than that.”
Example:
1. Let’s take the numbers 25.936 and 8.202
Whole number parts: 25 and 8
Their sum is: 25 + 8 = 33
So, Sonu says the final sum should be:
More than 33
Less than 33 + 2 = 35
Let’s check:
Actual sum = 25.936 + 8.202 = 34.138
Yes! It lies between 33 and 35 – so Sonu’s idea works here.
2. Let’s say you want to subtract two decimals, like:
9.6 – 2.3
Whole number parts are 9 and 2
The answer will lie between 9 – 2 = 7 and 9 – 2 + 1 = 8
Actual answer: 7.3, which lies between 7 and 8
Conclusion:
Think of the whole number part first.
Then remember:
For addition: the answer is a little more than just adding the whole numbers.
For subtraction: the answer is a little less than just subtracting the whole numbers.
More on the Decimal System
Decimal numbers use a dot (called the decimal point) to separate the whole part of a number from the fractional part. For example:
1.5 means one and a half
0.05 means five hundredths
Sometimes, small mistakes in placing or reading this decimal point can lead to huge real-world problems which are as follows:
1. Amsterdam’s Money Mistake (2013):
They meant to send €1.8 million.
But due to a decimal error, they sent €188 million.
Why? Because the amount was entered in euro-cents instead of euros (1 euro = 100 cents).
That’s 100 times more money!
2. The Plane Fuel Disaster (1983):
Ground staff gave fuel in pounds instead of kilograms.
The plane had half the fuel it actually needed.
The decimal error could’ve cost lives, but thankfully, everyone survived.
3. Medical Mistakes:
If a doctor reads 0.05 mg as 0.5 mg, that’s 10 times the correct amount.
This could be dangerous when giving medicine.

Deceptive Decimal Notation
1. Decimal Confusion in Time (Deceptive Decimal Notation):
When you see 4.5 hours, don’t think it’s 4 hours and 5 minutes.
0.5 hours actually means 30 minutes, not 5 minutes!
So, 4.5 hours after noon is 4:30 PM, not 4:05 PM.
2. Real-Life Measurement Mistake:
If someone says 2.5 feet, it means 2 feet 6 inches (because 0.5 ft = 6 inches).
But if they actually meant 2 feet 5 inches, the door or object won’t fit correctly.
This shows why it’s important to know what decimals mean in real measurements.

3. Decimal Notation in Sports (Like Cricket):
In cricket, 5.5 overs means 5 overs + 5 balls (because 1 over = 6 balls).
So, 5.5 ≠ 5 overs 50%; it means 5 overs and 5 balls = 5.833 overs in true decimal form!
A Pinch of History – Decimal Notation Over Time
Ancient mathematicians like Shridhara and Abu’l Hassan used fractions like 1/10, 1/100.
In 15th century, people marked decimal parts in different colors or added little superscript numbers (like 3⁶).
In 16th century, John Napier and Christopher Clavius introduced the use of a dot (.) to separate whole numbers and decimals (like 2.5).
Some countries today use comma
 instead of a dot (e.g., 1,000.5 becomes 1.000,5).
instead of a dot (e.g., 1,000.5 becomes 1.000,5).
FAQs on A Peek Beyond the Point Class 7 Notes Maths Chapter 3 Free PDF
| 1. Why is it important to measure with greater precision? |  |
| 2. What are tenths and how do they work in measurements? |  |
| 3. How do you add lengths that include tenths? |  |
| 4. How can I practice measuring with tenths effectively? |  |
| 5. What are some common applications of measuring in tenths? |  |