Class 10 Maths Chapter 2 Question Answers - Polynomials
Q 1. How many zeroes can the polynomial 2x2 - 3x + 4 have?
It is a quadratic polynomial i.e. the degree of 2x2 - 3x + 4 is 2.
∴ It can have two zeroes at the most.
Q 2. The graph of y = p (x) is shown in the figure below. How many zeroes does p (x) have?
Since the curve (graph) of p (x) is intersecting the x-axis at three points,
∴ y = p (x) has 3 zeroes.
Q 3. What is the value of p (x) = x2 - 3x - 4 at x = 2?
Given,
p(x) = x2 - 3x - 4
⇒ p(2) = (2)2 - 3 (2) - 4
⇒ 4 - 6 - 4 = - 6
Q 4. What is the value of p (x) = x2 - 3x - 4 at x = - 1?
We have,
p(x) = x2 - 3x - 4
⇒ p (- 1) = (- 1)2 - {3 (- 1)} - 4
⇒ 1 + 3 - 4 = 0
Q 5. What is the zero of 2x + 3?
Since,
The zero of a linear polynomial = - Constant termCoefficient of x
∴ The zero of 2x + 3 = -3/2
Q 6. The Coefficient of x and the constant term in a linear polynomial are 5 and - 3 respectively. Find its zero.
Since,
The zero of a linear polynomial = - Constant termCoefficient of x
∴ The zero of the given linear polynomial= - -35 = 35
Q 7. The graph of a quadratic polynomial x2 - 3x - 4 is a parabola. Determine the opening of the parabola.
In x2 - 3x - 4, the Coefficient of x2 is 1 and 1 > 0
∴ The parabola opens upwards.
Q 8. Find the sum of the zeroes of the polynomial 2x2 - 8x + 6.
p (x) = x2 - 3x - 4
p (x) = 2x2 - 8x + 6
∴ a = 2, b = - 8 and c = 6
⇒ Sum of the zeroes = -b/a
⇒ -(-8)/(2) = 4
Q 9. Find the product of zeroes of the quadratic polynomial 3x2 + 5x - 2.
Here, a = 3, b = 5 and c = - 2
As, Product of the zeroes = c/a
⇒ Product of the zeroes of 3x2 + 5x - 2 = -2/3
Q 10. If a fifth degree polynomial is divided by a quadratic polynomial, write the possible degree of the quotient.
∵ Degree of the dividend p(x) = 5
Degree of the divisor f(x) = 2
∴ Degree of the quotient q(x) = Degree of p(x) - Degree of f(x) = 5 - 2 = 3
Q 11. Graph of a linear polynomial is a straight line. If the points (0, 4), (1, 2) and (2, 0) lie on this graph, write the zero of the polynomial.
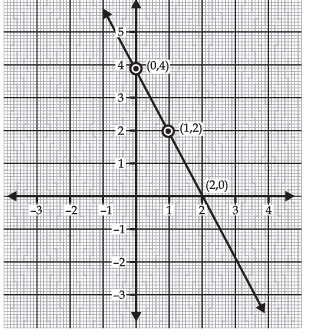
y = p (x) has its zero at a point where y = 0
In the figure, y = 0 at (2, 0).
∴ 2 is the zero of p (x).
Q 12. For what value of k, (- 4) is a zero of the polynomial x2 - x - (2k + 2)?
Since, (- 4) is the zero of p (x)
⇒ p (- 4) = (- 4)2 - (- 4) - (2k + 2) = 0
⇒ 16 + 4 = 2k + 2
⇒ 20 - 2 = 2k
⇒ 18= 2k
⇒ k = 18/2 = 9
Thus, the required value of k = 9.
Q 13. For what value of p, (- 4) is a zero of the polynomial x2 - 2x - (7p + 3)?
We have
∵ p (x) = x2 - 2x - (7p + 3)
p (- 4) = (- 4)2 - 2 (- 4) - (7p + 3)
Since - 4 is a zero of p (x),
∴ (- 4)2 - 2 (- 4) - (7p + 3) = 0
⇒ 16 + 8 = 7p + 3
⇒ 24 - 3 = 7p
⇒ 7p = 21
⇒ p = 21/7= 3
Thus, the required value of p is 3.
Q 14. The sum and product of the zeroes of a quadratic polynomial are 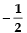 and - 3 respectively. What is the quadratic polynomial?
and - 3 respectively. What is the quadratic polynomial?
For a quadratic polynomial, we have
Sum of zeroes = -1/2Product of the zeroes = -3
Since general equation of the quadratic polynomial
= x2 - [Sum of the roots] x + [Product of the roots]
⇒ ⇒ x2 -[ -12]x + [-3] = x2 + 12 x - 3
Q 15. The graph of y = f (x) is given in the figure, find the number of zeroes of f (x).
From the figure (graph), it is evident that y = f (x) intersects the x-axis at two distinct points A and B.
∴ Number of zeroes of f (x) = 2.
Q 16. In the adjoining figure the graph of a polynomial p (x) is given. Find the zeroes of the polynomial.
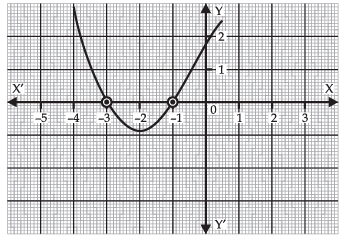
From the graph, it is evident that the graph of the given polynomial intersects the x-axis at - 1 and - 3.
∴ The zeroes of the polynomial are - 1 and - 3.
Q 17. If 1 is a zero of the polynomial p (x) = ax2 - 3 (a - 1) x - 1, then find the value of a.
Here, p (x) = ax2 - 3(a - 1)x - 1
∴ p(1) = a(1)2 - 3(a - 1) × 1 - 1
= a - 3a + 3 - 1
= - 2a + 2
∵ 1 is a zero of p (x);
∴ p (1) = 0
⇒ - 2a + 2 = 0 ⇒ a = 1
Q 18. If (x + a) is a factor of 2x2 + 2ax + 5x + 10 find a.
Here, p(x) = 2x2 + 2ax + 5x + 10
∵ (x + a) is a factor of p(x)
∴ - a is a zero of p(x)
⇒ p (- a) = 0
⇒ 2 (- a)2 + 2a (- a) + 5 (- a) + 10 = 0
⇒ 2a2 - 2a2 - 5a + 10 = 0
⇒ a = 10/5 = 2
Thus, the required value of a = 2.
Q 19. Write the zeroes of the polynomial x2 + 2x + 1.
We have,
p (x) = x2 + 2x + 1
= (x + 1)2
If p (x) = 0 then (x + 1)2 = 0
⇒ x = - 1
Thus, the zero of the polynomial p (x) is - 1.
Q 20. Write the zeroes of the polynomial x2 - x - 6.
We have,
p (x) = x2 - x - 6
= x2 - 3x + 2x - 6
⇒ x (x - 3) + 2 (x - 3)
⇒ (x - 3) (x + 2)
For p (x) = 0
⇒ (x - 3) (x + 2) = 0
∴ x = 3 and x = - 2
Q 21. Write a quadratic polynomial, the sum and product of whose zeroes are 3 and - 2 respectively.
A quadratic polynomial is given by
x2 - [Sum of the zeroes] x + [Product of zeroes]
But, Sum of zeroes = 3
Product of zeroes = - 2
∴ The required quadratic polynomial
= x2 - 3x + (- 2)
= x2 - 3x - 2
Q 22. Write the number of zeroes of the polynomial y = f (x) whose graph is given in the figure.
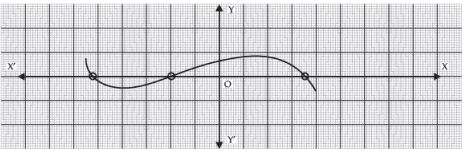
Since, curve (graph) of y = f (x) intersects the x-axis at three points,
∴ y = f (x) has three zeroes.
Q 23. The graph of y = f (x) is given in figure. How many zeroes are there of f (x)?
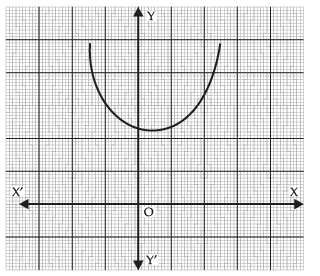
The graph of y = f (x) does not intersect the x-axis.
∴ The number of zeroes of f (x) is 0.
Q 24. The graph of y = f (x) is given in the figure. What is the number of zeroes of f (x)?
Since, the graph of y = f (x) intersects the x-axis at three distinct points,
∴ y = f (x) has 3 zeroes.
Q 25. What is the number of zeroes of the polynomial y = p (x)?
Since, the graph passes through origin(0,0) which means on putting x = 0, we get y = 0.
Therefore, (0,0) is the only root of this equation.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 2 Question Answers - Polynomials
| 1. What is a polynomial? |  |
| 2. How do you determine the degree of a polynomial? |  |
| 3. What is the difference between a monomial and a polynomial? |  |
| 4. How do you add or subtract polynomials? |  |
| 5. How do you multiply polynomials? |  |

|
Explore Courses for Class 10 exam
|

|


















