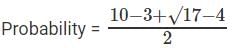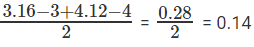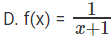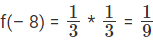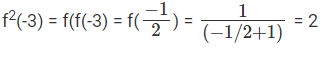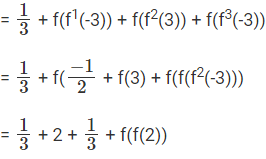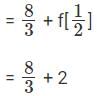Algebra: Functions Questions - 1 | Quantitative Aptitude (Quant) - CAT PDF Download
Question 1: How many onto functions can be defined from the set A = {1, 2, 3, 4} to {a, b, c}?
A. 81
B. 79
C. 36
D. 45
Ans: 36
Explanation:
First let us think of the number of potential functions possible. Each element in A has three options in the co-domain. So, the number of possible functions = 34 = 81.
Now, within these, let us think about functions that are not onto. These can be under two scenarios.
Scenario 1: Elements in A being mapped on to exactly two of the elements in B (There will be one element in the co-domain without a pre-image).
Let us assume that elements are mapped into A and B. Number of ways in which this can be done = 24 – 2 = 14
24 because the number of options for each element is 2. Each can be mapped on to either A or B
-2 because these 24 selections would include the possibility that all elements are mapped on to A or all elements being mapped on to B. These two need to be deducted.
The elements could be mapped on B & C only or C & A only. So, total number of possible outcomes = 14 * 3 = 42.
Scenario 2: Elements in A being mapped to exactly one of the elements in B. (Two elements in B without pre-image). There are three possible functions under this scenario. All elements mapped to a, or all elements mapped to b or all elements mapped to c.
Total number of onto functions = Total number of functions – Number of functions where one element from the co-doamin remains without a pre-image - Number of functions where 2 elements from the co-doamin remain without a pre-image.
⇒ Total number of onto functions = 81 – 42 – 3 = 81 – 45 = 36Choice C is the correct answer.
Question 2: Find the maximum value of f(x); if f(x) is defined as the Min {-(x – 1)2 + 2, (x – 2)2 + 1}
A. 1
B. 2
C. 0
D. 3
Ans: 2
Explanation:
First let us find the range where Min (-(x – 1)2 + 2, (x – 2)2 + 1) is – (x – 1)2 + 2.
In other words, in which range is – (x – 1)2 + 2 < (x – 2)2 + 1.
–(x2 – 2x +1) + 2 < x2 – 4x + 4 + 1
0 < 2x2 – 6x + 4
x2 – 3x + 2 > 0
(x – 1) (x – 2) > 0
⇒ x > 2 or x < 1
So, for x ∈ (1, 2) , f(x) = (x – 2)2 + 1
And f(x) = –(x – 1)2 + 2 elsewhere.
Let us also compute f(1) and f(2)
f(1) = 2, f(2) = 1
For x ∈ (-∞, 1), f(x) = –(x – 1)2 + 2
f(1) = 2
For x ∈ (1, 2), f(x) = (x – 2)2 + 1
f(2) = 1
For x ∈ (2, ∞), f(x) = –(x – 1)2 + 2
For x < 1 and x > 2, f(x) is -(square) + 2 and so is less than 2.
When x lies between 1 and 2, the maximum value it can take is 2. f(1) = 2 is the highest value f(x) can take.
As a simple rule of thumb, the best way to approach this question is to solve the two expressions. This gives us the meeting points of the two curves. One of the two meeting points should be the maximum value.Choice B is the correct answer.
Question 3: Consider functions f(x) = x2 + 2x, g(x) = √(x + 1) and h(x) = g(f(x)). What are the domain and range of h(x)?
Ans: Domain: (-∞, +∞), Range -[0, ∞]
Explanation:
h(x) = g(f(x)) = g(x2 + 2x) = √(x2 + 2x + 1) = √(x + 1)2 = |x + 1|
Domain of |x + 1| = (-∞, +∞), x can take any value.
As far as the range is concerned, |x + 1| cannot be negative. So, range = [0, ∞)
Question 4: [x] = greatest integer less than or equal to x. If x lies between 3 and 5, 5 inclusive, what is the probability that [x2] = [x]2?
A. Roughly 0.64
B. Roughly 0.5
C. Roughly 0.14
D. Roughly 0.36
Ans: Roughly 0.14
Explanation:
Let us take a few examples.
[32] = [3]2
[3.52] = 12 [3.5]2 = 9
[42] = 16 [4]2 = 16
For x ∈ (3, 5). [x]2 can only take value 9, 16 and 25.
Let us see when [x2] will be 9, 16 or 25.
If [x2] = 9,
x2 ∈ [9, 10)
⇒ x ∈ [3, √10)
[x2] = 16
x2 ∈ [16, 17)
⇒ x ∈ [4, √17)
In the given range [x2] = 25 only when x = 5
So [x2] = [x]2 when x ∈ [3, √10] or [4, √10) or 5.
Choice C is the correct answer.
Question 5: Give the domain and range of the following functions:
A. f(x) = x2 + 1
B. g(x) = log(x + 1)
C. h(x) = 2x
D. f(x) = 1/(x+1)
E. p(x) = |x + 1|
F. q(x) = [2x], where [x] gives the greatest integer less than or equal to x
Explanation:
A. f(x) = x2 + 1
Domain = All real numbers (x can take any value)
Range [1, ∞). Minimum value of x2 is 0.
B. g(x) = log (x + 1)
Domain = Log of a negative number is not defined so (x + 1) > 0 or x > -1
Domain (-1, ∞)
Range = (-∞, +∞)
Note: Log is one of those beautiful functions that is defined from a restricted domain to all real numbers. Log 0 is also not defined. Log is defined only for positive numbers
C. h(x) = 2x Domain - All real numbers.
Range = (0, ∞)
The exponent function is the mirror image of the log function.
Domain = All real numbers except -1
Range = All real numbers except 0.
E. p(x) = |x + 1|
Domain = All real numbers
Range = [0, ∞) Modulus cannot be negative
F. q(x) = [2x], where [x] gives the greatest integer less than or equal to x
Domain = All real numbers
Range = All integers
The range is NOT the set of even numbers. [2x] can be odd. [2 * 0.6] = 1. It is very important to think fractions when you are substituting values.
Question 6: How many elements are present in the domain of 9–xCx+1?
A. 5
B. 6
C. 4
D. 7
Ans: 6
Explanation:
For nCr to be defined, we should have r greater than or equal to zero and, n greater than or equal to r.
Therefore 9 – x ≥ x + 1 or 4 ≥ x and
also x + 1 > 0 or x > –1
Therefore x takes on the values {–1,0,1,2,3,4}
Therefore domain = {–1,0,1,2,3,4} and range = {10C0,9C1,8C2,7C3,6C4,5C5}
There are 6 elements in the domain.Choice B is the correct answer.
Question 7: f(x + y) = f(x)f(y) for all x, y, f(4) = + 3 what is f(–8)?
A. 1/3
B. 1/9
C. 9
D. 6
Ans: 1/9
Explanation:
f(x + 0) = f(x) f(0)
f(0) = 1
f(4 + – 4) = f(0)
f(4 + – 4) = f(4) f(–4)
1 = +3 * f(–4)f(-4) = 1/3
f(– 8) = f(– 4 + (– 4)) = f(– 4) f(– 4)
Choice B is the correct answer.
Question 8: If f(x – 3) = 2x3 + p – qx and f(x2 – 4) = x2 – 8q + 6p, then what is the value of p – q?
A. 5
B. 10
C. 6
D. Cannot determine
Answer: 10
Explanation:
f(x – 3) = 2x3 + p – qx
Let x = 3, then f(0) = 54 + p – 3q ---- (1)
f(x2 – 4) = x2 – 8q + 6p
Let x2 = 4, then f(0) = 4 – 8q + 6p --- (2)
From (1) and (2)
54 + p – 3q = 4 – 8q + 6p
50 = 5p – 5q
p - q = 10Choice B is the correct answer.
Question 9: Given that x is real and f(x) = f(x + 1) + f(x – 1). Determine the value of ‘a’ that will satisfy f(x) + f(x + a) = 0
A. -1
B. -2
C. 1
D. 3
Ans: 3
Explanation:
f(x) = f(x + 1) + f(x – 1)
Let f(x) = p and f(x – 1) = q
f(x + 1) = f(x + 1 + 1) + f(x + 1 – 1) (Put x = x + 1 here!)
= f(x + 2) + f(x)
p – q = f(x + 2) + p
Or f(x + 2) = -q
f(x + 2) = f(x + 2 + 1) + f(x + 2 – 1) (Put x = x + 2 here!)
= f(x + 3) + f(x + 1)
– q = f(x + 3) + p – q
Or f(x + 3) = -p
At this point we notice that f(x) = p and f(x+3) = -p
f(x) + f(x + 3) = 0 (This is the condition to be satisfied to determine a)
Hence ‘a’ = 3Choice D is the correct answer.
Question 10: x is a real number such that f(x) = 1/x when x > 0 and f(x) = 1/x+1 otherwise. Also fn(x) = f(fn - 1 (x)). What is f(3) + f2(-3) + f3(3) + f4(-3)?
A. -2/3
B. 14/3
C. 0
D. 3
Ans: 14/3
Explanation:
f(x) = 1/x = when x > 0; f(x) = 1/x+1 otherwise
f(3) = 1/3
f2(3) = f(f(3) = f (1/3) = 3
f(3) + f2(-3) + f3(3) + f4(-3)
= 14/3
Choice B is the correct answer.
Question 11: Which of the following functions are identical?
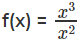
g(x) = (√x)2
h(x) = x
A. f(x) and g(x)
B. f(x) and h(x)
C. All 3 are identical
D. None of these
Ans: None of these
Explanation:
For functions to be identical, their domains should be equal
f(x) – x can’t be zero
g(x) – x can’t be negative
h(x) – x can take all possible valuesChoice D is the correct answer.
|
191 videos|133 docs|109 tests
|
FAQs on Algebra: Functions Questions - 1 - Quantitative Aptitude (Quant) - CAT
| 1. What is a function in algebra? |  |
| 2. How do you determine if a relation is a function? |  |
| 3. How do you find the domain and range of a function? |  |
| 4. What is the difference between a linear function and a quadratic function? |  |
| 5. How do you solve equations involving functions? |  |