Algebraic Methods of Solving Pair of Linear Equations in Two Variables | Mathematics (Maths) Class 10 PDF Download
Akhila's Fair Adventure
Let’s imagine a situation, Ankita went to a fair in her village. She wanted to go on rides like the Giant Wheel and play Hoopla (a game in which a ring is thrown on the items kept in a stall, and if the ring covers any object completely, the player gets it). The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. If each ride on the giant wheel costs Rs 3, and a game of Hoopla costs Rs 4, find out the number of rides she had and how many times she played Hoopla, provided she spent Rs 20.
Setting Up the Equations
For solving such kind of problem, the first step is to formulate it in terms of equations. Let x be the number of times Ankita rode on the Giant Wheel and y be the number of times she played Hoopla. The equations become,
x = 2y,
3x + 4y = 20.
Can we find the solution to this system of equations? There are several ways of finding solutions, let’s look at them in detail.
Pair of Linear Equations in Two Variables
An equation that can be put in the form of ax + by + c = 0, where a, b, and c are real numbers and a and b are both non-zero is called a linear equation in two variables x and y. Geometrically, if all the points satisfying this equation are plotted on the cartesian plane. It represents a line.
Similarly, a system of two linear equations represents two lines. The solution to that system represents points that satisfy both of the equations. There can be either no point, one point, and infinitely many points.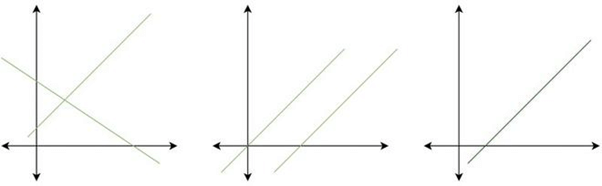 One Solution, No Solution, and Infinitely many solutions.
One Solution, No Solution, and Infinitely many solutions.
Algebraic Methods of Solving a Pair of Linear Equations
There are several methods of solving a system of linear equations algebraically, let’s look at two of those methods:
- Substitution Method
- Elimination Method
1. Substitution Method
This method mainly involves two steps:
Step 1: Find the value of one variable, say y in terms of the other variable, i.e., x from either equation, whichever is convenient.
Step 2: Substitute this value of y in the other equation, and reduce it to an equation in one variable, i.e., in terms of x, which can be solved.
Q.1. Solve the following system of equations:
7x – 15y = 2
x + 2y = 3
Solution: It can be solved according to the steps explained above,
We pick an equation to represent value of one variable in terms of others,
Let’s pick, x = 3 - 2y (It’s also convenient).
Substitute the value of x in the other equation.
7(3 - 2y) -15y = 2
⇒ 21 - 14y - 15y = 2
⇒ 19 = 29y
⇒ y = 19 / 29
Now, the x value becomes x = 3 – 2(19 / 29) = 3 – (38 / 29) = 49 / 29
This solution can also be checked by substituting both the values in these equations.
Note: We have substituted the value of one variable by expressing it in terms of other variable to solve the problem. That’s why this method is called substitution.
Sometimes, as in the Example below, we can get statements with no variable. If this statement is true, we can say that the pair of linear equations has infinitely many solutions. If the statement is false, then the pair of linear equations is inconsistent.
Q.2. Anuj and Rahul bought some stationery items from the shop. Anuj bought 2 pencils and 3 erasers. The cost of 2 pencils and 3 erasers was Rs 9 and Rahul bought 4 pencils and 6 erasers. The cost of 4 pencils and 6 erasers is Rs 18. Find the cost of each pencil and each eraser.
Solution: The pair of linear equations that is formed from the above description is,
2x + 3y = 9
4x + 6y = 18
where x is the cost of a pencil and y is the cost of eraser.
X = (9 - 3y) / 2
Putting this value in the other equation.
4(9 - 3y / 2) + 6y = 18
18 - 6y + 6y = 18
18 = 18
This statement is true for all values of y. However, we do not get a specific value of y as a solution. Therefore, we cannot obtain a specific value of x. This situation has arisen because both the given equations are the same. Therefore, these equations both have infinitely many solutions.
2. Elimination Method
This method mainly involves the following steps:
- Multiply both the equations by some suitable non-zero constants and make the coefficients of one variable (either x or y) numerically equal.
- Add or subtract one equation from the other so that one variable gets eliminated.
- If an equation in one variable is obtained, go to Step 5. If in Step 2, we obtain a true statement involving no variable, then the original pair of equations has infinitely many solutions.
- If in Step 2, we obtain a false statement involving no variable, then the original pair of equations has no solution, i.e., it is inconsistent.
- Solve the equation in one variable (x or y) so obtained to get its value.
- Substitute this value of x (or y) in either of the original equations to get the value of the other variable.
Q.1. Find all possible solutions of the following system of equations using the elimination method.
2x + 3y = 8 – (1)
4x + 6y = 7 – (2)
Solution: Multiply equation (1) by 2 and equation (2) by 1. This will make coeffecients of x in both the equations same. Then we get the equations as:
4x + 6y = 16
4x + 6y = 7
Subtracting both of the equations,
we get 0 = 9
This is false. So, no solution exists for this system of linear equations.
Q.2. The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?
Solution: Let x and y be the ten’s and unit’s digit respectively. So the first number can be written as 10x + y is the expanded form(for example 56 = 10(6) + 5).
(10x + y) + (10y + x) = 66,
i.e ⇒ 11(x + y) = 66 i.e ⇒ x + y = 6
It’s also given that the digits differ by 2,
So, either x – y = 2 or y – x = 2.
Let’s look for both of the cases,
Case 1: x – y = 2,
Substituting x = y + 2 in the equation given above,
y + 2 + y = 6
⇒ 2y = 4
⇒ y = 2.
So, x = 4
Case 2: y – x = 2,
Substituting y = x + 2, in the equation given above,
x + y = 6.
⇒ x + x + 2 = 6
⇒ 2x = 4
⇒ x = 2
y = 4.
Cross-Multiplication Method
It is one of the techniques to determine the solution of a linear equation in two variables, it is known to be the quickest method.
Assume a pair of Linear equation:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
By using Cross-multiplication, we can find the values of ‘x’ and ‘y’:
x = (b1c2) - (b2c1) / (b2a1) - (b1a2)
y = (c1a2) - (c2a1) / (b2a1) - (b1a1)
Derivation for Cross-multiplication
a1x + b1y + c1 = 0 ⇢(1)
a2x + b2y + c2 = 0 ⇢(2)
Multiply with b2 in equation (1) and b1 in equation (2):
a1b2x + b1b2y + c1b2 = 0 ⇢(3)
a2b1x + b1b2y + c2b1 = 0 ⇢(4)
Subtracting equation (4) from equation (3) will provide the values of x and y as,
x = (b1c2) - (b2c1) / (b2a1) - (b1a2)
y = (c1a2) - (c2a1) / (b2a1) - (b1a1)
Easy Technique to understand the formulae
Write down coefficients in Original form:
a1 b1 c1
a2 b2 c2
Ignore the Coefficients of x and cross- multiply the remaining coefficients then subtract them: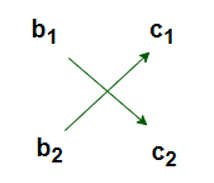 Thus, the solution of the equation of part one becomes ⇒
Thus, the solution of the equation of part one becomes ⇒ 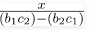
Now, Ignore the coefficient of y and cross-multiply the remaining terms: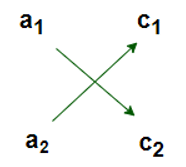
Remember to consider the equation under (-y), The second part of the solution ⇒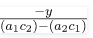
For the third part, ignore the coefficients of 1 and cross-multiply the remaining terms and subtract them: The third part of the equation becomes ⇒
The third part of the equation becomes ⇒ 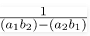
Combining all the three parts ⇒ 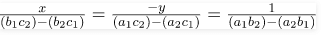
Q.1. Find the value of the variables satisfying the equation using cross- multiplication method:
2x + 3y = 11
3x + 2y = 9
Solution: Write equations in general form:
2x + 3y – 11 = 0
3x + 2y – 9 = 0
Using Cross- multiplication method,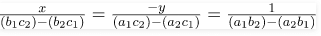
Put the values of all the coefficients in the formula,

x / -5 = -y / 15 = 1 / -5
Solving, we get: x = 1, y = 3
Q.2. Using Cross-multiplication method, solve for x and y:
3x – 4y – 2 = 0
y – 2x – 7 = 0
Solution: Using the formula: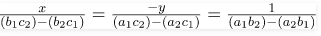
Substitute the values in the formula:
Solving the equation, x = -6, y = -5
|
127 videos|584 docs|79 tests
|
FAQs on Algebraic Methods of Solving Pair of Linear Equations in Two Variables - Mathematics (Maths) Class 10
| 1. What are the different methods to solve a pair of linear equations in two variables? |  |
| 2. How do you use the substitution method to solve a pair of linear equations? |  |
| 3. What is the elimination method and how is it applied? |  |
| 4. Can a pair of linear equations have no solution? |  |
| 5. How can you check the solution of a pair of linear equations? |  |





















