Approximations and Exponential Series | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Approximations |

|
| Exponential series |

|
| Logarithmic series |

|
| Comparison Between Exponential and Logarithmic Series |

|
Approximations
If x < 1, the terms of the above expansion go on decreasing and if x be very small, a stage may be reached when we may neglect the terms containing higher powers of x in the expansion. Thus, if x be so small that its squares and higher powers may be neglected then (1 + x)n = 1 + nx, approximately,
This is an approximate value of (1 + x)n
Example1: If x is so small such that its square and higher powers may be neglected then find the approximate value of
Sol:
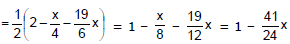
Example 2: The value of cube root of 1001 upto five decimal places is
Sol:
(1001)1/3 = (1000 + 1)1/3 =
= 10 {1 + 0.0003333 -0.00000011 + ......} = 10.00333
Example 3: The sum of is
Sol: Comparing with
1 + nx + + ...... ⇒ nx = 1/4 ...(i)
& or
⇒ ⇒
⇒ ...(ii) {by (i)}
putting the value of x in (i) ⇒ ⇒ n =
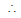 sum of series = (1 + x)n = (1 -1/2)-1/2 = (1/2)-1/2 =
sum of series = (1 + x)n = (1 -1/2)-1/2 = (1/2)-1/2 =
Exponential series
(a) e is an irrational number lying between 2.7 & 2.8. Its value correct upto 10 places of decimal is 2.7182818284.
(b) Logarithms to the base 'e' are known as the Napierian system, so named after Napier, their inventor. They are also called Natural Logarithm.
(c) where x may be any real or complex number &
(d)
(e)
Example 4: Approximate e0.1 up to 3 decimal places using series.
Sol: 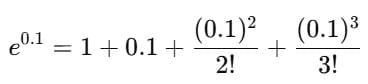
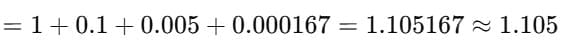
Logarithmic series
(a) ln (1 + x) = x - where
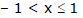
(b) ln (1 -x) = where
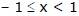
Remember :
(i)
(ii) eln x = x
(iii) ln2 = 0.693
(iv) ln 10 = 2.303
Example 5: Expand ln(1.1) using logarithmic series.
Sol: 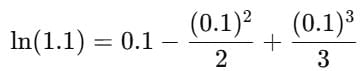
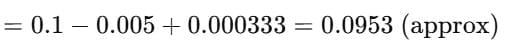
Example 6: Prove that 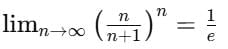
Sol: Taking log: 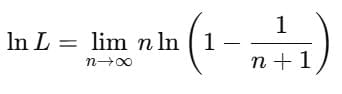
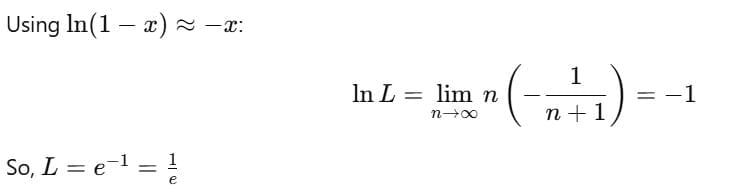
Comparison Between Exponential and Logarithmic Series

|
172 videos|503 docs|154 tests
|
FAQs on Approximations and Exponential Series - Mathematics (Maths) for JEE Main & Advanced
| 1. What are approximations and why are they important in mathematics? |  |
| 2. How are exponential series used in mathematics and real-life applications? |  |
| 3. Can approximations be used to solve equations or find roots of functions? |  |
| 4. What is the difference between linear and exponential approximations? |  |
| 5. Are there any limitations or drawbacks to using approximations in mathematics? |  |















