Area of a Triangle and Equation of a Plane | Mathematics (Maths) Class 12 - JEE PDF Download
D. AREA OF A TRIANGLE
Show that the area of a triangle whose vertices are the origin and the points 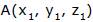 and
and 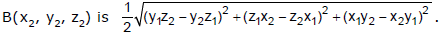
The direction ratios of OA are 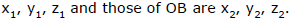
Also OA 
and OB 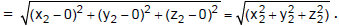
∴ the d.c.’ s of OA are 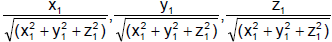
and the d.c.’s of OB are 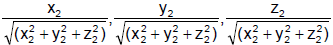
Hence if θ is the angle between the line OA and OB, then
sin θ 
Hence the area of ΔOAB
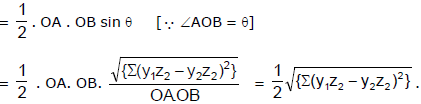
Ex.6 Find the area of the triangle whose vertices are A(1, 2, 3), B(2, –1, 1)and C(1, 2, –4).
Sol. Let Δx, Δy, Δz be the areas of the projections of the area Δ of triangle ABC on the yz, zx and xy-planes respectively. We have
Δx =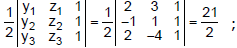
Δy =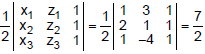
Δz =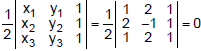
∴ the required area Δ = 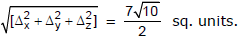
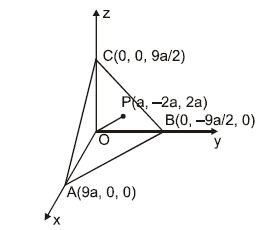
Ex.7 A plane is passing through a point P(a, –2a, 2a), 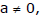 at right angle to OP, where O is the origin to meet the axes in A, B and C. Find the area of the triangle ABC.
at right angle to OP, where O is the origin to meet the axes in A, B and C. Find the area of the triangle ABC.
Sol. OP 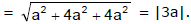
Equation of plane passing through P(a, –2a, 2a) is
A(x – a) + B(y + 2a) + C(z – 2a) = 0.
∵ the direction cosines of the normal OP to the plane ABC are proportional to a – 0, –2a – 0, 2a – 0 i.e. a, –2a, 2a. ⇒ equation of plane ABC is
a(x – a) – 2a(y + 2a) + 2a(z – 2a) = 0 or ax – 2ay + 2az = 9a2 ....(1)
Now projection of area of triangle ABC on ZX, XY and YZ planes are the triangles AOC, AOB and BOC respectively.
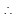
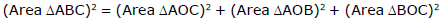
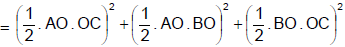
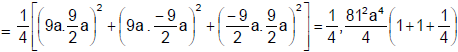
|
223 videos|377 docs|167 tests
|
FAQs on Area of a Triangle and Equation of a Plane - Mathematics (Maths) Class 12 - JEE
| 1. What is the formula for finding the area of a triangle? |  |
| 2. How do you calculate the area of a triangle if you know the lengths of its sides? |  |
| 3. Can you find the area of a triangle if you know only the lengths of two sides and the included angle? |  |
| 4. How can you determine the equation of a plane given three non-collinear points on the plane? |  |
| 5. Is it possible to find the equation of a plane if you know the coordinates of a point on the plane and the normal vector of the plane? |  |
















