Areas Related Circles Exercise 15.2 | Extra Documents, Videos & Tests for Class 10 PDF Download
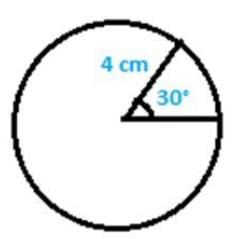
Q1. Find in terms of π, the length of the arc that subtends an angle of 30 degrees, at the center of ‘O’ of the circle with a radius of 4 cm.
Soln:
Given Data :
Radius = 4 cm
Angle subtended at the centre ‘O’ = 30°
Formula to be used :
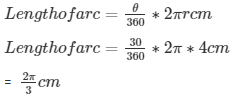
Therefore, the Length of arc the length of the arc that subtends an angle of 60 degrees is 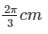
Q2. Find the angle subtended at the centre of circle of radius 5 cm by an arc of length 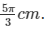
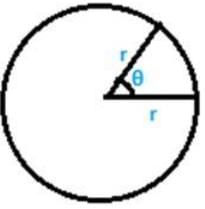
Soln:
Given data:
Radius = 5 cm
Length of arc 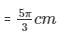
Formula to be used:
Length of arc 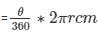
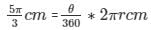
Solving the above equation, we have:
θ = 60°
Therefore, angle subtended at the centre of circle is 60°
Q3. An arc of length cm subtends an angle of 144° at the center of the circle.
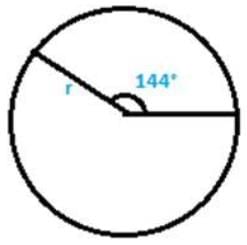
Soln:
Given Data : length of arc = cm
θ = angle subtended at the centre of circle = 144°
Formula to be used :
Length of arc 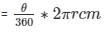
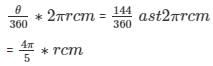
As given in the question, length of arc = cm ,
Therefore, 
Solving the above equation, we have
r = 25 cm.
Therefore the radius of the circle is found to be 25 cm.
Q4. An arc of length 25 cm subtends an angle of 55° at the center of a circle. Find in terms of radius of the circle.
Soln:
Given Data :
length of arc =25 cm
θ = angle subtended at the centre of circle = 55°
Formula to be used :
Length of arc 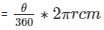
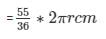
As given in the question length of arc =25 cm ,hence,
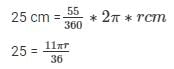
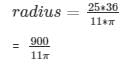
Therefore, the radius of the circle is 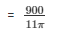
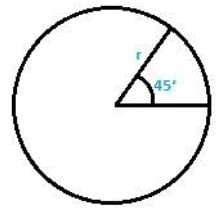
Q5. Find the angle subtended at the center of the circle of radius ‘a’ cm by an arc of 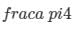 length cm .
length cm .
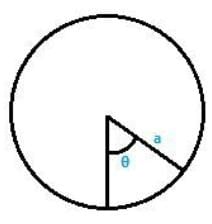
Soln:
Given data :
Radius = a cm
Length of arc = 
θ = angle subtended at the centre of circle
Formula to be used:
Length of arc 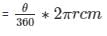
Length of arc 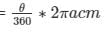
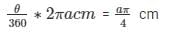
Solving the above equation, we have
θ = 45°
Therefore, the angle subtended at the centre of circle is 45°
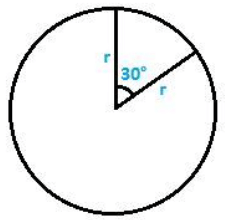
Q6. A sector of the circle of radius 4 cm subtends an angle of 30°. Find the area of the sector.
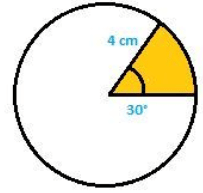
Soln:
Given Data:
Radius = 4 cm
Angle subtended at the centre ‘O’ = 30°
Formula to be used :
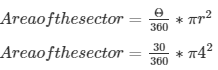
Solving the above equation, we have:
Area of the sector = 4.9 cm2
Therefore, Area of the sector is found to be 4.9 cm2
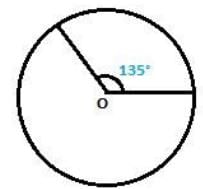
Q7. A sector of a circle of radius 8 cm subtends an angle of 135°. Find the area of sector.
Soln:
Given Data:
Radius = 8 cm
Angle subtended at the centre ‘O’ = 135°
Formula to be used:
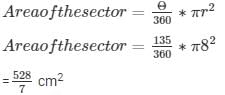
Therefore, Area of the sector calculated is 528/7 cm2
Q8. The area of sector of circle of radius 2 cm is cm2. Find the angle subtended by the sector.

Soln:
Given Data:
Radius = 2 cm
Angle subtended at the centre ‘O’ =?
Area of sector of circle = cm2
Formula to be used:

As given in the question area of sector of circle = cm2
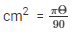
Solving the above equation, we have
θ = 90°
Therefore, the angle subtended at the centre of circle is 90°
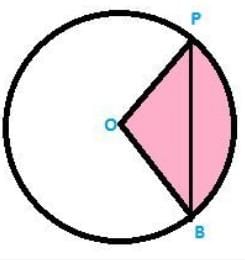
Q9. PQ is a chord of circle with centre ‘O’ and radius 4 cm. PQ is of the length 4 cm. Find the area of sector of the circle formed by chord PQ.
Soln:
Given Data: PQ is chord of length 4 cm.
Also, PO = QO= 4 cm
OPQ is an equilateral triangle.
Angle POQ = 60°
Area of sector ( formed by the chord (shaded region ) ) = ( area of sector )
Formula to be used:

Therefore, Area of the sector is 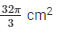
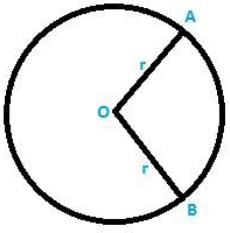
Q10. In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector.
Soln:
Given Data:
Radius = 35 cm
Angle subtended at the centre ‘O’ = 72°
Area of sector of circle =?
Formula to be used: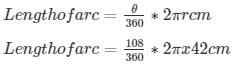
Solving the above equation we have,
Length of arc = 44 cm
We know that,
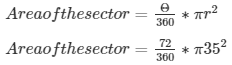
Solving the above equation, we have, Area of the sector = ( 35 x 22 ) cm2
Therefore, Area of the sector is 770 cm2
Q11. The perimeter of a sector of a circle of radius 5.7 m is 27.2m. find the area of the sector.
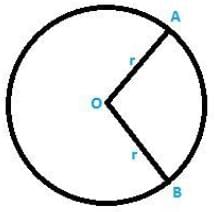
Soln:
Given Data:
Radius = 5.7 cm = OA = OB [from the figure shown above]
Perimeter = 27.2 m
Let the angle subtended at the centre be θ
Perimeter = 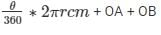
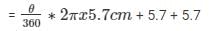
Solving the above equation we have,
θ = 158.8°
We know that,
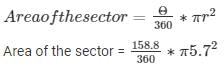
Solving the above equation we have,
Area of the sector = 45.048 cm2
Therefore, Area of the sector is 45.048 cm2
Q12. The perimeter of a certain sector of a circle of radius is 5.6 m and 27.2 m. find the area of a sector.
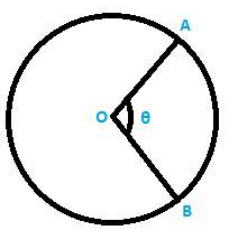
Soln:
Given data:
Radius of the circle = 5.6 m = OA = OB
(AB arc length) + OA + OB = 27.2
Let the angle subtended at the centre be θ
We know that,
Length of arc =
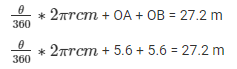
Solving the above equation, we have,
θ = 163.64°
We know that,
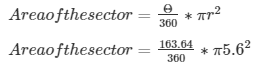
On solving the above equation, we have,
Area of the sector = 44.8 cm2
Therefore, Area of the sector is 44.8 cm2
Q13. A sector was cut from a circle of radius 21 cm. The angle of sector is 120°. Find the length of its arc and its area.
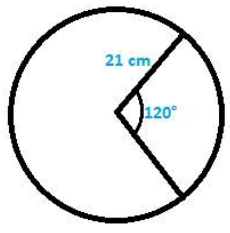
Soln:
Given data:
Radius of circle ( r ) = 21 cm
θ = angle subtended at the centre of circle = 120°
Formula to be used:
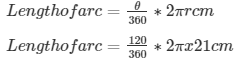
On solving the above equation, we get,
Length of arc = 44 cm
We know that,
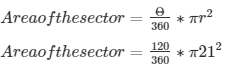
Area of the sector = ( 22 x 21 ) cm2
Therefore, Area of the sector is 462 cm2
Q14. The minute hand of a circle is 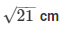 long. Find the area described by the minute hand on the face of clock between 7:00 a.m to 7:05 a.m.
long. Find the area described by the minute hand on the face of clock between 7:00 a.m to 7:05 a.m.
Soln:
Given data:
Radius of the minute hand (r)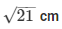
Time between 7:00 a.m to 7:05a.m = 5 min
We know that, 1 hr = 60 min, minute hand completes
One revolution = 360°
60 min = 360°
θ = angle subtended at the centre of circle = 5 x 6° = 30°

Area of the sector = 5.5 cm2
Therefore, Area of the sector is 5.5 cm2
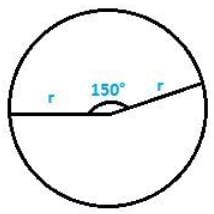
Q 15. The minute hand of clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 8 a.m to 8:25 a.m.
Soln:
Given data:
Radius of the circle = radius of the clock = length of the minute hand = 10 cm
We know that, 1 hr = 60 min
60 min = 360°
1 min = 6°
Time between 8:00 a.m to 8:25 a.m = 25 min
Therefore, the subtended = 6° x 25 = 150°
Formula to be used :
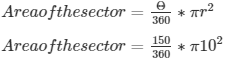
Area of the sector = 916.6 cm2= 917 cm2
Therefore, Area of the sector is 917 cm2
Q16. A sector of 56° cut out from a circle subtends area of 4.4 cm2. Find the radius of the circle.
Soln:
Given data:
Angle subtended by the sector at the centre of the circle, θ = 56°
Let the radius of the circle be = ‘r’ cm
Formula to be used:

On solving the above equation, we get,
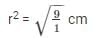
r = 3 cm
Therefore, radius of the circle is r = 3 cm
Q17. In circle of radius 6 cm. Chord of length 10 cm makes an angle of 110° at the centre of circle. Find:
(i) Circumference of the circle
(ii) Area of the circle
(iii) Length of arc
(iv) The area of sector
Soln:
Given data:
Radius of the circle = 6 cm
Chord of length = 10 cm
Angle subtended by chord with the centre of the circle = 110°
Formulae to be used:
Circumference of a circle = 2
Area of a Circle =
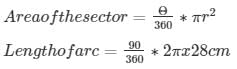
Circumference of a circle = 2 = 2 x 3.14 x 8 = 37.7 cm
Area of a Circle = = 3.14 x 6 x 6 = 113.14 cm2
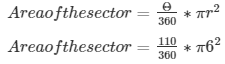
On solving the above equation we get,
Area of the sector = 33.1 cm2
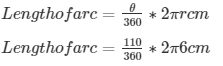
On solving the above equation we get,
Length of arc = 22.34 cm.
Therefore,Circumference = 37.7 cm
Area of a Circle = 113.14 cm2
Area of the sector = 33.1 cm2
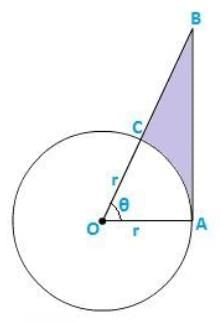
Q18. The given figure shows a sector of a circle with centre ‘O’ subtending an angle θ°. Prove that:
1. Perimeter of shaded region is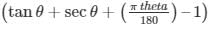
2. Area of the shaded region is 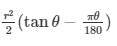
Soln:
Given Data: Angle subtended at the centre of the circle = θ°
Angle OAB = 90° [ at point of contact, tangent is perpendicular to radius ]
OAB is a right angle triangle

Perimeter of the shaded region = AB + BC + CA ( arc )

Area of the shaded region = ( area of triangle AOB ) – ( area of sector )

On solving the above equation we get,

Q 19. The diagram shows a sector of circle of radius ‘r’ cm subtends an angle θ. The area of sector is A cm2and perimeter of sector is 50 cm. Prove that 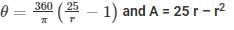
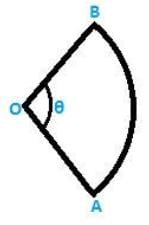
Soln:
Given Data:
Radius of circle = ‘r’ cm
Angle subtended at centre of the circle = θ
Perimeter = OA + OB + (AB arc)
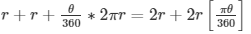
As given in the question, perimeter = 50
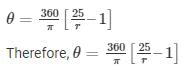
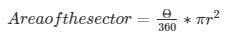
On solving the above equation, we have
A = 25r – r2
Hence, proved.
|
5 videos|292 docs|59 tests
|
FAQs on Areas Related Circles Exercise 15.2 - Extra Documents, Videos & Tests for Class 10
| 1. What is the formula for finding the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. Can you find the area of a circle if only the circumference is given? |  |
| 4. What is the relationship between the radius and diameter of a circle? |  |
| 5. How can the area of a sector of a circle be calculated? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















