Areas of Trapezium, Polygons & General Quadrilaterals | Mathematics (Maths) Class 8 PDF Download
Trapezium
Mensuration is the branch of mathematics that deals with the study of Geometric shapes, their area, volume, and other related parameters. A four-sided closed figure in which one pair of parallel sides opposite to each other and another non-pair of non-parallel sides is called a trapezium.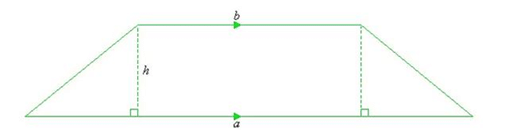
Properties of Trapezium
- It is a Four-sided Closed Figure with a sum of interior angles 360°.
- One pair of Parallel sides which should be opposite to each other.
- One pair of non-parallel sides.
- Sum of the angles of adjacent sides is 180°.
- Diagonals of a trapezium bisect each other on intersection.
Basic Terminology for Trapezium
- Base of a Trapezium: The pair of parallel sides which are opposite to each other are called base. You can call as b1 and b2 respectively.
- Height of a Trapezium: The perpendicular distance between the two parallel lines is called as Height of the trapezium.
Formula for Area of Trapezium
If the base and height of a trapezium are given, then the area of a Trapezium can be calculated with the help of the formula: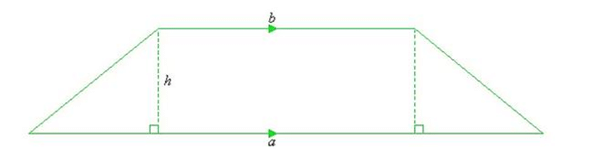
Area of Trapezium = 1/2 x (sum of bases) x (Height of trapezium)
Derivation for Area of a Trapezium
The area of a trapezium is equal to the sum of the areas of the two triangles and the area of the rectangle. Following is the derivation for calculating the area of the trapezium:
Since we know that:
Area of trapezium = Area of triangle 1 + area of rectangle + Area of triangle 2
Let us suppose the base of triangle 1 be B1 and base of triangle 2 is B2 and the height be h for both the triangles. And for rectangle assume its breadth and height be b1 and h.
That means,
A = (B1 x h / 2) + b1h + (B2 x h / 2)
A = (B1 x h + 2b1h + B2 x h) / 2
Simplifying the equation, and rearranging the terms, and factoring result to:
A = h / 2[b1 + (B1 + b1 + B2] ….(i)
If we assume the longer base of the trapezoid be b2, then
b2 = B1 + b1 + B2 …..(ii)
Substituting (ii) in equation (i),
A = h / 2(b1 + b2)
Therefore, the area of a trapezoid with bases b1, b2, and altitude h is;
A = h/2(b1+b2)
which can also be written as below-
Area of Trapezium = 1 / 2 x (sum of bases) x (Height of trapezium)
= 1 / 2 x ( b1 + b2) x h
Sample Problems based on the Formula
Problem 1: Calculate the area of the trapezium in which the value of bases are 10 and 5 respectively and the height of trapezium is 2 m.
Solution:
Since we know that,
Area of trapezium = 1/2 x (sum of bases) x (Height of trapezium)
= 1/2 x (10 + 5) x 2
= 15 m^2
Problem 2: Given the area of trapezium as 120 m^2 and height of trapezium is 6m and one of base is 4m. Calculate the length of the other base.
Solution:
Area of trapezium = 1/2 x(sum of bases) x ( Height of trapezium)
Let value of other base is b2
Putting all the given values in the above formula, we got
120 = 1/2 x (4 + b2) x 6
120 = (4 + b2) x3
40 = (4 + b2)
b2 = 36 meter
Problem 3: Given the area of trapezium as 220 m^2 and one base is 6m and another base is 4m. Calculate the height of the trapezium.
Solution:
Area of trapezium = 1/2 x (sum of bases) x ( Height of trapezium)
Let value of height be h.
Putting all the given values in the above formula, we got
220 = 1/2 x (4 + 6) x h
220 = 10 x h
22 = h
h = 22m
Area of irregular Polygons
Area of Polygons
Mensuration is the branch of mathematics that deals with the study of different geometrical shapes and their areas. It uses geometric calculations and algebraic equations to compute the measurement of various aspects of objects. In geometry, a polygon can be defined as a flat or plane, two-dimensional closed shape with straight sides. It does not have curved sides.
Can you think of a two-dimensional shape closed with straight lines? How it looks and how can you define this shape? We call this shape a polygon. To form a polygon we need a minimum of three line segments because polygon is a closed shape. So the smallest polygon is a triangle because it has three sides.
If a polygon has 4 sides or line segments then it’s known as a Quadrilateral. If a polygon has 5 sides or line segment then it’s known as Pentagon. If a polygon has 6 sides or line segments then it’s known as Hexagon. If a polygon has 7 sides or line segments then it’s known as Heptagon and so on.
Parts of Polygons
Face of Polygon
A face refers to the flat surface of a polygon. Name of the Polygon can be suggested by its face.
Edges of Polygon
An edge is a line segment on the boundary joining one vertex (corner point) to another. They serve as the junction of two faces. The faces meet at edges which are lines.
Sides- Line segments that are used to form a polygon, it’s denoted by n.
Interior Angles- Interior angles are formed between the adjacent sides inside the polygon and are equal to each other. The number of interior angles is equal to the number of sides mean. For example, a triangle has 3 interior angles, a Quadrilateral has 4 interior angles, Pentagon has 5 interior angles and a hexagon has 6 interior angles.
Interior angle = 180° – exterior angle
Exterior Angles- Exterior is formed by extending one side of the polygon and the angle between that extension and the adjacent side is known as the exterior angle.
Exteior angle of any polygon 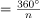 n is number of sides.
n is number of sides.
Vertices of Polygon
A point where two or more lines meet is called a vertex. It is a corner. The point of intersection of edges denotes the vertices. These edges meet at vertices which are points.
Polygon is formed by joining lines also we name the polygon according to the number of sides if a polygon has three sides then it’s known as Triangle if the number of sides is 4 then it is known as a Quadrilateral.
For example Triangle, Quadrilateral, Pentagon, Hexagon, Heptagon, Octagon, Nonagon, Decagon, and so on.
Concave or Convex Polygon
A convex polygon has no angles pointing inwards. The mean value of the internal angle of all internal angles is always less than 180°.
If any internal angle is greater than 180° then the polygon is known as concave.
There are two types of polygons in geometry:
1. Regular Polygon
2. Irregular Polygon
Regular Polygon
Now think about the polygon having equal sides and equal angles. How can you define this polygon and how you will get the area of the polygon. As the sides and angles of this polygon are equal, so we can define this polygon as a regular polygon. A regular n-sided polygon has rotational symmetry of order n.
All vertices of a regular polygon lie on a common circle know as the circumscribed circle because they are noncyclic points. A regular polygon is a cyclic polygon.
 Regular Triangle- Equilateral Triangle
Regular Triangle- Equilateral Triangle
 Quadrilateral – Square
Quadrilateral – Square
 Pentagon – Regular Pentagon
Pentagon – Regular Pentagon
 Hexagon -Regular Hexagon
Hexagon -Regular Hexagon
Question: What is the exterior and interior angle of a regular hexagon?
Answer: As we know regular hexagon is formed by joining 6 line segments so number of sides in hexagon is 6.
Exterior Angle = 360o/n = 360o/6 = 60o
Interior angle = 180° – exterior angle = 180° – 60° = 120°
A polygon having equal sides and equal angles is a regular polygon.
Area of regular polygon =(½) x Perimeter x Apothem
Example: Find the area of the regular polygon if the perimeter of the polygon is 20 cm and Apothem is 5 cm.
Solution:
Area of regular polygon =(½) x 20 cm x 5 cm = 50 cm2
Irregular Polygon
Think about a polygon having different angles and different sides. You cannot find out the area of this polygon as a regular polygon. Such type of polygons are defined as irregular polygons.
Vertices– A point where two or more lines meet is called a vertex. The point of intersection of edges denotes the vertices.
Sides- Lines segment which is used to form a polygon, it’s denoted by n. Here in irregular polygon length of each side is not equal.
Exterior angle- The sum of the exterior angles of an irregular polygon also equals 360° but the angles are not equivalent. Because irregular polygons have interior angles with different measurements, because of that each exterior angle has a different measurement as well.
Area of Irregular Polygon
To find the area of an irregular polygon you first separate the shape into regular. Then use the regular polygon area formulas to find the area of each of those polygons. Later add the area of all regular polygons to get the area of an irregular polygon.
To find the area of a triangle, we use the following formula:
Area of triangle=(1/2) x Base x Height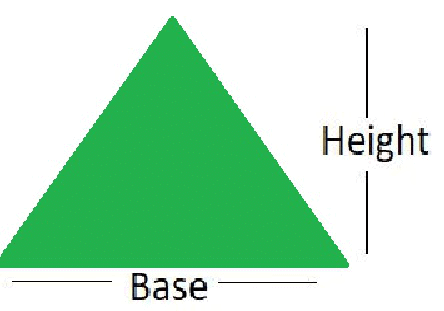
To find the area of a quadrilateral, we can divide the quadrilateral into two triangles by constructing a diagonal and find the area of the triangles and then add them to find the area of the given quadrilateral.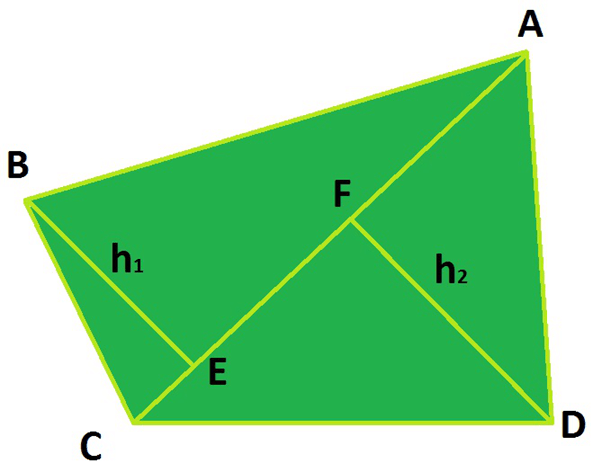
Area of quadrilateral = (Area of Triangle)1 + (Area of Triangle)2
In the above figure, the diagonal AC will act as a common base of the two triangles ABC and ADC with heights h1 and h2 respectively.
Area of quadrilateral (ABCD) = Area of Triangle (ABC) + Area of Triangle (ACD)
Area of quadrilateral (ABCD) = (1/2) x AC x h1 + (1/2) x AC x h2
Area of quadrilateral (ABCD) = (1/2) x AC x (h1 + h2)
Similarly, to find the area of a Pentagon, Hexagon, Heptagon, and Octagon or for any other polygon, we will divide the polygon into different figures and then add the area of each figure to calculate the area of the polygon.
Here, we are taking an example of a pentagon ABCDE and we will find its area by dividing it into four parts.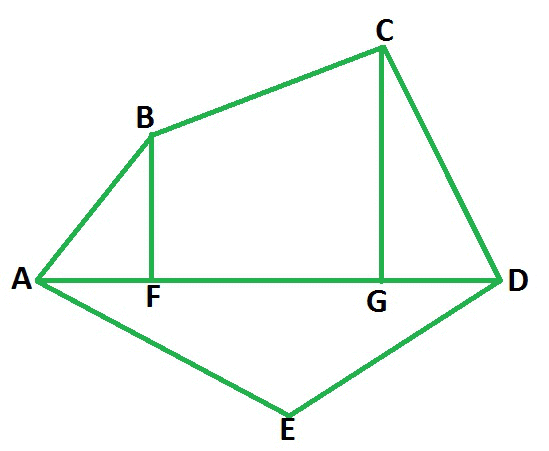
By constructing one diagonal AD and two perpendiculars BF and CG on it, pentagon ABCDE is divided into four parts. So,
Area of Pentagon (ABCDE) = Area of right angled ∆ AFB + Area of trapezium (BFGC) + Area of right angled ∆ CGD + Area of ∆ AED
Similarly, we can find the area of any polygon by dividing the polygon into different parts.
Sample Problems
Now, we will do some questions related to finding the area of polygon and this will help us clear the concept in a much better manner.
Question 1: Find the area of the given polygon.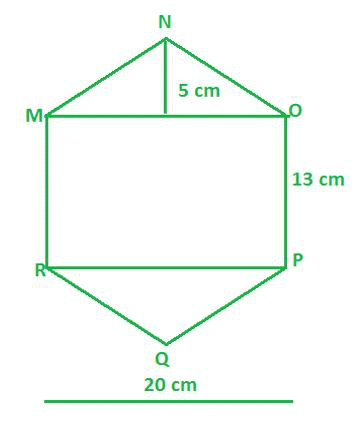
Solution:
We are given the above figure which is a Hexagon and we are supposed to find out the area of the above figure MNOPQR.
Area of the figure MNOPQR = Area of triangle MNO + Area of triangle PQR + Area of rectangle MOPR
Area of the figure MNOPQR = (1/2) × MO × NK +(1/2) × PR × QL + PO × MO
Area of the figure MNOPQR = (1/2) × 20 × 5 + (1/2) x 20 × 5 + 13 × 20
Area of the figure MNOPQR = 10 × 5 + 10 × 5 + 260
Area of the figure MNOPQR = 50 cm2+ 50 cm2 + 260 cm2
Area of the figure MNOPQR = 360 cm2
Hence, the area of the given Hexagon MNOPQR is 360 cm2.
What is a Quadrilateral?
Before going into the calculation of area, let us define what is a quadrilateral. A quadrilateral is a four-sided polygon, having the sum of interior angles equal to 360o.
Properties of Quadrilateral
- Every quadrilateral has 4 vertices and 4 sides enclosing 4 angles.
- The sum of its interior angles is 360 degrees.
- A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, parallelograms, etc. are special types of quadrilaterals with some of their sides and angles being equal.
Area of Quadrilateral Formula
Consider a quadrilateral PQRS, of different(unequal) lengths, let us derive a formula for the area of a quadrilateral.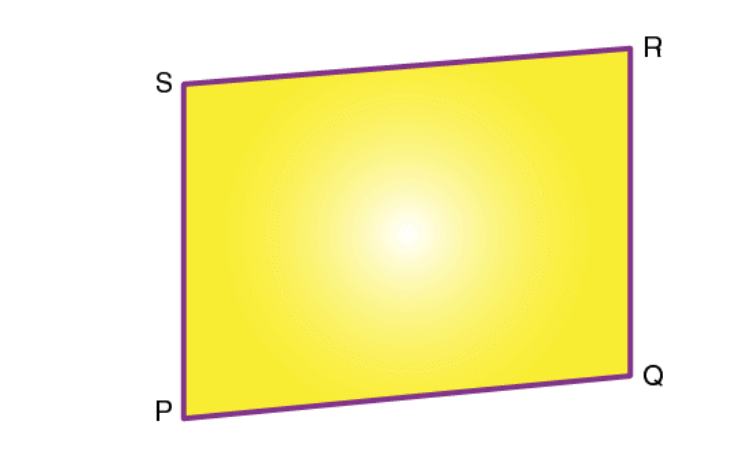
- We can view the quadrilateral as a combination of 2 triangles, with the diagonal PR being the common base.
- h1 and h2 are the heights of triangles PSR and PQR respectively.
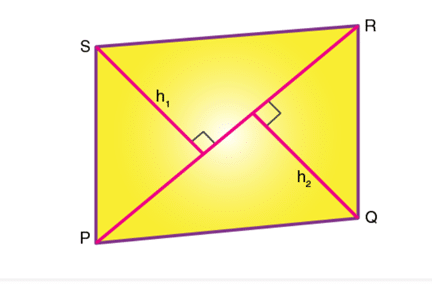
- Area of quadrilateral PQRS is equal to the sum of the area of triangle PSR and the area of triangle PQR.
- Area of triangle PSR = (base * height)/2 = (PR * h1)/2
- Area of triangle PQR = (base * height)/2 = (PR* h2)/2
- Thus, area of quadrilateral PQRS is,
- Area of triangle PSR + Area of triangle
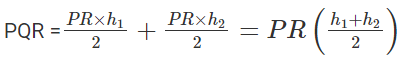
Hence, the area of a quadrilateral formula is,
Area of a general Quadrilateral = 1/2 × diagonal × (Sum of height of two triangle)
Area of a Quadrilateral Example
Question: In the given quadrilateral ABCD, the side BD = 15 cm and the heights of the triangles ABD and BCD are 5 cm and 7 cm respectively. Find the area of the quadrilateral ABCD.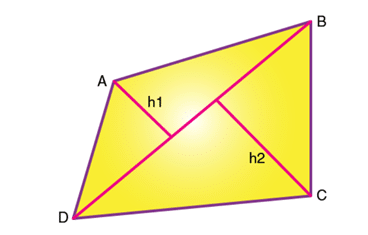
Solution:
Diagonal = BD = 15 cm
Heights, h1 = 5cm & h2 = 7cm
Sum of the heights of the triangles = h1 + h2 = 5 + 7 = 12 cm
Thus, area of quadrilateral ABCD =
= 1/2 × diagonal × (Sum of height of two triangle)
= (15 * 12)/2 = 90 cm2
|
81 videos|423 docs|31 tests
|
FAQs on Areas of Trapezium, Polygons & General Quadrilaterals - Mathematics (Maths) Class 8
| 1. What is the formula for calculating the area of a trapezium? |  |
| 2. How do you find the area of an irregular polygon? |  |
| 3. What is the difference between a polygon and a quadrilateral? |  |
| 4. Can the area of a general quadrilateral be calculated using a specific formula? |  |
| 5. What is the significance of knowing how to calculate the area of trapeziums and polygons in real life? |  |





















