Q1:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Let A and B be two independent events.
Assertion : If P (A) = 0.3 and P (A ∪ 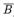 ) = 0.8, then P (B) is 2/7.
) = 0.8, then P (B) is 2/7.
Reason : P (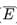 ) = 1 - P(E), where E is any event.
) = 1 - P(E), where E is any event.
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
P(A∪B′) = P(A) + P(B′) − P(A)P(B′)
∴ 0.8 = 0.3 + P(B′) − 0.3P(B′)
⇒ 0.5 = P(B′)(0.7)
⇒ P(B′) = 57
∴ P(B) = 1 − 57
= 2/7
Report a problem
Q2:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : When two coins are tossed simultaneously then the probability of getting no tail is 1/4.
Reason : The probability of getting a head (i.e., no tail) in one toss of a coin is 1/2.
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A). Probability of getting no tail when two coins tossed simultaneously i.e., both are heads.
Probability of both head
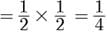
Report a problem
Q3:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion: If the probability of an event is P then probability of its complementary event will be 1 - P.
Reason: When E and 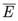 are complementary events, then P (E) + P(
are complementary events, then P (E) + P(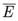 ) = 1.
) = 1.
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A). Both statements are correct and Reason is the correct for Assertion.
Since, probability of an event + probability of its complementary event = 1
So, probability of its complementary event = (1 – Probability of an event) = 1 – P.
Report a problem
Q4:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : In a simultaneous throw of a pair of dice. The probability of getting a double is 1/6.
Reason: Probability of an event may be negative.
Explanation
Assertion (A) is true but reason (R) is false. When two dice are tossed. Total possible outcomes = 36
n(S) = 36
and total favourable outcomes (doublet)
= {(1,1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
n (E) = 6
Probability = 6/36 = 1/6 and, we know that 0 ≤ P(E) ≤ 1.
Report a problem
Q5:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : The probability of winning a game is 0.4, then the probability of losing it, is 0.6
Reason : P(E) + P(not E) = 1
Explanation
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
We have, P(E) = 0.4,
where E = event of winning
P(Not E) = 1 - P(E) = 1 - 0.4 = 0.6
Report a problem
Q6:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : Cards numbered as 1, 2, 3 .......... 15 are put in a box and mixed thoroughly, one card is then drawn at random. The probability of drawing an even number is 1/2.
Reason : For any event E, we have 0 ≤ P(E) ≤ 1
Explanation
Assertion (A) is false but reason (R) is true. Total possible outcomes = 15
n(S) = 15
Total favourable numbers are 2, 4, 6, 8, 10, 12, 14.
E = {2, 4, 6, 8, 10, 12, 14}
n(E) = 7
Probability of drawing an even number = 7/15
Report a problem
Q7:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion : If E and F are events such that P(E) = 1/4, P(F) = 1/2 and P(E and F) = 1/8, then P (E or F) is 5/8.
Reason : If A and B are independent, then P (A ∩ B) = P (A).
Explanation
Assertion (A) is true but reason (R) is false.
P (E or F) = P (E ∪ F)
= P(E) + P(F) - P(E ∩ F)
= 1/4 + 1/2 - 1/8 = 5/8
Report a problem
Q8:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:Assertion: The probabilities that A, B, C can solve a problem independently are 1/3, 1/3 and 1/4 respectively. The probability that only two of them are able to solve the problem is 7/36.
Reason : If A and B are mutually exclusive events, then P(A ∩ B) ≠ 0.
Explanation
Assertion (A) is true but reason (R) is false.
1. A and B solve the problem and C does not solve the problem
2. B and C solve the problem and A does not solve the problem and
3. C and A solve the problem and B does not solve the problem. The required probability
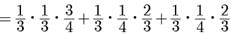
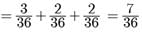
Report a problem
Q9:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If P(F) = 0.20, then the probability of ‘not E’ is 0.80.
Reason (R): If two dice are thrown together, then the probability of getting a doublet is 5/6.
Explanation
In case of assertion
P(E) = 0.20
∴ P(not E) = 1 – P(E)
= 1 – 0.20
= 0.80
∴ Assertion is correct.
In case of reason:
Total number of possible outcomes = 62 = 36
E : (doublets are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
No. of favourable outcomes to E = 6
∴ P(a doublet)
= Number of outcomes favourable to E/Total number of outcomes
= 6/36 = 1/6
∴ Reason is incorrect:
Hence, the assertion is correct but the reason is incorrect.
Report a problem
Q10:
Question for Assertion & Reason Type Questions: Probability
Try yourself: Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): The probability that a number selected at random from the number 1, 2, 3, ......., 15 is a multiple of 4, is 1/3.
Reason (R): Two different coins are tossed simultaneously. The probability of getting at least one head is 3/4.
Explanation
In case of assertion
n(S) = 15
n(A) = 3
p(A) = n(A)/n(S) = 3/15 = 1/5.
∴ Assertion is incorrect.
In case of reason:
S = HH, HT, TH, TT
A = HH, HT, TH
n(S) = 4
n(A) = 3
∴ p(A) = n(A)/n(S) = 3/4.
∴ Reason is correct:
Hence, the assertion is incorrect but the reason is correct.
Report a problem
![]() ) = 0.8, then P (B) is 2/7.
) = 0.8, then P (B) is 2/7.![]() ) = 1 - P(E), where E is any event.
) = 1 - P(E), where E is any event.![]() are complementary events, then P (E) + P(
are complementary events, then P (E) + P(![]() ) = 1.
) = 1.















