Assumed Mean to Statistics | Additional Topics for IIT JAM Mathematics PDF Download
Assumed Mean:-
In the section on averages, we learned how to calculate the mean for a given set of data. The data we looked at was ungrouped data and the total number of elements in the data set was not that large. That method is not always a realistic approach especially if you're dealing with grouped data.
That's where the assumed mean comes into play.
Assumed mean, like the name suggests, is a guess or an assumption of the mean. Assumed mean is most commonly denoted by the letter a. It doesn't need to be correct or even close to the actual mean and choice of the assumed mean is at your discretion except for where the question explicitly asks you to use a certain assumed mean value.
Assumed mean is used to calculate the actual mean as well as the variance and standard deviation as we'll see later.
Assumed mean can be calculated from the following formula: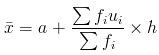
It's very important to remember that the above formula only applies to grouped data with equal class intervals.
Now let us define each term used in the formula:
- x̄ is the mean which we're trying to find.
- a is the assumed mean.
- h is the class interval which we looked at in the section on data.
- fi is the frequency of each class, we find the total frequency of all the classes in the data set (∑fi) by adding up all the fi 's
- Each ui is found from the following formula:
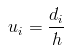
where h is the class interval and each di is the difference between the mid element in a class and the assumed mean.
d is calculated from the following formula: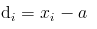
where x is the midpoint of a given class.
x is obtained from the following: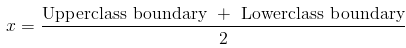
xi is the number in the middle of a given class.
Therefore ui becomes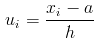
Let's try an example to see how to apply the assumed mean method for finding mean.
Example 1: The student body of a certain school were polled to find out what their hobbies were. The number of hobbies each student had was then recorded and the data obtained was grouped into classes shown in the table below. Using an assumed mean of 17, find the mean for the number of hobbies of the students in the school.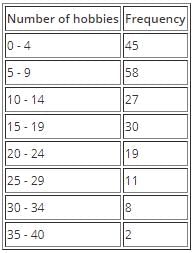
Solution: We have been given the assumed mean a as 17 and we know the formula for finding mean from the assumed mean as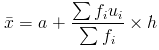
we can find the class interval by using the class limits as follows: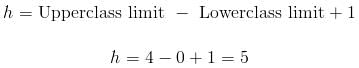
We now have one component we need and we're one step closer to finding the mean.
So we can solve the rest of this problem using a table where by we find each remaining component of the formula and then substitute at the end:
substituting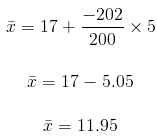
The mean number of hobbies is 11.95.
|
2 videos|45 docs|4 tests
|
















