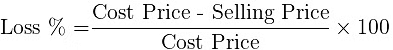Basic Concept: Profit, Loss & Discount | General Aptitude for GATE - Mechanical Engineering PDF Download
| Table of contents |

|
| Introduction |

|
| Profit, Loss, and Discount |

|
| Basic Concepts and Formulas |

|
| Some Solved Problems |

|
Introduction
The profit and Loss formula is used in mathematics to determine the price of a commodity in the market and understand how profitable a business is.

- Every product has a cost price and a selling price.
- Based on the values of these prices, we can calculate the profit gained or the loss incurred for a particular product.
Profit, Loss, and Discount
1. Cost Price (CP)
The amount paid for a product or commodity to purchase it is called a cost price. Also, denoted as CP.
This cost price is further classified into two different categories:
- Fixed Cost: The fixed cost is constant, it doesn’t vary under any circumstances
- Variable Cost: It could vary depending as per the number of units
2. Selling price (SP)
- The amount for which the product is sold is called Selling Price. It is usually denoted as SP. Also, sometimes called a sale price.
3. Profit and Loss
Profit: When an article is sold for more than the cost of the article, then we say there is a Profit or Gain.
- Profit or Gain = S.P - C.P
Loss: When an article is sold for less than the cost of the article, then we say there is a Loss.
- Loss = C.P - S.P
The formula for the profit and loss percentage is:
- Profit percentage = (Profit / Cost Price) x 100
- Loss percentage = (Loss / Cost price) x 100
4. Marked Price Formula (MP)
This is basically labeled by shopkeepers to offer a discount to the customers in such a way that,
- Discount = Marked Price – Selling Price
- Discount Percentage = (Discount/Marked price) x 100
Basic Concepts and Formulas

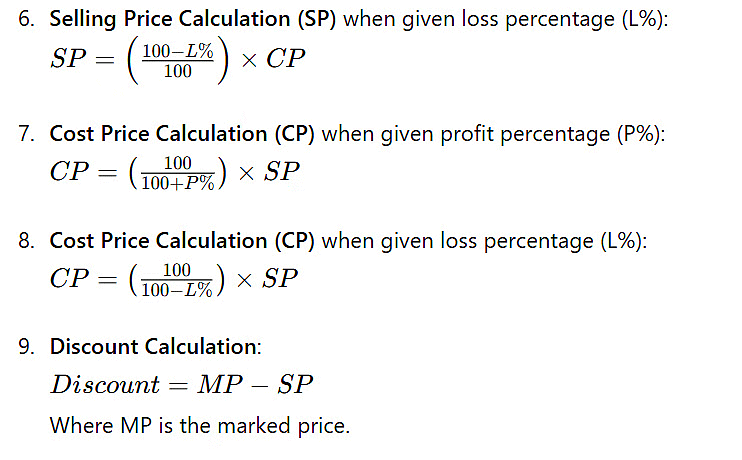
Specific Cases and Rules
- False Weight Calculation: If a product is sold at a false weight, the profit percentage is calculated based on the difference between the true weight and the false weight:
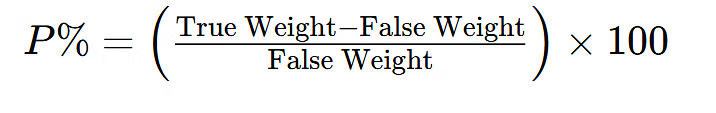
- Net Percentage Profit: when there are two successive profits:
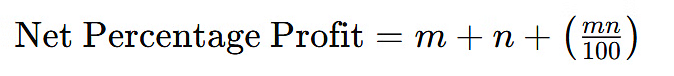 Where and are the percentages of the two successive profits.
Where and are the percentages of the two successive profits. - Net Percentage Profit or Loss when there's a profit and a loss:
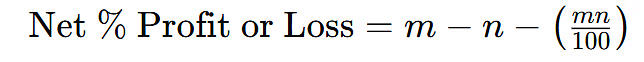 Where is the profit percentage and is the loss percentage.
Where is the profit percentage and is the loss percentage. Effective Cost Price Calculation after successive profits:
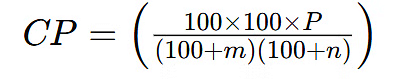 Where is the final selling price after two successive profits.
Where is the final selling price after two successive profits.
Some Solved Problems
To understand the concept let's first open a shop say a local retail stationery shop.
Example 1: Now suppose a student shows up and wants to buy 5 gel pens worth ₹ 5 each. The cost price of one pen is ₹ 4. So, what is the profit earned by the shopkeeper in net terms and its profit percentage?
This ₹ 5 is the selling price, the price at which the commodity is sold to its buyer. And ₹ 4 is the price at which the shopkeeper has bought these pens from his supplier and this price is known as Cost Price.
Thus, this difference between the price at which the shopkeeper buys his pen and at which it is sold is known as profit/ loss earned. Now if Selling Price > Cost Price then he will earn profit and if Selling Price < Cost Price, then he will earn loss.
Therefore, Profit = Selling Price – Cost Price = ₹ 5 – ₹4 = ₹1 per pen
Now,i.e.
And consequently, Loss = Cost Price – Selling Pricei.e.
Example 2: Suppose another customer comes to the shop and bought 2 registers worth ₹ 50 each and a pencil box from him. And this time the shopkeeper has earned 40% profit on the registers. He earned a profit of ₹10 on pencil box and the profit% on pencil box is 20%. Then what is the cost price and profit on register and selling price and cost price of pencil box?
In this case, we are given S.P. = ₹ 50 for each register and profit% = 40%. Let C.P. be x.
⇒ Profit % = {(50 – x)/x} * 100
⇒ 40 = {(50 – x)/x} * 100
⇒ 4x = 500 – 10x
⇒ 14x = 500
⇒ x = 35.71
⇒ Profit = 50 – 35.71 = 14.29What if the profit of 40% is on selling price instead?
⇒ Profit = profit% * S.P = 0.4* 50 = ₹20
C.P. = S.P. – Profit = ₹50 – ₹20 = ₹30Let's now move on to calculate S.P. and C.P. of pencil box. Let C.P. of pencil box be y
∵ Profit % = (profit/ Cost price) *100
⇒ 20 = (10/y) *100
⇒ 2y = 100
⇒ y = ₹ 50
Therefore, S.P. = ₹50 + ₹10 = ₹60
Example 3: Since not many customers showed up on the first day of the shop. Therefore, to popularize the shop the shopkeeper puts up discount of 20% on all the products. The first customer shows up and bought a packet of pencils and 3 erasers and still making up the profit of 30% on both the items. Then what is the actual cost price of both the items when the pencil is marked as ₹30 and the eraser ₹ 5 each?
What does the underlined marked mean?
Here marked means Marked Price is the price that is offered to customer before discount basically, discount is just difference between marked price and Selling price i.e. Discount = M.P. – S.P.
In this case, Discount = 0.2 * Price of packet of pencil = 0.2 *30 = ₹ 6
Therefore, S.P = 30 – 6 = ₹ 24
∵ Profit is 30% on C.P., assume C.P. be x
⇒ 0.3 = (24 – x)/x
⇒ 0.3x = 24 – x
⇒ 1.3x = 24
⇒ x = 18.46
Similarly,
Discount = 0.2 * Price of 3 erasers = 0.2* 3*5 = ₹ 3
Hence, S.P. = (3*5) - 3 = ₹ 12
∵ Profit is 30% on C.P., assume C.P. be y
⇒ 0.3 = (12 – y)/y
⇒ 1.3y = 12
⇒ y (C.P. of 3 eraser) = 9.23
Example 4: Consider this situation, that the stationery sold a parker pen at a loss of 20% for ₹ 100 and a pack of colored sketch pens at the loss of 15% on S.P. What are the cost price and selling price of both the articles?
First, let's find out the C.P. and S.P. parker pen,
∵ Loss is 20% on C.P.
Let C.P. be x and S.P. be 100
⇒ S.P. = 0.8 of C.P.
⇒ 100 = 0.8x
⇒ 100/0.8 = x
⇒ 125 = x
For sketch pens,
∵ Loss is 15% on S.P.
Let S.P. be y and C.P. be 100
⇒ Loss = 0.15y
⇒ C.P. = 1.15 y
⇒ 100 = 1.15y
⇒ 100/1.15 = y
⇒ y = ₹ 87
Example 5: A watch dealer incurs an expense of Rs. 150 for producing every watch. He also incurs an additional expenditure of Rs. 30,000, which is independent of the number of watches produced. If he is able to sell a watch during the season, he sells it for Rs. 250. If he fails to do so, he has to sell each watch for Rs. 100. If he is able to sell only 1,200 out of 1,500 watches he has made in the season, then he has made a profit of:
(a) ₹ 90000
(b) ₹ 75000
(c) ₹ 45000
(d) ₹ 60000
Here, first find out cost he has incurred to produce the watches.
∵ He made 1500 watches costing ₹ 150 each and an additional ₹ 30000 expense on them.
⇒ Total Cost = (1500*150) + 30000 = ₹ 255000
∵ He's able to sell 1200 watches in the season = ₹250 each
So, the revenue earned by him during the season = ₹250 * 1200 = ₹ 300000
Also, the leftover 300 pieces of clocks would have been sold by the watchmaker in off-season = 100 each.
Revenue earned through these 300 watches = 300*100 = ₹ 30000
Total Revenue = ₹ 300000 + ₹30000 = ₹330000
Profit = Revenue - Cost = 330000 - 255000 = ₹ 75000
Example 6: Instead of a meter scale, a cloth merchant uses a 120cm scale while buying, but uses an 80cm scale while selling the same cloth. If he offers a discount of 20% on cash payment, what is his overall profit percentage?
This question above is a special one with the faulty dealer. Here, the dealer is earning profit by using a false scale.
To solve this problem, first assume that the price of the cloth is ₹ 1/cm
∵ He's using a 120 cm scale.
⇒ C.P. = (100/120) * ₹1 = ₹ 0.8333/cm
∵ This merchant again uses faulty scale to sell the cloth to his customers. He uses a scale that measures 80cm as 100cm i.e. he sells 80cm for ₹100
Now he also gives a discount of 20% on the cloth.
⇒ His mark up price is ₹100/80cm
∵ S.P. = M.P. - M.P. * Discount% = M.P. (1 - Discount%) = (100/80)*(80/100) = ₹1/cm
Therefore, his profit % = (1 – 0.8333)/0.8333 *100 = 20%
|
193 videos|169 docs|152 tests
|
FAQs on Basic Concept: Profit, Loss & Discount - General Aptitude for GATE - Mechanical Engineering
| 1. What are the basic concepts related to profit, loss, and discount? |  |
| 2. What are the common formulas used in calculating profit, loss, and discount? |  |
| 3. Can you provide an example of a solved problem involving profit, loss, and discount? |  |
| 4. How are profit, loss, and discount important in business and financial transactions? |  |
| 5. How can a better understanding of profit, loss, and discount help in making informed financial decisions? |  |