Basics of Probability | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| Introduction |

|
| Basic Terminologies |

|
| Theorems |

|
| Total Law of Probability |

|
| PYQs: Competitive Exams |

|
Introduction
Probability refers to the extent of occurrence of events. When an event occurs like throwing a ball, picking a card from deck, etc ., then the must be some probability associated with that event.
In terms of mathematics, probability refers to the ratio of wanted outcomes to the total number of possible outcomes. There are three approaches to the theory of probability, namely:
- Empirical Approach
- Classical Approach
- Axiomatic Approach
In this, we are going to study about axiomatic approach. In this approach, we represent the probability in terms of sample space(S) and other terms.
Basic Terminologies
- Random Event: If the repetition of an experiment occurs several times under similar conditions, if it does not produce the same outcome everytime but the outcome in a trial is one of the several possible outcomes, then such an experiment is called random event or a probabilistic event.
- Elementary Event: The elementary event refers to the outcome of each random event performed. Whenever the random event is performed, each associated outcome is known as elementary event.
- Sample Space: Sample Space refers to the set of all possible outcomes of a random event. Example, when a coin is tossed, the possible outcomes are head and tail.
- Event: An event refers to the subset of the sample space associated with a random event.
- Occurrence of an Event: An event associated with a random event is said to occur if any one of the elementary event belonging to it is an outcome.
- Sure Event: An event associated with a random event is said to be sure event if it always occurs whenever the random event is performed.
- Impossible Event: An event associated with a random event is said to be impossible event if it never occurs whenever the random event is performed.
- Compound Event: An event associated with a random event is said to be compound event if it is the disjoint union of two or more elementary events.
- Mutually Exclusive Events: Two or more events associated with a random event are said to be mutually exclusive events if any one of the event occurrs, it prevents the occurrence of all other events. This means that no two or more events can occur simultaneously at the same time.
- Exhaustive Events: Two or more events associated with a random event are said to be exhaustive events if their union is the sample space.
- Probability of an Event: If there are total p possible outcomes associated with a random experiment and q of them are favourable outcomes to the event A, then the probability of event A is denoted by P(A) and is given by
P(A) = q / p
The probability of non occurrence of event A, i.e, P(A’) = 1 – P(A)
Note:
- If the value of P(A) = 1, then event A is called sure event .
- If the value of P(A) = 0, then event A is called impossible event.
- Also, P(A) + P(A’) = 1
Theorems
1. General: Let A, B, C are the events associated with a random experiment, then
- P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
- P(A ∪ B) = P(A) + P(B) if A and B are mutually exclusive
- P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C)- P(C ∩ A) + P(A ∩ B ∩ C)
- P(A ∩ B’) = P(A) – P(A ∩ B)
- P(A’ ∩ B) = P(B) – P(A ∩ B)
2. Extension of Multiplication Theorem: Let A1, A2, ….., An are n events associated with a random experiment, then
P(A1∩A2∩A3 ….. An) = P(A1)P(A2 / A1)P(A3 / A2 ∩ A1) ….. P(An / A1 ∩ A2 ∩ A3 ∩.. ∩ An - 1)
Example 1: A bag contains 10 oranges and 20 apples out of which 5 apples and 3 oranges are defective .If a person takes out two at random, what is the probability that either both are good or both are apples ?
Solution:
Out of 30 items, two can selected in 30C2 ways .
Thus, Total elementary events = 30C2 .
Consider the events :
A = Getting two apples
B = Getting two good items
Required Probability is:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) …(i)
There are 20 apples, out of which 2 can be drawn in 20C2 ways .
P(A) = 20C2 / 30C2
There are 8 defective items and 22 are good, Out of 22 good items, two can be can drawn in 22C2 ways.
P(B) = 22C2 / 30C2
Since there are 15 items which are good apples, out of which 2 can be selected in 15C2 ways.
P(A∩B) = 15C2 / 30C2
Substituting the values of P(A), P(B) and P(A∩B) in (i)
Required probability is = (20C2 / 30C2) + (22C2 / 30C2) – (15C2 / 30C2) = 316/435
Example 2: The probability that a person will get an electric contract is 2/5 and probability that he will not get plumbing contract is 4/7 . If the probability of getting at least one contact is 2/3, what is the probability of getting both?
Solution:
Consider the two events:
A = Person gets electric contract
B = Person gets plumbing contract
We have,
P(A) = 2 / 5
P(B’) = 4 / 7
P(A ∪ B) = 2 / 3
Now,
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= (2 / 5) + (1 – 4 / 7) – (2 / 3) = 17 / 105
Total Law of Probability
Let S be the sample space associated with a random experiment and E1, E2, …, En be n mutually exclusive and exhaustive events associated with the random experiment. If A is any event which occurs with E1 or E2 or … or En, then
P(A) = P(E1)P(A / E1) + P(E2)P(A / E2) + ... + P(En)P(A / En)
Example 1: A bag contains 3 black balls and 4 red balls. A second bag contains 4 black balls and 2 red balls. One bag is selected at random. From the selected bag, one ball is drawn. Find the probability that the ball drawn is red.
Solution:
A red ball can be drawn in two ways:
Selecting bag I and then drawing a red ball from it.
Selecting bag II and then drawing a red ball from it.
Let E1, E2 and A be the defined events as follows:
E1 = Selecting bag I
E2 = Selecting bag II
A = Drawing red ball
Since selecting one of the two bags at random.
P(E1) = 1 / 2
P(E2) = 1 / 2
Now, probability of drawing red ball when first bag has been chosen
P(A / E1) = 4 / 7
and, probability of drawing red ball when second bag has been chosen
P(A / E2) = 2 / 6
Using total law of probability, we have
P(A) = P(E1)P(A / E1) + P(E2)P(A / E2)
= (1 / 2)(4 / 7) + (1 / 2)(2 / 6)
= 19 / 42
Hence, the probability of drawing a red ball is 19 / 42
Example 2: In a bulb factory, three machines namely A, B, C produces 25%, 35% and 40% of the total bulbs respectively. Of their output, 5, 4 and 2 percent are defective bulbs respectively. A bulb is drawn is drawn at random from products. What is the probability that bulb drawn is defective ?
Solution:
Let E1, E2, E3 and A be the defined events as follows:
E1 = The bulb is manufactured by machine A
E2 = The bulb is manufactured by machine B
E3 = The bulb is manufactured by machine C
A = The bulb is defective
According to given conditions;
P(E1) = 25 / 100
P(E2) = 35 / 100
P(E3) = 40 / 100
Now, probability that the bulb is defective given that is produced by Machine A
P(A / E1) = 5 / 100
and, probability that the bulb is defective given that is produced by Machine B
P(A / E2) = 4 / 100
and, probability that the bulb is defective given that is produced by Machine C
P(A / E3) = 2 / 100
Using total law of probability, we have
P(A) = P(E1)P(A / E1) + P(E2)P(A / E2) + P(E3)P(A / E3)
= (25 / 100)(5 / 100) + (35 / 100)(4 / 100) + (40 / 100)(2 / 100)
= 0.0345
Hence, the probability that the bulb is defective is 0.0345.
PYQs: Competitive Exams
Q1: The figure below shows the front and rear view of a disc, which is shaded with identical patterns. The disc is flipped once with respect to any one of the fixed axes 1-1, 2-2 or 3-3 chosen uniformly at random.
What is the probability that the disc DOES NOT retain the same front and rear views after the flipping operation?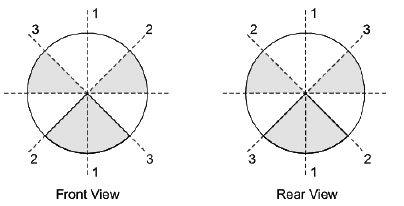
(a) 0
(b) 1/3
(c) 2/3
(d) 1
Ans: c
Sol:
n = Total = 3
m = Favourable = disc does not retain the same front and rear views after the flipping = 2
Probability = m/n = 2/3
Q2: There are two identical dice with a single letter on each of the faces. The following six letters : Q, R, S, T, U and V, one on each of the faces. Any of the six outcomes are equally likely.
The two dice are thrown once independently at random.
What is the probability that the outcomes on the dice were composed only of any combination of the following possible outcomes : Q, U and V?
(a) 1/4
(b) 3/4
(c) 1/6
(d) 5/36
Ans: a
Sol:
Given two dice.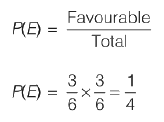
Q3: Suppose the probability that a coin toss shows “head” is p, where 0 < p < 1. The coin is tossed repeatedly until the first “head” appears. The expected number of tosses required is
(a) (1-p)/p
(b) 1/p
(c) 1/p2
(d) p/(1-p)
Ans: b
Sol:
|
65 videos|129 docs|94 tests
|
FAQs on Basics of Probability - Engineering Mathematics - Engineering Mathematics
| 1. What are the basic terminologies in probability? |  |
| 2. What is the Total Law of Probability? |  |
| 3. What are some important theorems in probability? |  |
| 4. What is the sample space in probability? |  |
| 5. What is a random variable in probability? |  |
















