Binary Arithmetic | Analog and Digital Electronics - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Binary Arithmetic Basics |

|
| Binary Equivalent of Decimal Numbers |

|
| Binary Addition |

|
| Binary Subtraction |

|
| Binary Multiplication |

|
| Binary Division |

|
| Signed Binary Numbers |

|
| Arithmetic Overflow |

|
Binary Arithmetic Basics
- Binary arithmetic means doing math using only two numbers: 0 and 1. It's like regular math, but instead of using numbers like 1, 2, 3, and so on, we only use 0 and 1.
- We have rules, like truth tables, for adding, subtracting, multiplying, and dividing these binary numbers. We use these rules to perform basic calculations.
- Before we dive into how binary arithmetic works, let's quickly review how we represent regular numbers in binary form.
Binary Equivalent of Decimal Numbers
Below is a chart showing how decimal numbers are represented in binary.
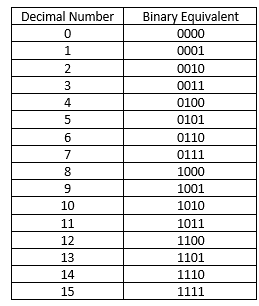
Binary Equivalent of Decimal Numbers
- In this representation, we use four positions to represent decimal numbers in base two. With these four positions, we can represent numbers from 0 to 15. To find the binary equivalent, we use the powers of two. To find the decimal equivalent, we multiply each digit by the appropriate power of two. Let's look at an example.

Binary Weightage
- In the example above, we found the decimal equivalent of 1010. To do this, we multiplied each digit by the powers of two. In the binary number 1010, the rightmost digit is the least significant bit (LSB), and the leftmost digit is the most significant bit (MSB). We start from the right and multiply each digit by two to the power of zero, then two to the power of one, and so on.
- Finally, we add all these values together to get the decimal equivalent. So, the decimal equivalent of 1010 is 10 (ten), as shown in the chart. Similarly, we can find the decimal equivalent of any binary number. As mentioned earlier, with four positions, we can represent numbers from 0 to 15, and with six positions, we can represent numbers from 0 to 63, and so on.
Binary Addition
Binary addition is about adding two binary numbers together. Here's how it works:

Binary Addition Truth Table
- When you add two low bits (0 + 0), the result is always low (0). This means adding two zeros doesn't change the overall value.
- When you add a low bit to a high bit (0 + 1) or a high bit to a low bit (1 + 0), the result is always high (1). This means whenever you add 0 to 1 or 1 to 0, the sum is 1. And in these cases, there's no carry.
- When you add two high bits (1 + 1), the result is high (1), but with a carry. This means when you add two ones together, the sum is 0 with a carry of 1.
Here are the rules for binary addition:
- Start from the rightmost bit (also called the LSB).
- When adding a low bit with a low bit, the result is low.
- When adding a high bit with a low bit or vice versa, the result is high.
- When adding two high bits, the result is high with a carry of 1.
Let's look at an example to understand this better. Take a look at the table below:
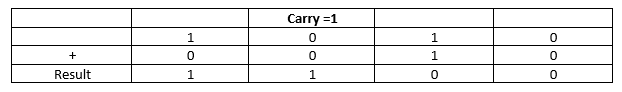
Binary Addition Example
In this example, we start from the rightmost bit (LSB). First, we add 0 to 0, which gives us 0 with no carry. Then, we move to the next bit. When we add 1 to 1, according to the truth table, the sum is 0, but there's a carry of 1 from the previous step. Next, we add 0 to 0 again, with the carry from the previous step.
So, the sum is 1, with no carry. Finally, we add 1 to 0, resulting in 1. We can double-check our answer. We're adding (1010) to (0010), whose decimal equivalents are 10 and 2, giving us the solution 12. And the decimal equivalent of 12 is 1100, as shown in the table. Therefore, our calculation is correct.
Binary Subtraction
Here's the truth table for binary subtraction:
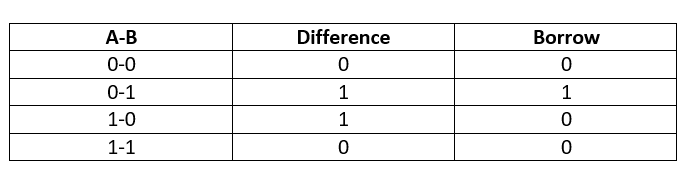 Binary Subtraction Truth Table
Binary Subtraction Truth Table
When we subtract two binary numbers, we get two outputs: the difference and the borrow.
Here's how it works:
- If we subtract a low bit from another low bit, the output is low. There's no change in the overall value.
- If we try to subtract a high bit from a low bit, it's not possible without borrowing. In this case, both the difference and borrow are high. This is similar to what we do in regular subtraction.
- When a low bit is subtracted from a high bit, the difference is high, and there's no need for borrowing.
- When we subtract two high bits, the difference is low. Except for the case where we need to borrow, the borrow is always zero.
Let's consider an example using the table below:
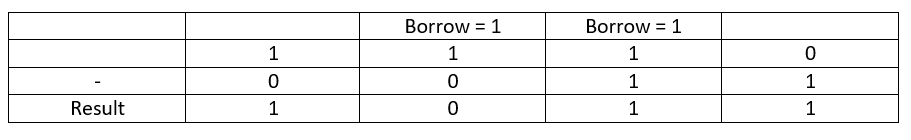
Binary Subtraction Example
In this example, we're subtracting 1110 from 0011. Just like in addition, we start from the least significant bit. So, we start with 0 minus 1. Since we can't subtract a low bit from a high bit without borrowing, we borrow and the difference becomes 1. Then, we have two ones, so we subtract 1 from 1, resulting in 0. Then, we subtract the difference from 1, which gives us 1 with a borrow. In the third step, we've borrowed 1, and the bits are 1 and 0. So, the difference is 0 with no borrow. Lastly, we have 1 subtracted from 1, resulting in 0 with no borrow.
We can double-check our answer. The decimal equivalent of 1110 is 14, and the decimal equivalent of 0011 is 2. So, the difference should be 11. Checking the result, we get 1011, which is indeed the binary equivalent of 12. This confirms that our subtraction is correct. Now, let's move on to the next binary operation.
Binary Multiplication
The truth table for binary multiplication is shown below:

Binary Multiplication Truth Table
The rules for binary multiplication are straightforward. When both inputs are low, the output is low. When one input is low and the other is high, the output is low. The output is high only when both inputs are high. Here's an example of binary multiplication:
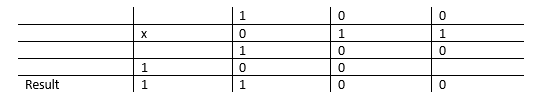
Binary Multiplication Example
In the example above, we multiply 100 (which is equivalent to 4 in decimal) by 011 (which is equivalent to 3 in decimal). This gives us the result 1100 (which is equivalent to 12 in decimal). Binary multiplication combines both binary addition and binary multiplication. It's essentially the same as how we do multiplication in regular decimal arithmetic.
Binary Division
Here's the truth table for binary division:
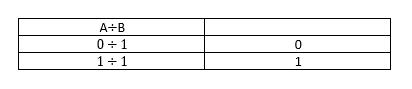
Binary Division Truth Table
Binary division only has two cases because you can't divide any number by 0, and dividing 0 by 0 is undefined. So, as shown, we only have two cases. When a low number is divided by a high number, the output is low, and when a high number is divided by another high number, the output is high. Here's an example illustrating binary division:
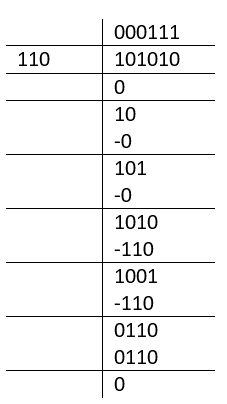
Binary Division Example
In this example, we divide 101010 (which is equivalent to 42 in decimal) by 110 (which is equivalent to 6 in decimal). The result is 111 (which is equivalent to 7 in decimal), with no remainder.
So, we've covered the four basic binary arithmetic operations, including truth tables and solved examples. All these operations can be implemented using logic gates. Gates like AND, OR, and Ex-OR are used to build circuits for these operations. For instance, a simple 4-bit adder circuit uses 4 bits to perform addition.
Signed Binary Numbers
Signed binary numbers enable digital systems to represent both positive and negative integers, expanding the capabilities of binary arithmetic. This section explores two common formats—sign-magnitude and two’s complement—and their theoretical significance in digital electronics.Sign-Magnitude Format: In this approach, the most significant bit serves as the sign bit (0 for positive, 1 for negative), while the remaining bits denote the magnitude. Although intuitive, this format complicates arithmetic operations due to the need for separate handling of sign and magnitude.
Two’s Complement Format: Negative numbers are represented by inverting all bits of the corresponding positive number and adding 1. This method simplifies arithmetic, as addition and subtraction can be performed using the same hardware, and it ensures a single representation for zero.
Theoretical Importance: Two’s complement is the preferred format in digital systems due to its algebraic consistency and efficiency. It supports seamless arithmetic operations in applications such as microprocessors and digital signal processing.
Arithmetic Overflow
Arithmetic overflow is a critical concept in binary arithmetic, occurring when the result of an operation exceeds the representable range of a fixed-bit number. This section examines its theoretical implications for digital system design.
Overflow arises when the outcome of addition or subtraction cannot be accurately represented within the allocated bit width. For example, in unsigned arithmetic, adding two large numbers may exceed the maximum value, while in signed arithmetic, a sign mismatch may occur.
Detection: In unsigned systems, overflow is indicated by a carry-out from the most significant bit. In signed systems (e.g., two’s complement), it is detected when the result’s sign is inconsistent with the operands’ signs.
Significance: Overflow can lead to erroneous results, making its detection vital for reliable digital circuits. System designers incorporate overflow checks to ensure computational accuracy in applications like arithmetic logic units.
|
135 videos|181 docs|71 tests
|
FAQs on Binary Arithmetic - Analog and Digital Electronics - Electrical Engineering (EE)
| 1. What is binary arithmetic? |  |
| 2. How do you convert decimal numbers to binary? |  |
| 3. What is binary addition? |  |
| 4. How do you perform binary subtraction? |  |
| 5. How do you multiply binary numbers? |  |





















