Boolean Algebra | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
Introduction
Boolean algebra is a mathematical system derived from working with binary logic. It was introduced by the English mathematician George Boole in 1854 and is essentially a variation of Aristotle's propositional logic, employing symbols such as 0 and 1 or True and False. Boolean algebra primarily deals with binary variables and logical operations.
Boolean Algebra plays a pivotal role in the advancement of digital electronics systems, as these systems rely on the principles of Boolean Algebra to carry out operations and functions.
Boolean Algebra Operations
There are various operations that are used in Boolean algebra but the basic operations that form the base of Boolean Algebra are,
- Negation or NOT Operation
- Conjunction or AND Operation
- Disjunction or OR Operation
These operations have their own symbols and precedence and the table added below shows the symbol and the precedence of these operators.
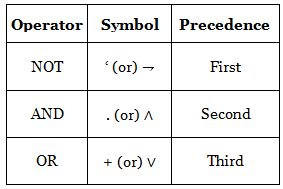 We can easily define these operations using two boolean variables. Let’s take two boolean variables A and B that can have any of the two values 0 or 1, i.e. they can be either OFF or ON. Then these operations are explained as,
We can easily define these operations using two boolean variables. Let’s take two boolean variables A and B that can have any of the two values 0 or 1, i.e. they can be either OFF or ON. Then these operations are explained as,
Negation or NOT Operation
Using the NOT operation reverse the value of the Boolean variable from 0 to 1 or vice-versa. This can be understood as:
- If A = 1, then using NOT operation we have (A)’ = 0
- If A = 0, then using the NOT operation we have (A)’ = 1
We also represent the negation operation as ~A, i.e if A = 1, ~A = 0
Conjunction or AND Operation
Using the AND operation satisfies the condition if both the value of the individual variables are true and if any of the value is false then this operation gives the negative result. This can be understood as,
- If A = True, B = True, then A . B = True
- If A = True, B = False, Or A = false, B = True, then A . B = False
- If A = False, B = False, then A . B = False
Disjunction (OR) Operation
Using the OR operation satisfies the condition if any value of the individual variables are true, it only gives a negative result if both the values are false. This can be understood as,
- If A = True, B = True, then A + B = True
- If A = True, B = False, Or A = false, B = True, then A + B = True
- If A = False, B = False, then A + B = False
Boolean Expression and Variables
Boolean expression is an expression that produces a Boolean value when evaluated, i.e. it produces either a true value or a false value. Whereas boolean variables are variables that store Boolean numbers.
P + Q = R is a Boolean phrase in which P, Q, and R are Boolean variables that can only store two values: 0 and 1. The 0 and 1 are the synonyms for false and True and are used in Boolen Algebra, sometimes we also use “Yes” in place of True and “No” in place of False.
Thus, we can say that statements using Boolean variables and operating on Boolean operations are Boolean Expressions. Some examples of Boolean expressions are,
- A + B = True
- A.B = True
- (A)’ = False
Boolean Algebra Terminologies
There are various terminologies related to Boolean Algebra, which are used to explain various parameters of Boolen Algebra. That includes,
- Boolean Algebra
- Boolean Variables
- Boolean Function
- Literal
- Complement
- Truth Table
Now, we will discuss the important terminologies of Boolean algebra in the article below,
Boolean Algebra
The branch of algebra that deals with binary operations or logical operations is called Boolean Algebra.
Boolean Variables
Variables used in Boolean algebra that store the logical value of 0 and 1 are called the boolean variables. They are used to store either true or false values.
Boolean Function
A function of the Boolean Algebra that is formed by the use of Boolean variables and Boolean operators is called the Boolean function.
Literal
A variable or the complement of the variable in Boolean Algebra is called the Literal.
Complement
The inverse of the boolean variable is called the complement of the variable. The complement of 0 is 1 and the complement of 1 is 0. It is represented by ‘ over the variable.
Truth Table
Table containing all the possible values of the logical variables and the combination of the variable along with the given operation is called the truth table. The number of rows in the truth table depends on the total boolean variables used in that function. It is given by using the formula,
- Number of Rows in Truth Table = 2n
- where “n” is the number of boolean variables used.
Truth Tables in Boolean Algebra
A truth table represents all the combinations of input values and outputs in a tabular manner. All the possibilities of the input and output are shown in it and hence the name truth table. In logic problems, truth tables are commonly used to represent various cases. T or 1 denotes ‘True’ & F or 0 denotes ‘False’ in the truth table.
Example: Draw the truth table of the conditions A + B and A.B where A and b are boolean variables.
Sol:
The required Truth Table is,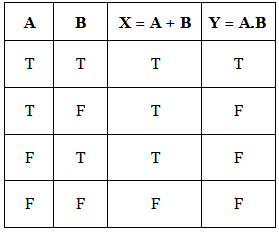
Laws for Boolean Algebra
The basic laws of the Boolean Algebra are added in the table added below,

Identity Law
In the Boolean Algebra, we have identity elements for both AND(.) and OR(+) operations. The identity law state that in boolean algebra we have such variables that on operating with AND and OR operation we get the same result, i.e.
- A + 0 = A
- A.1 = A
Commutative Law
Binary variables in Boolean Algebra follow the commutative law. This law states that operating boolean variables A and B is similar to operating boolean variables B and A. That is,
- A. B = B. A
- A + B = B + A
Associative Law
Associative law state that the order of performing Boolean operator is illogical as their result is always the same. This can be understood as,
- ( A . B ) . C = A . ( B . C )
- ( A + B ) + C = A + ( B + C)
Distributive Law
Boolean Variables also follow the distributive law and the expression for Distributive law is given as:
- A . ( B + C) = (A . B) + (A . C)
Inversion Law
Inversion law is the unique law of Boolean algebra this law states that, the complement of the complement of any number is the number itself.
- (A’)’ = A
Apart from these other laws are mentioned below:
AND Law
AND law of the Boolean algebra uses AND operator and the AND law is,
- A . 0 = 0
- A . 1 = A
- A . A = A
OR Law
OR law of the Boolean algebra uses OR operator and the OR law is,
- A + 0 = A
- A + 1 = 1
- A + A = A
De Morgan’s Laws are also called Demorgan’s Theorem. They are the most important laws in Boolen Algebra and these are added below under the heading Boolean Algebra Theorem
Boolean Algebra Theorems
There are two basic theorems of great importance in Boolean Algebra, which are De Morgan’s First Laws, and De Morgan’s Second Laws. These are also called De Morgan’s Theorems. Now let’s learn about both in detail.
De Morgan’s First laws
Statement: The complement of the product (AND) of two Boolean variables (or expressions) is equal to the sum(OR) of the complement of each Boolean variable (or expression).
(P.Q)’ = (P)’ + (Q)’
The truth table for the same is given below: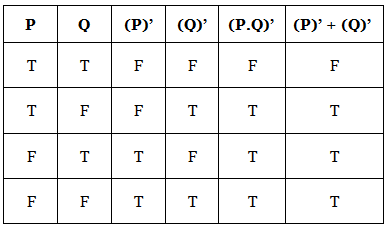
We can clearly see that truth values for (P.Q)’ are equal to truth values for (P)’ + (Q)’, corresponding to the same input. Thus, De Morgan’s First Law is true.
De Morgan’s Second laws
Statement: The Complement of the sum (OR) of two Boolean variables (or expressions) is equal to the product(AND) of the complement of each Boolean variable (or expression).
(P + Q)’ = (P)’.(Q)’
Proof:
The truth table for the same is given below: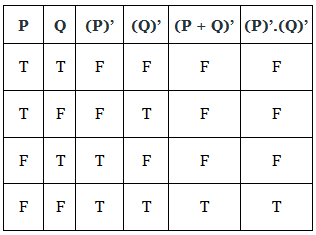
We can clearly see that truth values for (P + Q)’ are equal to truth values for (P)’.(Q)’, corresponding to the same input. Thus, De Morgan’s Second Law is true.
|
75 videos|188 docs|70 tests
|
FAQs on Boolean Algebra - Digital Circuits - Electronics and Communication Engineering (ECE)
| 1. What is Boolean algebra and how is it related to the GATE exam? |  |
| 2. What are the basic operations in Boolean algebra? |  |
| 3. How is Boolean algebra used in circuit simplification? |  |
| 4. What is the significance of Boolean algebra in digital logic design? |  |
| 5. Can Boolean algebra be used for solving real-world problems? |  |
















