Boundary-Layer Theory | Fluid Mechanics for Civil Engineering - Civil Engineering (CE) PDF Download

Introduction

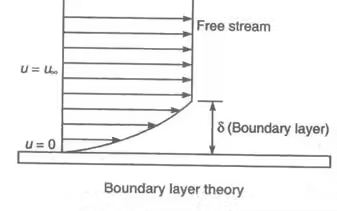
When a real fluid flows over a solid body, the velocity of the fluid at the boundary will be zero. If the boundary is stationary. As we move away from the boundary in perpendicular direction velocity increases to the free stream velocity. It means velocity gradient (du/dy) will exist.

Note: Velocity gradient du/dy does not exist outside the boundary layer as outside the boundary layer velocity is constant and equal to free stream velocity.

Development of Boundary Layer

Development of boundary layer can be divided into three regions: laminar, transition, turbulent.
Reynolds number

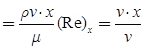
For the laminar boundary layer
(Re)x < 5 × 10⁵ (For flat plate) and if (Re)x > 5 × 10⁵
where Re = Reynolds's number
Then, flow is turbulent.

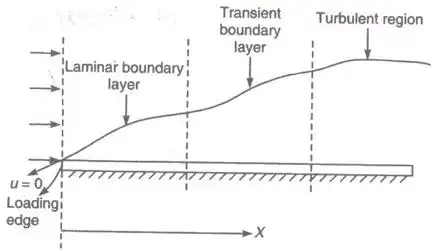
Here, x is the distance from the leading edge in the horizontal direction.

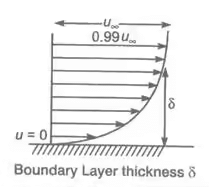
Boundary-Layer Thickness (δ) 

It is the distance from the boundary to the point where the velocity of the fluid is approximately equal to 99% of free stream velocity. It is represented by δ.

Displacement Thickness (δ*)

It is observed that inside the boundary layer velocity of the fluid is less than the free stream velocity hence, discharge is less in this region. To compensate for the reduction in discharge the boundary is displaced outward in a perpendicular direction by some distance. This distance is called displacement thickness (δ*).

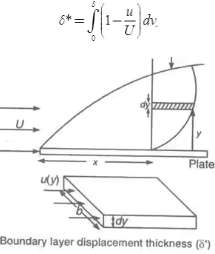
Momentum Thickness (θ) 

As due to boundary layer reduction in velocity occurs so, momentum also decreases. Momentum thickness is defined as the distance measured normal to the boundary of the solid body by which the boundary should be displaced to compensate for the reduction in the momentum of flowing fluid.

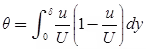
Energy Thickness (δ**)

It is defined as distance measured perpendicular to the boundary of a solid body by which the boundary should be displaced to compensate for the reduction in kinetic energy of flowing fluid (KE decreases due to formation of the boundary layer)

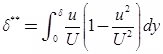
Boundary Conditions for the Velocity Profile 

Boundary conditions are as:
(a) At y = 0, u = 0, du / dy ≠ 0
(b) At y = δ, u = U, du / dy = 0

Laminar Flow

A flow in which fluid flows in layer and no intermixing with each other is known as laminar flow. For circular pipe, the flow will be laminar.

If Re = ρvD/μ < 2000
Where, ρ = Density of fluid, v = Velocity of fluid,
D = Diameter of pipe, μ = Viscosity of fluid.
For a flat plate, the flow will be laminar.
If Re = ρvL/μ < 5 x 10⁵
Where L is the length of the plate.

Turbulent Flow 

In this flow, an adjacent layer of fluid cross each other (particles of fluid move randomly instead of moving in a streamlined path), for flow inside the pipe. If Re > 4000, the flow is considered turbulent, for flat plate, Re > 5 × 10⁵.
Von Karman Momentum Integral Equation

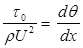
where, θ = momentum thickness
Shear stress: 

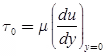
Where, U = Free stream velocity; ρ = Density of fluid.

It is defined as the ratio of the shear stress τ0 to the quantity1/2ρU²
It is denoted by 

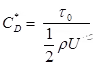
Average Coefficient of Drag (CD):

It is defined as the ratio of the total drag force to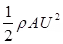

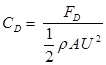
Where, A = Area of surface,
U = Free stream velocity, ρ = Mass density of the fluid.

Blasius Experiment Results

For laminar flow,

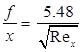
Coefficient of drag

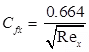
Average coefficient of drag

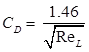
For turbulent flow,

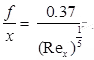
where x = Distance from leading-edge, Re_x = Reynolds's number for length x.
ReL = Reynolds's number at end of the plate
Coefficient of drag

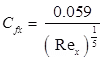
Average coefficient of drag

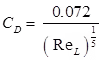
For laminar flow
f ∝ √x
f = Boundary layer thickness,

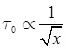
τ₀ = Shear stress at the solid surface
x = Distance from where solid surface starts.
Velocity profile for turbulent boundary layer is
u / U = (9y / f)^{1 / n} ⇒ 1 / n = 1 / τ
⇒ 5 x 10⁵ < Re < 107

Conditions for Boundary Layer Separation: Let us take curve surface ABCSD where fluid flow separation print S is determined from the condition (du/dy)_y = 0

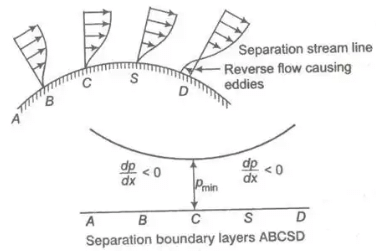
If (du / dy)_{y = 0} = -ve, 

the flow is separated (dp / dx > 0)  

If (du / dy)_{y = 0} = 0,

the flow is on the average of separation (∂ρ / ∂x = o)

If (∂u / ∂y) _{y = 0} = +ve the flow will not separate or flow will remain attained (dp / dx < 0) 

Methods of Preventing Separation of Boundary Layer

Suction of slow-moving fluid by a suction slot.

• Supplying additional energy from a blower.
• Providing a bypass in the slotted
• Rotating boundary in the direction of flow.
• Providing small divergence in a diffuser.
• Providing guide blades in a bend.
• Providing a tripwire ring in the laminar region for the flow over a sphere.