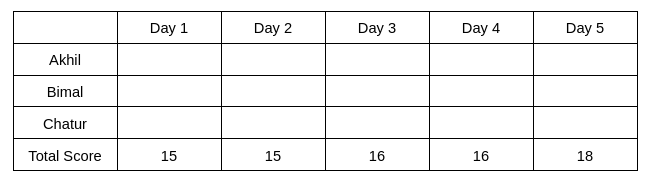
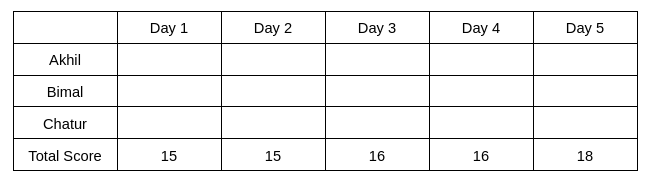
Let the total score of day 1, day 2, day 3, day 4, and day 5 are d1, d2, d3, d4, and d5, respectively.
The table shows that d1+d2 = 30 ... eq (1), d2+d3 = 31 ... eq (2), d3+d4 = 32 .... eq(3), d4+d5 = 34 ... eq(4)
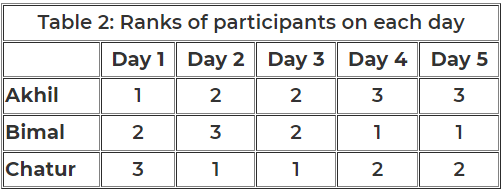
It is given that participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. All participants with a tied score are awarded the best available rank if there is a tie.
It is given that the total score on Day 3 is the same as the total score on Day 4.
Therefore, d3 = d4 => d3 = d4 = 16, which implies d2 = 15, d5 = 18, and d1 = 15.
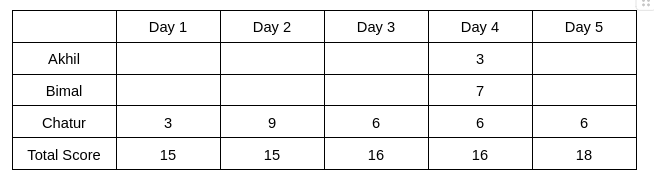
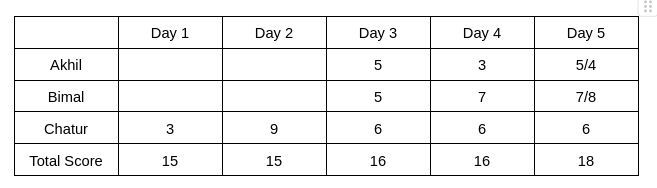
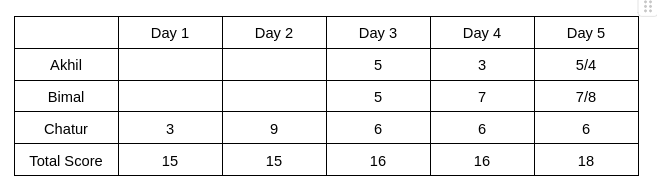
The day-wise score is given below:

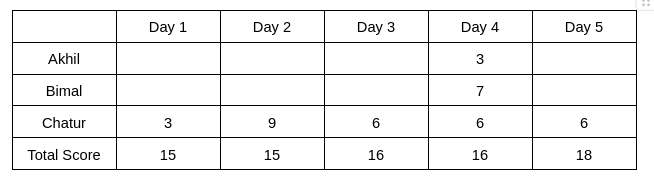
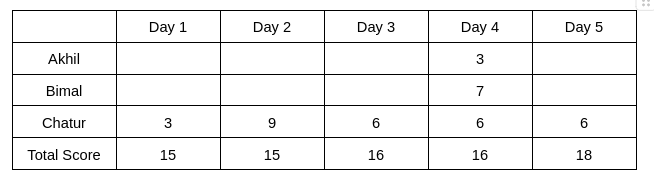
It is known that Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
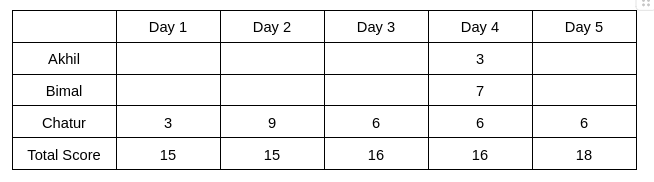
Hence, only Chatur scored 9 (one time) on Day 2, and no other person scored 9 on any of the given 5 days. Chatur scored 3 only one time, which was on Day 1. Therefore, the scores obtained by Chatur on Day 3, Day 4, and Day 5 are 6, 6, and 6, respectively. It is also known that Akhil's score on Day 4 is the same as the score obtained by Chatur on Day 1. Hence, Akhil's score on Day 4 is 3.
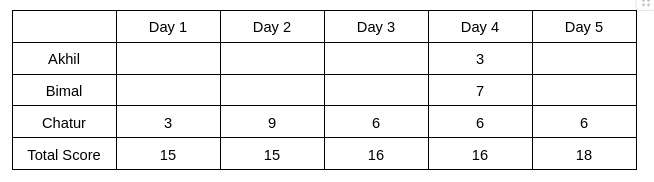
Hence, we get the following table:

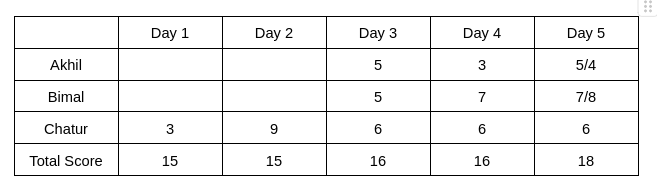
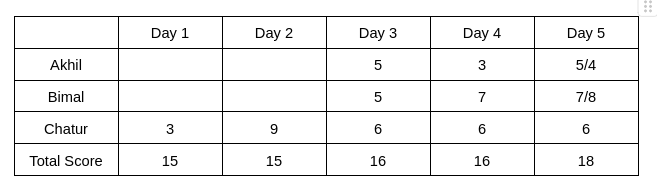
From Table 2, we see that the rank of Bimal and Akhil is the same, which is 2. Hence, The score obtained by Akhil and Bimal is the same. Let the score be x. Therefore, 6+2x = 16 => x = 5
The rank of Chatur on Day 5 is 2, and the rank of Bimal is 1, which implies the score obtained by Bimal will be more than Chatur. Hence, Bimal can score either 7 or 8 on Day 5. Therefore, the score obtained by Akhil on Day 5 is either 5 or 4.

It is given that Bimal’s scores are the same on Day 1 and Day 3. Hence, the score obtained by Bimal on Day 1 is 5, which implies The score obtained by Akhil is 7 on Day 1.
From Table 2, we can see that the rank of Bimal is 3 on Day 2, and the rank of Akhil is 2 on Day 2. Hence, the score of Bimal will be lower than Akhil on Day 2.
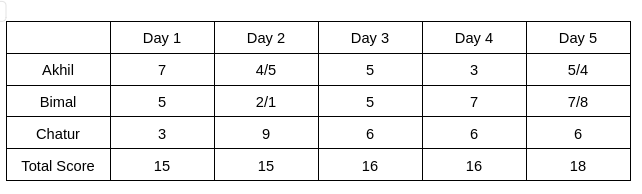
Let the score of Akhil be a, and the score of Bimal be b. Then 9+a+b = 15, and a > b
=> a+b =6, and a> b
Hence, the value of a can be 4/5, and the value of b can be 2/1
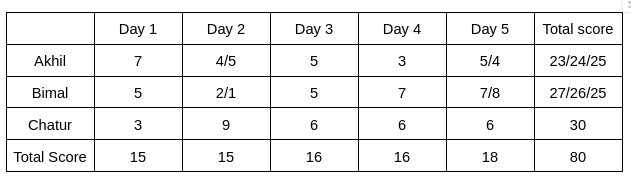
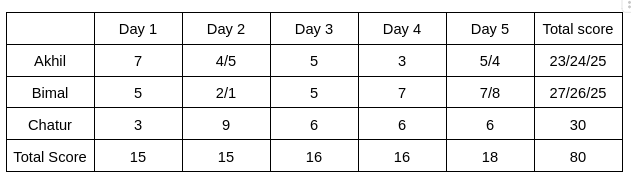
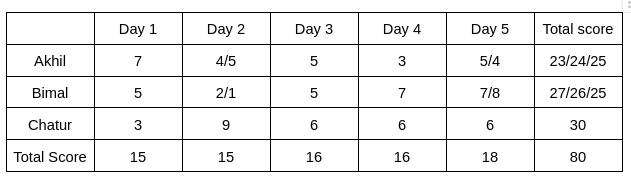
Therefore, the final table is given below:

In the question, it is given that the total score obtained by Bimal is a multiple of 3, which implies the total score obtained by Bimal is 27, which implies the total score obtained by Akhil is 23.
Akhil will score 23, when his scores on Days 1, 2, 3, 4, and 5 are 7, 4, 5, 3, 4, respectively.
Hence, the score obtained by him on Day 2 is 4.
The correct option is A

 The following information is also known.
The following information is also known.