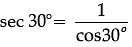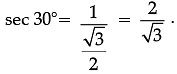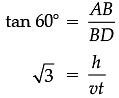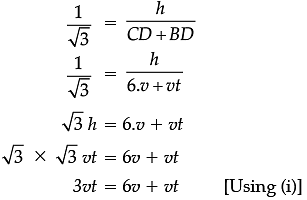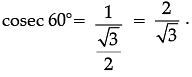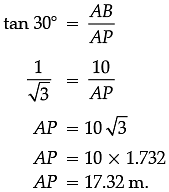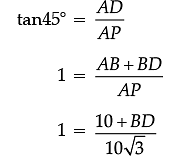Q1:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself:Read the following text and answer the following questions on the basis of the same.
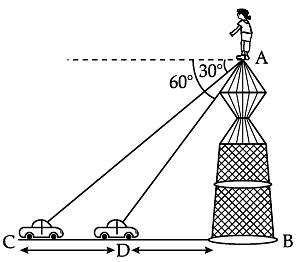
A straight highway leads to the foot of tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°.

Q. Write the value of sec 30°.
Explanation
Report a problem
Q2:
Question for Case Based Questions: Some Application of Trigonometry
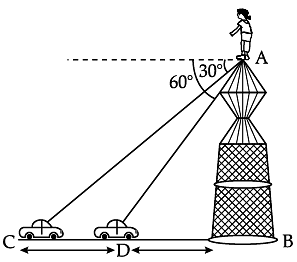
Try yourself: Read the following text and answer the following questions on the basis of the same.A straight highway leads to the foot of tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°.

Q. The line drawn from the eye of an observer to the point in the object viewed by the observer. Explanation
The line of sight is the line drawn from the eye of an observer to the point of the object viewed by the observer. The angle of elevation of an object viewed , is the angle formed by the line of sight with the horizontal when object viewed is above the horizontal level.
Report a problem
Q3:
Question for Case Based Questions: Some Application of Trigonometry
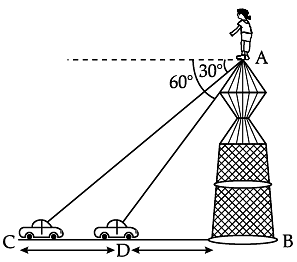
Try yourself: Read the following text and answer the following questions on the basis of the same.A straight highway leads to the foot of tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°.

Q. Find the time taken by the car to reach the foot of the tower from point D to B. Explanation
Let AB be the vertical tower of height h m.
Let the speed of car be v m/s.
Let car takes t seconds to reach the point B from the point D
Distance travel by car in t sec = vt m.
In ΔABD, we have

h = √3 vt ...(i)
and in right D ABC, we have


2vt = 6v

Report a problem
Q4:
Question for Case Based Questions: Some Application of Trigonometry
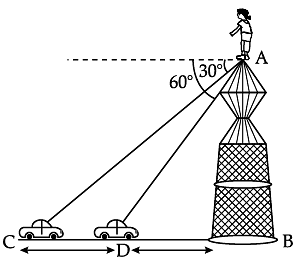
Try yourself: Read the following text and answer the following questions on the basis of the same.A straight highway leads to the foot of tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°.

Q. Write the value of cosec 60°.
Explanation
cosec 60°=


Report a problem
Q5:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of the same.A straight highway leads to the foot of tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°.

Q. If the two lines are parallel; then the alternate opposite angles are ..................... .
Explanation
Alternate angles are equal, corresponding angles are equal, co-interior angles are supplementary. Vertically opposite angles are equal. So, all of the options are correct.
Report a problem
Q6:
Question for Case Based Questions: Some Application of Trigonometry
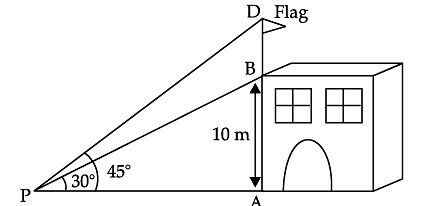
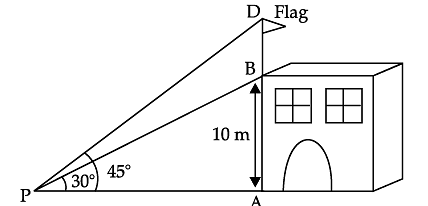
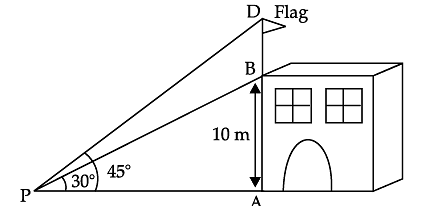
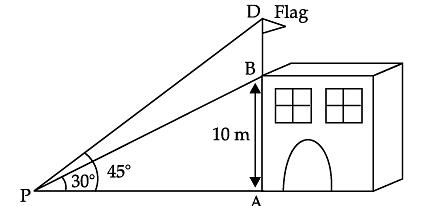
Try yourself: Read the following text and answer the following questions on the basis of the same.Form a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and angle of elevation of the top of the flagstaff from P is 45°.

Q. Find the distance of the building from the point P. Explanation
In right DPAB, we have

Report a problem
Q7:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of the same.Form a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and angle of elevation of the top of the flagstaff from P is 45°.

Q. What is the value of tan 45°?
Explanation
Value of tan 45° = 1.
Report a problem
Q8:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of the same.Form a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and angle of elevation of the top of the flagstaff from P is 45°.

Q. Find the length of flagstaff. Explanation
In right ΔPAB
tan 30° = 

AP = 10 √3 m
In right ΔPAD,

10 √3 = 10 + BD
BD = 10 √3 – 10
BD = 7.32 m.
Report a problem
Q9:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of the same.Form a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and angle of elevation of the top of the flagstaff from P is 45°.

Q. What is the value of tan 30°? Explanation
Value of tan 30° = 1/√3
Report a problem
Q10:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of the same.Form a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and angle of elevation of the top of the flagstaff from P is 45°.

Q. Write the Pythagoras theorem for DAPB. Explanation
Pythagoras theorem for DAPB is BP2 = AB2 + AP2.
Report a problem
Q11:
Question for Case Based Questions: Some Application of Trigonometry
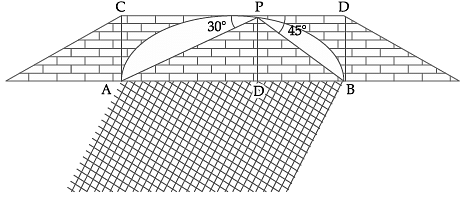
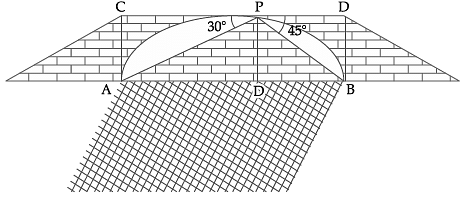
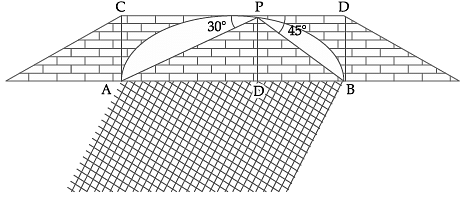
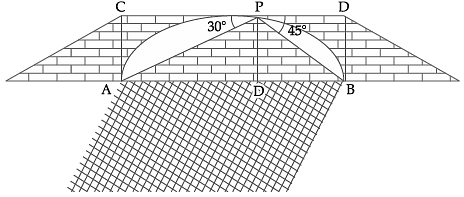
Try yourself: Read the following text and answer the following questions on the basis of same.From a point on the bridge across a river the angle of depression of the banks on opposite sides of the river 30° and 45° respectively.

Q. Name the ΔAPD, Explanation
ΔAPD is right angled triangle Q
∵ ∠D = 90°
Report a problem
Q12:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself:Read the following text and answer the following questions on the basis of same.
From a point on the bridge across a river the angle of depression of the banks on opposite sides of the river 30° and 45° respectively.

Q. The value of tan 45° is
Explanation
The value of tan 45° is = 1
Report a problem
Q13:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of same.From a point on the bridge across a river the angle of depression of the banks on opposite sides of the river 30° and 45° respectively.

Q. If the bridge is at a height of 3 m from the banks, find the width of the river. Explanation
In ΔPDA, ∠A = 30°


AD = 3√3m
In ΔPDB, ∠B = 45°
tan 45° = PD/DB

DB = 3m
width of the river = AB = AD + DB
= 3√3 + 3
= 3(√3 + 1)m.
Report a problem
Q14:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of same.From a point on the bridge across a river the angle of depression of the banks on opposite sides of the river 30° and 45° respectively.

Q. In ΔAPD, tan 30° is Explanation
In ΔAPD, tan 30° = Perpendicular/Base
= PD/AD
Report a problem
Q15:
Question for Case Based Questions: Some Application of Trigonometry
Try yourself: Read the following text and answer the following questions on the basis of same.From a point on the bridge across a river the angle of depression of the banks on opposite sides of the river 30° and 45° respectively.

Q. The value of tangent in right angle triangle is equal to Explanation
The value of tangent in right angle triangle is equal to Perpendicular/Base.
Report a problem