Cauchy-Riemann equations | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Cauchy-Riemann Equations |

|
| Cauchy-Riemann Equations in Polar Form |

|
| Cauchy-Riemann Equations and Their Applications |

|
| Solved Numericals |

|
Cauchy-Riemann Equations
The Cauchy-Riemann equations play a crucial role in examining differentiability and continuity. These equations are essential for the formation of various holomorphic complex functions in mathematics and are used to study analytic functions. The functions involved in the Cauchy-Riemann equations are real-valued and depend on two variables. The equations are expressed as:- f(x, y) l(x, y)
- df/dx = dv/dy
- df/dy = dv/dx
In these equations, the variables represent components of a complex-valued function, with both real and imaginary parts. The partial derivatives in these equations must satisfy the Cauchy-Riemann conditions. Holomorphic complex differentiable functions are characterized by these equations, making them valuable for solving partial differential equations. Due to their significance, the Cauchy-Riemann equations are frequently encountered in various competitive exams. The property of a complex function being holomorphic means it is differentiable and related to a specific subset of complex functions.
Cauchy-Riemann Equations in Polar Form
The Cauchy-Riemann equations in polar form are a variant of the standard Cauchy-Riemann equations, adapted to polar coordinates. These equations are part of the complex value function system in mathematics, dealing with both real and imaginary parts of the variables. They are especially useful in solving partial differential equations.Cauchy Riemann equations in polar form are expressed as: fu/fr = 1/r fv/fo and fv/fr = -1 /r fu/fo.
These equations can be transformed into the Cartesian form for complex functions, where the polar form represents complex numbers in a rectangular shape when plotted on a graph. This transformation is vital for understanding the behavior of holomorphic functions in different coordinate systems.
Summary: The Cauchy-Riemann equations in polar form provide a framework for examining complex functions using polar coordinates, allowing for the analysis of partial differential equations in a more versatile manner. This approach is essential for working with complex numbers and functions in various mathematical contexts.
Cauchy-Riemann Equations and Their Applications
The Cauchy-Riemann equations are fundamental in solving problems involving complex numbers and have applications across various mathematical fields. They are used to determine the values of partial derivatives, commonly denoted as u and v, which are the real and imaginary parts of a complex-valued function. These equations ensure that partial derivatives satisfy specific conditions, representing holomorphic, or complex-differentiable, functions.Applications of Cauchy-Riemann Equations
- Determining Partial Derivatives: The equations help in finding the partial derivatives of complex functions.
- Computing Derivatives: They are essential for computing the derivatives of complex functions.
- Holomorphic Functions: They characterize functions that are holomorphic, meaning they are differentiable in the complex plane.
Polar Form of Cauchy-Riemann Equations
The polar form of the Cauchy-Riemann equations is derived from the Cartesian form and is particularly useful when dealing with complex numbers in polar coordinates. The equations in polar form are: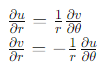
The polar form represents complex numbers in a rectangular shape when plotted on a graph and is also a conjugate function of harmony.
Conclusion
The Cauchy-Riemann equations are crucial in mathematics for analyzing and solving problems involving complex functions. They ensure the proper behavior of partial derivatives and are used in both Cartesian and polar forms. In polar coordinates, they are expressed as: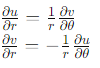 These equations play a vital role in ensuring the differentiability and continuity of complex functions.
These equations play a vital role in ensuring the differentiability and continuity of complex functions.Solved Numericals
Q1. The value of k that makes the complex-valued function 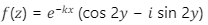 analytic, where z = x + iy, is _________.
analytic, where z = x + iy, is _________.
(Answer in integer)
Ans: 1.999 - 2.001
For a function f(z) = u + iv to be analytic, then u and v should obey Cauchy-Riemann equations.
C-R Equations: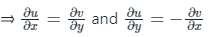
Given,
f(Z) = u(x, y) + iv(x, y)
f(Z) = e-kx cos 2y - ie-kx sin 2y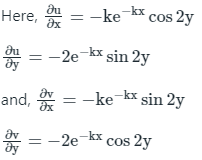
Since f(Z) is analytic, it will satisfy Cauchy-Riemann equation,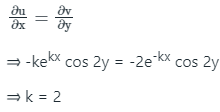
Q2. If 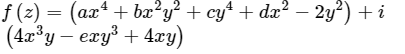 is analytic, then a, b, c, d, e are ______.
is analytic, then a, b, c, d, e are ______.
Solution: Given: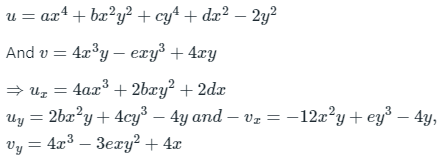
Now,
Consider ux = vy & uy = -vx (C-R equations)
⇒ a = 1, 2b = -3e, 2d = 4
& 2b = -12, 4c = e
∴ a = 1, b = - 6, c = 1, d = 2 & e = 4.
Q3. If f(z) = u + iv is an analytic function of z = x + iy and u – v = ex (cosy - siny), then f(z) in terms of z is
Solution:
f(z) = u + iv
⇒ i f(z) = - v + i u
⇒ (1 + i) f(z) = (u - v) + i(u + v)
⇒ F(z) = U + iv, where F(z) = (1 + i) f(z)
U = u – v, V = u + v
Now,
Let F(z) be an analytic function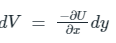
dV = ex (sin y + cos y) dx + ez(cosy – siny) dy
∴ dV = d[ex(siny + cosy)]
Now,
On integrating
V = ex (siny + cosy) + c1
F(z) = U + iV = ex(cosy - siny) + i ex (siny + cosy) + ic1
F = ex(cosy + isiny) + iex (cosy + isiny) + ic1
F(z) = (1 + i) ex + iy + ic1 = (1 + i)ez + ic1
⇒ (1 + i) F(z) = (1 + i) ez + ic1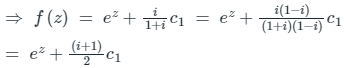
∴ f(z) = ez + (1 + i) c
Q4. An analytic function of a complex variable 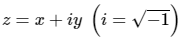 is defined as f(z) = x2- y2 + iψ (x, y), where ψ(x, y) is a real function. The value of the imaginary part of f(Z) at z = (1 + i) is _______ (round off to 2 decimal places).
is defined as f(z) = x2- y2 + iψ (x, y), where ψ(x, y) is a real function. The value of the imaginary part of f(Z) at z = (1 + i) is _______ (round off to 2 decimal places).
Ans: 1.99 - 2.01
Solution: f(z) = ϕ + iψ
ϕ = Real part, ψ = Imaginary part
If f(z) is analytic function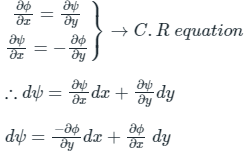
Calculation:
Given, f(z) = x2 – y2 + i ψ (x, y)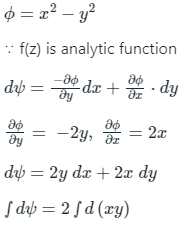
ψ = 2 xy
Given, z = 1 + i
Comparing it with z = x + iy, we get:
∴ x = 1, y = 1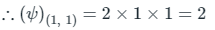
|
44 videos|109 docs|58 tests
|
FAQs on Cauchy-Riemann equations - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are the Cauchy-Riemann equations? |  |
| 2. How are the Cauchy-Riemann equations represented in polar form? |  |
| 3. What are some applications of the Cauchy-Riemann equations? |  |
| 4. How are the Cauchy-Riemann equations relevant to mechanical engineering? |  |
| 5. Are there any practical examples where the Cauchy-Riemann equations are used in mechanical engineering? |  |















