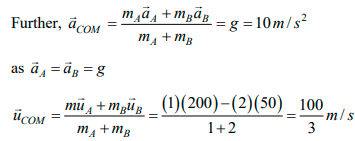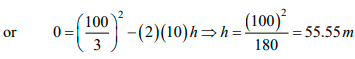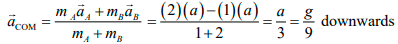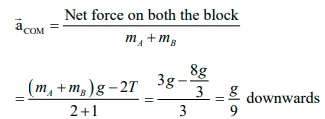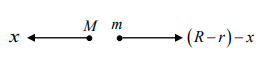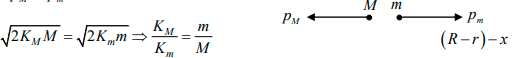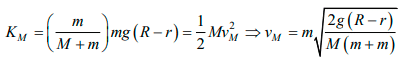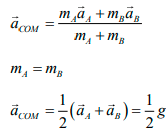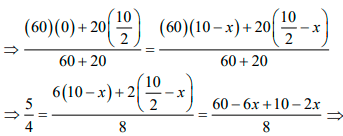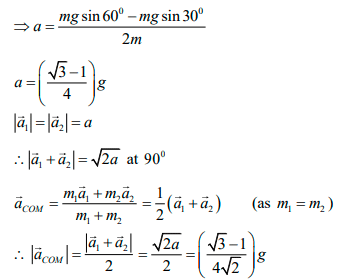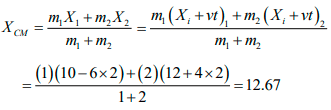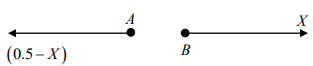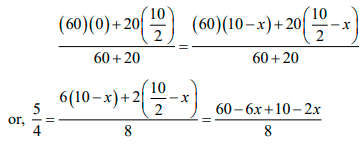Centre of Mass and its Applications: Assignment | Mechanics & General Properties of Matter - Physics PDF Download

Q.1. Two particles A and B of mass 1kg and 2kg respectively are projected in the direction shown in figure with speed u_{A =} 200m/s and u_B = 50m/s. Initially they where 90m apart. Find the maximum height attained by the center of mass of the particles. Assume acceleration due to gravity to be constant (g = 10m/s²)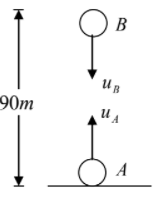

Using m_Ar_A  = m_Br_B ⇒ (1) (r_A) = 2(r_B) ⇒ r_A = 2r_B

And r_A + r_B = 90m

Solving these two equations, we get r_{A =} 60m and r_B =30m

i. e., COM is at the height 60m from the ground at time t = 0.

Let, h be height attained by COM beyond

60m. Using, v²_COM = u²_COM + 2a_COMh

Therefore, maximum height attained by the centre of mass is H = 60 + 55.55 = 115.55m

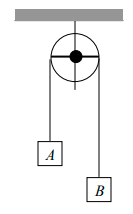
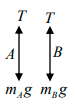
Q.2. In the arrangement shown in figure, m_A = 2kg and m_B = 1 kg. String is light and inextensible. Find the acceleration of centre of mass of both the blocks. Neglect everywhere.

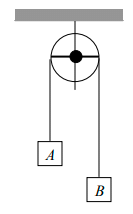
Net pulling force on the system is (m_A - m_B)g = (2 - 1)g = g

Total mass being pulled is m_A + m_B or 3kg

∴ a = Net pulling force / Total mass = g/3

Alternate method:

Free body diagram of block A is shown figure.

2g - T = m_A (a) ⇒ T = 2g - m_Aa = 2g - (2) (g/3)= 4g/3

Free body diagram of A and B both are shown in figure

Q.3. A block of mass M with a semicircular track of radius R rests on a horizontal frictionless surface shown in figure. A uniform cylinder of radius r and mass m is released from rest at the point A. The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom of the truck? How fast is the block moving when the cylinder reaches the bottom of the track?

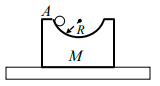
(i) Mx = m(R - r - x)

x = m(R - r)/M + m

(ii) P_{M  =}  P_m

_{KM + Km} decrease in potential energy of m = mg (R - r)
Solving these two equations we get, 

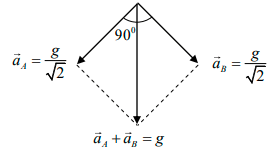
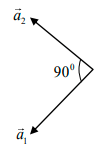
_{Q.4. Two blocks A and B of equal mass are released on two sides of a fixed wedge C as shown in figure. Find the acceleration of centre of mass of block A and B .Neglect friction.}

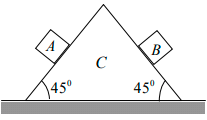
_{Acceleration of both the blocks will be g sin 45}⁰ _{or g/√2 at the right angle to each}

_{other, Now}

_{Q.5. A plank of mass 5kg is placed on a frictionless horizontal plane. Further a block of mass 1kg is placed over the plank. A massless spring of natural length 2m is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring’s natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is 100/N m)}

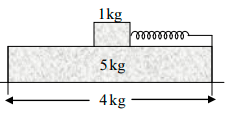
_{Let the velocity of the block and the plank, when the block leaves the spring be and v respectively.}

_{By conservation of energy 1/2 kx}² _{= 1/2mu}² _{+ 1/2Mv}² _{[M = mass of the plank m = mass of the block]}

_{⇒   100 = u}² _{+ 5V}²

_{By conservation of momentum mu + Mv = 0}

_{u = -5v}

_{Solving equation (i) and (ii)}

_30v² _{= 100 ⇒ v = √10/3 m / s}

_{From this moment until block falls, both plank and block keep their velocity constant.}

_{Thus, when block falls, velocity of plank √10/2 m/s.}

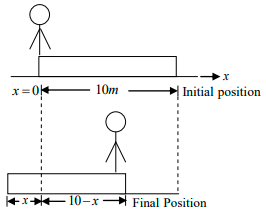
Q.6. A wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m . Find the displacement of the plank over the floor when the man reaches the other end of plank.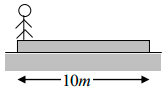

Here, the system is man + plank. Net force on this system in horizontal direction is zero and initially the centre of mass of the system is at rest. Therefore, the centre of mass does not move in horizontal direction.
Let x be the displacement of the plank. Assuming the origin, i. e., x = 0 at the position shown in figure.

 

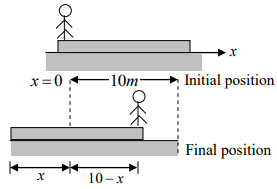
As we said earlier also, the centre of mass will not move in horizontal direction

(x - axis).Therefore, for centre of mass to remain stationary,

x_i = x_f

_{⇒ 5 = 30 - 3x + 5 - x}

_{⇒ 4x = 30 ⇒ x = 30 / 4m ⇒  x = 7.5m}

_{Note: The centre of mass of the plank lies at its centre.}

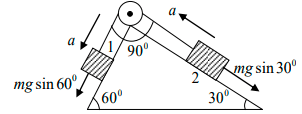
_{Q.7. Two blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of the centre of mass of the two blocks when they are released from rest. Neglect friction}

_{a = Net pulling force / Total mass}

     

              

_{Q.8. A block of mass 1kg is at x =10m and moving towards negative x -axis with velocity 6m/s. Another block of mass 2kg is at x = 12m and moving towards positive x -axis with velocity 4m / s at the same instant. Find position of their centre of mass after 2s.}

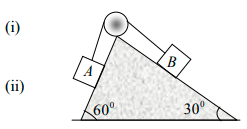
_{Q.9. Block A has a mass of 5kg and is placed on top of a smooth triangular block, B having mass of 30kg . If the system is released from rest, determine the distance, B moves when A reaches the bottom. Neglect the size of block A .}

 

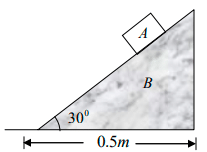
m_Ax_A = m_BX_B

∴ (5)(0.5-x) = 30

∴ x = 0.0714m = 71.4mm

_{Q.10. A wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m . Find the displacement of the plank over the floor when the man reaches the other end of the plank.}

Here, the system is man + plank. Net force on this system in horizontal direction is zero and initially the centre of mass of the system is at rest. Therefore, the centre of mass does not move in horizontal direction.
Let x be the displacement of the Plank. Assuming the origin, i.e., x = 0 at the position shown in figure.

As we said earlier also, the centre of mass will not move in horizontal direction ( x -axis). Therefore, for centre of mass to remain stationary.

⇒ x_i = x_f

Where x_i and x_f denote the initial and final position of centre of mass.

or, 5 = 30 - 3x + 5 - x

or, 4x = 30 ⇒ x = 30/4 m = 7.5m

Note: The centre of mass of the plank lies at its centre.