All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Notes  >  Thermodynamics  >  Basics & Air Standard Cycles

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering PDF Download

Overview

  • A heat engine is a device which transforms the chemical energy of a fuel into thermal energy and uses this energy to produce mechanical work.

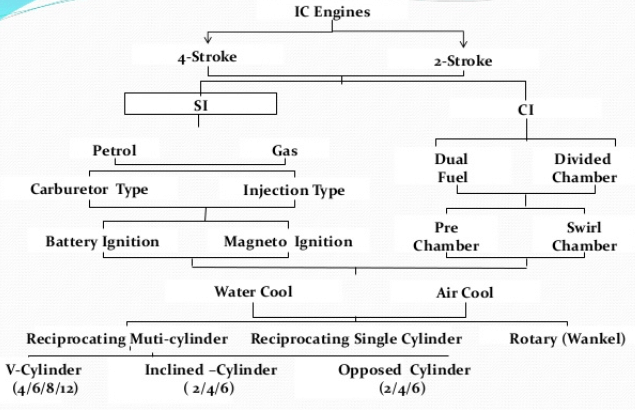
Materials for Construction of I.C Engine parts
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Components of IC Engine

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Various Strokes of 4-stroke Engine 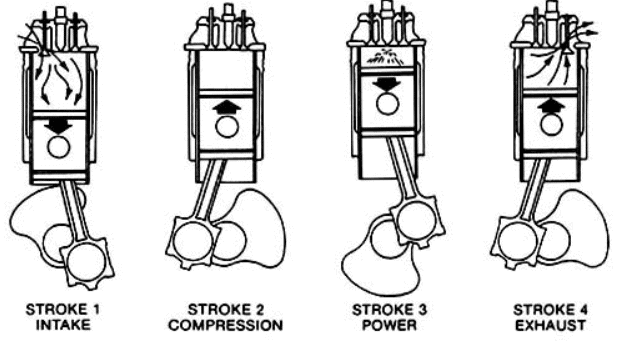Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering                   Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering                     

Two Stroke Engines

  • In two stroke engine, two strokes of piston or one revolution of crankshaft completes the cycle.
  • Inlet of mixture or fuel and exhaust of combustion products starts one by one (first exhaust port is opened then inlet port) in the expansion stroke and completes one by one (first inlet port is closed then exhaust port) in compression stroke. The piston head has deflector to avoid exhaust of fresh mixture from exhaust port.

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering


Question for Basics & Air Standard Cycles
Try yourself:
What is the purpose of a heat engine?
View Solution

Scavenging process

  • The process of cleaning the cylinder after the expansion stroke is scavenging. Here the fresh fuel or mixture pushes the exhaust to exhaust port.

Type of scavenging process

  • Uniflow system has highest scavenging efficiency

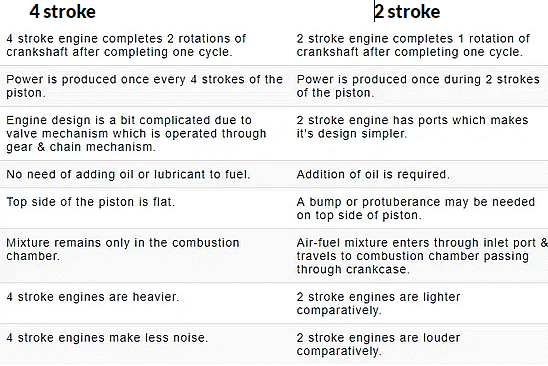
Basics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringBasics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringBasics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Comparison of four stroke and two-stroke engine 

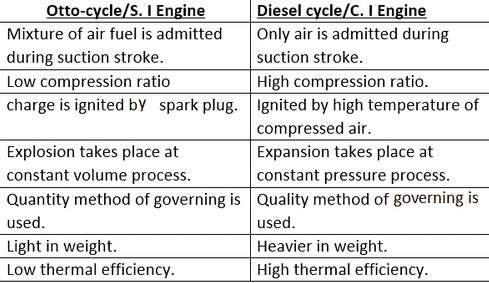
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Comparison of engines working on Otto and Diesel Cycle

Basics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringNote: High speed diesel engine follows dual cycle.

Performance Parameters of I.C. Engine

  • The energy of the fuel that is converted to power is called the indicated power (i.p.)
  • The energy of the fuel that is converted to passes through the connecting rod to the crank shaft. In this transmission there are energy losses, due to friction, pumping etc. The sum of all there losses converted to power is termed as friction power (f.p)
  • Brake power (b.p.) = Indicated power (i.p.) – Friction power (f.p.)
  • Indicated Thermal Efficiency (hit )

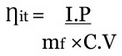
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

where,  
mf = mass of fuel /sec
QLHV = Lower calorific value of fuel
I.P. = Indicated power

  •  Brake thermal efficiency (hb.t )

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • Mechanical efficiency (hm)

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • Volumetric efficiency (ηV)

Volume of air actually inducted
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • Brake Specific Fuel Consumption (bsfc)

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
mf = mass of fuel/hour (kg/h)
B.P. = brake power (kW)

  • Indicated Specific fuel consumption (isfc)

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  •  Air fuel ratio (A/F ratio)

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  •  Stoichiometric Air fuel ratio

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • Heating value : when the product of combustion are cooled to 25ºC, practically all the water resulting from the combustion process will be condensed. The heating value so obtained is higher heating value. When water vapour are not condensed then the heating value is lower calorific value.
  • Lower calorific value of fule (QLHV)

QLHV = QHHV - mw ´ LW
QHHV = Higher calorific value
mW = mass of water vapour
Lw = Latent heat of Condensation of water vapour

  • i.p = Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
       (for two stroke engine)
  •  i.p =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
    (for four stroke engine)
  • b.p =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

P = π

L = Stroke of the piston
A = Cross sectional area of the cylinder
N = r.p.m. of the crank shaft
n = number of cylinders
T = Torque on the crank shaft

Mean Effective Pressure
Pmean (V1 – V2) = Workdone
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
Pm(mean effective pressure) is the constant hypothetical pressure acting during the cycle which produces the same work output as the actual cycle. Increasing the compression ratio will increase the Pmean which increases the efficiency of the cycle.

Assumption of Ideal Air Standard Cycle

  • The working medium is assumed to be a perfect gas and follows the relation PV = mRT.
  • There is no change in the mass of the working medium.
  • All the processes in the cycle are assumed to be reversible.
  • There is no heat loss from the system to the surroundings.
  • The working medium has constant specific heats throughout the cycle.
  • Physical constant Cp, Cv, g and m of the working medium are the same as those of air at standard atmospheric conditions

Question for Basics & Air Standard Cycles
Try yourself:
Which process involves pushing the exhaust out of the cylinder in an engine?
View Solution

Otto Cycle 

  • It is a reversible cycle

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Process Description
Compression1-2adiabatic
Combustion 2-3isobaric
Expansion3-4Adiabatic
Exhaust 4-1Isochoric
  • Compression ratio (r) =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
  •  Thermal efficiency(hth) =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
  • As the compression ratio r increases, efficiency increases. Limit of compression ratio is subject to knocking phenomenon in SI engine.

Diesel Cycle

  • It is also a reversible cycle

  Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
  Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

ProcessDescription
Compression1-2adiabatic
Combustion 2-3isochoric
Expansion3-4Adiabatic
Exhaust 4-1Isochoric

 

  • Compression ratio (r) =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
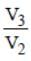
  •  Cut off ratio(rc) = Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering     
  • Expansion ratio (re)Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

rc * re = r

  • Thermal efficiency(ηdiesel)

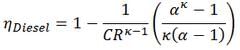
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • ηDiesel is the maximum thermal efficiency of a Diesel cycle
  • α is the cut-off ratio V3/V2 (i.e. the ratio of volumes at the end and start of the combustion phase)
  • CR is the compression ratio
  • κ = cp/cv = 1.4
  • As the compression ratio increase or cut- off ratio (rc) decreases, thermal efficiency hth of the diesel cycle increases

Dual Cycle

  • Dual cycle is the combination of both diesel cycle and otto cycle. The efficiency of dual cycle is more than diesel cycle but less than otto cycle. In heat addition process first there will be constant volume for some time and then constant pressure till the end of heat addition process. 
  • Process 1-2: Isentropic compression
  • Process 2-3: Addition of heat at constant volume.
  • Process 3-4: Addition of heat at constant pressure.
  • Process 4-5: Isentropic expansion.
  • Process 5-1: Rejection of heat at constant volume.
  • Compression ratio (r) =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
  • Pressure ratio (rp) =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
  • rc = V4/V3
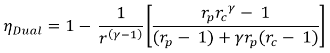
  •  Thermal efficiency =Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
  • When compression ratio increases or cut- off ratio 'r' decreases or pressure ratio
    (rp) increases efficiency 'ηdual' of the dual cycle increases.

(a) If r =1, Dual cycle becomes Otto cycle
(b) If rp =1, Dual cycle becomes Diesel cycle

Comparison Among Otto, Diesel & Dual Cycles

The important variable factors which are used as the basis for comparison of the cycle are compression ratio, peak pressure, heat addition, heat rejection and the net work. In order to compare the performance of the Otto. Diesel and Dual combustion cycles. some of the variable factors must be fixed. In this section, a comparison of these three cycles is made for the same comparison ratio, same heat addition, constant maximum pressure and temperature, same heat rejection and net work output. This analysis will show which cycles is more efficient for a given set of operating conditions.

Case-1 Same Compression Ratio and Heat Addition 

  • The Otto cycle 1-2-3-4-1, the Diesel cycle 1-2-3'-4'-1 and the Dual cycle 1-2- 2"3"4'-1 are shown in p-V and T-S diagram in figure (a) and (b) respectively for the same compression ratio and heat input.

Basics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringBasics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringFrom the T-S diagram, it can be seen that Area 5-2-3-6=Area 5-2-3'-6' = Area 5-2-2"-6" as this area represents the heat input which is the same for all cycles. All the cycles start from the same initial state point 1 and the air is compressed from state 1 to 2 as the compression ratio is same. It is seen from the T-S diagram for the same heat input, the heat rejection in Otto cycle (are 5-1-4-6) is minimum and
heat rejection in Diesel cycle (5-1-4'-6') is maximum. Consequently, Otto cycle has the least efficiency and Dual cycle having the efficiency between the two. One more observation can be made i.e., Otto cycle allows the working medium to expand more whereas Diesel cycle is least in this respect. The reason is heat is added before expansion in the case of Otto cycle and the last portion of heat
supplied to the fluid has a relatively short expansion in case of the Diesel cycle.
Case -2: Same Compression Ratio and Heat Rejection
Basics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringBasics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • Efficiency of Otto cycle is given by fig. (a) and (b)

hOtto =1- Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
where, Qs is the heat supplied in the Otto cycle and is equal to the area under the curve 2-3 on the T-s diagram. The efficiency of the Diesel cycle is given by
hDiesel =1-Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
where Q's is heat supplied in the Diesel cycle and is equal to the area under the curve 2-3' on the T=s Diagram. From the T-s diagram in fig.. it is clear that Qs> Q's i.e., heat supplied in the Otto cycle is more than that of the Diesel cycle.
Hence, it is evident that, the efficiency of the Otto cycle is greater than the efficiency of the Diesel cycle for a given compression ratio and heat rejection.
Case-3: Same Peak Pressure, Peak Temperature and Heat Rejection

  •  Figure (a) and (b) show the Otto cycle 1-2-3-4 and Diesel cycle 1-2'-3-4 on P-.V and T-s coordinates, where the peak pressure and temperature and the amount of heat rejected are the same.
    The efficiency of the Otto cycle.
    hOtto = 1- Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
    where, Qs in the area under the curve 2-3 in fig.(b.) The efficiency of the Diesel cycle, 1-2-2'-3-4 is,
    hDiesel = 1- Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Basics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringBasics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  • It is evident from fig. that Qs > Q's, Therefore, the Diesel cycle efficiency is greater than the Otto cycle efficiency when both engines are built to with stand the same thermal and mechanical stresses.

Case-4: Same maximum Pressure and Heat Input

Basics & Air Standard Cycles | Thermodynamics - Mechanical EngineeringBasics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

  •  For same maximum pressure and heat input, the Otto cycle (1-2-3-4-1) and Diesel cycle (1-2' -3' -4'-1) are shown on p-V and T-s diagrams in fig. (a) and (b) respectively. It is evident from the figure that the heat rejection for Otto cycle (area 1-5-6-4 on T-s diagram) is more than the heat rejected in Diesel cycle (1-5-6' - 4'). Hence Diesel cycle is more efficient than Otto cycle for the condition of same maximum pressure and heat input. One can make a note that with these conditions, the Diesel cycle has higher compression ratio than that of Otto cycle. One should also note that the cycle which is having higher efficiency allows maximum expansion.
    The Dual cycle efficiency will be between these two.

Case- 5: Same Maximum Pressure and work Output. 
The efficiency, h can be written as
Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
Refer to T-s diagram in previous fig. (b). For same work output the area 1-2-3-4 (Work output of Otto cycle) and area 1-2' -3' -4' (Work output of Diesel cycle) are same. To achieve this, the entropy at 3 should be greater than entropy at 3'. It is clear that the heat rejection for Otto cycle is more than that of Diesel cycle.
Hence , for these conditions, the Diesel cycle is more efficient than the Otto cycle.
The efficiency of Dual cycle lies between the two cycles.

  •  So for all the cases except when same compression ratio,

hDiesel >hDual >hOtto
hJoule <hOtto

  • In actual cycle, the assumption for air-standard cycle do not hold true for all the points. So efficiency of actual cycle is lower than air standard efficiency. The loss in efficiency of air standard cycle is due to the following reasons:
    • Loss due to variation of specific heat with temperature: As the temperature increases, specific heats (CP, CV) both increases but,

γ = Cp/Cv decreases so efficiency decreases.

  • Loss due to dissociation: At high temperature, the combustion products dissociate by absorbing some energy thereby reducing the efficiency.
  • Time loss: Fuel does not combust instantaneously and completely but takes some time to burn so the maximum pressure is reduced and efficiency decreases so spark is advanced to reduce time loss.
  • Exhaust blow down loss: Exhaust value is opened during expansion stroke to reduce work done by piston for exhaust stroke.
  • Pumping loss: The difference of work done in expelling the exhaust gases and the work done by fresh charge during suction is known as pumping loss.
  • Losses occur due to friction in moving parts of the engine.

Solved Numerical

Question:  A four-stroke single-cylinder SI engine of 6 cm diameter and 10 cm stroke running at 4000 r.p.m develops at a mean effective pressure of 10 bar. The power developed by the engine is

Solution: Mean Effective pressure: Imaginary pressure which remains constant, will give us the same work done like that of the actual cycle for the same volume as that of actual cycle.

Mean Effective Pressure = work done/swept volume

Swept volume of cylinder = 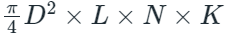Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

Where D is the diameter of the cylinder and L is the stroke of cylinder N is r.p.m and K is the number of cylinders.

For a 4-stroke engine since the two revolution of crank complete one cycle, therefore, there will be only suction stroke, then effective r.p.m N = N/2

Given: D = 6 cm = 6/100 m, L = 10 cm = 10/100 m, N = 4000 r.p.m, and Mean Effective Pressure = 10 bar = 10 x 100kPa

Pm = 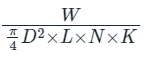Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

= 10 x 100 = 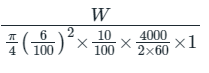Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

W = 9.42 kW

Question: The engine of a Lexus car has three cylinders with a total displacement of 770 cc. If the compression ratio is 8:7, then each cylinder has a clearance volume of

Solution: Compression Ratio (r) = 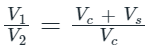 Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

(Vc and Vs are clearance and swept volume of single cylinder only.)

Total displacement volume = 770 cc, Compression ratio (r) = 8.7, Number of Cylinders = 3

Displacement or swept volume of one cylinder = Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

...  Swept volume (one cylinder) = 770/3 = 256.66 cc

Compression ratio (r) = 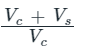Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

8.7 = (Vc + 256.66)/Vc 

... Vc = 32.246 cc

The document Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering is a part of the Mechanical Engineering Course Thermodynamics.
All you need of Mechanical Engineering at this link: Mechanical Engineering
29 videos|65 docs|36 tests
Join Course for Free

Top Courses for Mechanical Engineering

FAQs on Basics & Air Standard Cycles - Thermodynamics - Mechanical Engineering

1. What are the main components of an internal combustion engine?
Ans. The main components of an internal combustion engine include the cylinder, piston, connecting rod, crankshaft, valves, spark plug (in gasoline engines), fuel injector (in diesel engines), and the engine block.
2. How do two-stroke engines differ from four-stroke engines?
Ans. Two-stroke engines complete the combustion cycle in just two strokes of the piston (one upstroke and one downstroke), while four-stroke engines complete the cycle in four strokes (two upstrokes and two downstrokes). Two-stroke engines are generally simpler and lighter, but they tend to be less fuel-efficient and produce more emissions.
3. What are some performance parameters that are used to evaluate IC engines?
Ans. Performance parameters of IC engines include power output, torque, specific fuel consumption, thermal efficiency, volumetric efficiency, and emissions (such as carbon monoxide, nitrogen oxides, and hydrocarbons).
4. What is the assumption of an ideal air standard cycle?
Ans. The assumption of an ideal air standard cycle is that the working fluid is an ideal gas that follows the perfect gas law, and that all processes are internally reversible and adiabatic. It also assumes constant specific heats and neglects any heat transfer and frictional losses.
5. How do the Otto, Diesel, and Dual cycles differ from each other?
Ans. The Otto cycle is used in gasoline engines and assumes a constant volume heat addition process. The Diesel cycle is used in diesel engines and assumes a constant pressure heat addition process. The Dual cycle combines elements of both the Otto and Diesel cycles and assumes a combination of constant volume and constant pressure heat addition processes.
Related Exams
About this Document
11.5K Views
4.81/5 Rating
Nov 15, 2024 Last updated
Document Description: Basics & Air Standard Cycles for Mechanical Engineering 2024 is part of Thermodynamics preparation. The notes and questions for Basics & Air Standard Cycles have been prepared according to the Mechanical Engineering exam syllabus. Information about Basics & Air Standard Cycles covers topics like Overview, Components of IC Engine, Two Stroke Engines, Comparison of four stroke and two-stroke engine&nbsp;, Performance Parameters of I.C. Engine, Assumption of Ideal Air Standard Cycle, Comparison Among Otto, Diesel &amp; Dual Cycles and Basics & Air Standard Cycles Example, for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Basics & Air Standard Cycles.
Introduction of Basics & Air Standard Cycles in English is available as part of our Thermodynamics for Mechanical Engineering & Basics & Air Standard Cycles in Hindi for Thermodynamics course. Download more important topics related with notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Mechanical Engineering: Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering
Description
Full syllabus notes, lecture & questions for Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering - Mechanical Engineering | Plus excerises question with solution to help you revise complete syllabus for Thermodynamics | Best notes, free PDF download
Information about Basics & Air Standard Cycles
In this doc you can find the meaning of Basics & Air Standard Cycles defined & explained in the simplest way possible. Besides explaining types of Basics & Air Standard Cycles theory, EduRev gives you an ample number of questions to practice Basics & Air Standard Cycles tests, examples and also practice Mechanical Engineering tests
29 videos|65 docs|36 tests
Join Course for Free
Download as PDF
Explore Courses for Mechanical Engineering exam

Top Courses for Mechanical Engineering

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

,

study material

,

Viva Questions

,

ppt

,

Free

,

mock tests for examination

,

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

,

Objective type Questions

,

Previous Year Questions with Solutions

,

Summary

,

Important questions

,

past year papers

,

MCQs

,

pdf

,

Sample Paper

,

Extra Questions

,

Basics & Air Standard Cycles | Thermodynamics - Mechanical Engineering

,

practice quizzes

,

video lectures

,

Semester Notes

,

Exam

,

shortcuts and tricks

;
Additional Information about Basics & Air Standard Cycles for Mechanical Engineering Preparation

Basics & Air Standard Cycles Free PDF Download

The Basics & Air Standard Cycles is an invaluable resource that delves deep into the core of the Mechanical Engineering exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Basics & Air Standard Cycles now and kickstart your journey towards success in the Mechanical Engineering exam.

Importance of Basics & Air Standard Cycles

The importance of Basics & Air Standard Cycles cannot be overstated, especially for Mechanical Engineering aspirants. This document holds the key to success in the Mechanical Engineering exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Basics & Air Standard Cycles Notes

Basics & Air Standard Cycles Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Basics & Air Standard Cycles. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Basics & Air Standard Cycles Notes on EduRev are your ultimate resource for success.

Basics & Air Standard Cycles Mechanical Engineering Questions

The "Basics & Air Standard Cycles Mechanical Engineering Questions" guide is a valuable resource for all aspiring students preparing for the Mechanical Engineering exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Basics & Air Standard Cycles on the App

Students of Mechanical Engineering can study Basics & Air Standard Cycles alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Basics & Air Standard Cycles, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Basics & Air Standard Cycles is prepared as per the latest Mechanical Engineering syllabus.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup