Chapter 1 - Real Numbers, RD Sharma Solutions - (Part - 7) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 1.40
Q.14. Find the least number that is divisible by all the numbers between 1 and 10 (both inclusive).
Ans. TO FIND: Least number that is divisible by all the numbers between 1 and 10 (both inclusive)
Let us first find the L.C.M of all the numbers between 1 and 10 (both inclusive)
1 = 1
2 = 2
3 = 3
4 = 22
5 = 5
6 = 2 × 3
7 = 7
8 = 23
9 = 32
10 = 2 × 5
L.C.M = 2520
Hence 2520 is the least number that is divisible by all the numbers between 1 and 10 (both inclusive).
Q.15. A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60 and 72 km a day, round the field. When will they meet again?
Ans. GIVEN: A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60, and 72 km a day, round the field.
TO FIND: When they meet again.
In order to calculate the time when they meet, we first find out the time taken by each cyclist in covering the distance.
Number of days 1st cyclist took to cover 360 km = Total distance/Distance covered in 1 day = 360/48 = 7.5 = 75/10 = 15/2 days
Similarly, number of days taken by 2nd cyclist to cover same distance = 360/60 = 6 days
Also, number of days taken by 3rd cyclist to cover this distance = 360/72 = 5 days
Now, L.C.M of (15/2, 6 and 5) = L.C.M of numerators/H.C.F of denominators = 30/1 = 30 days
Thus, all of them will take 30 days to meet again.
Q.16. In a morning walk three persons step off together, their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that he can cover the distance in complete steps?
Ans. GIVEN: In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm and 90 cm.
TO FIND: minimum distance each should walk so that all can cover the same distance in complete steps.
The distance covered by each of them is required to be same as well as minimum. The required distance each should walk would be the L.C.M of the measures of their steps i.e. 80 cm, 85 cm, and 90 cm,
So we have to find the L.C.M of 80 cm, 85 cm, and 90 cm.
80 = 24 x 5
85 = 17 x 5
90 = 2 x 32 x 5
L.C.M of 80, 85, and 90 = 24 x 32 x 5 x 17
= 12240 cm
Hence minimum 12240 cm distance each should walk so that all can cove the same distance in complete steps.
Q.17. On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Ans. It is given that, three persons step out together and their steps measure 30 cm, 36 cm and 40 cm respectively.
The minimum distance each should walk so that each can cover the same distance in complete steps is the LCM of 30, 36 and 40.
30 = 2 × 3 × 5
36 = 2 × 2 × 3 × 3
40 = 2 × 2 × 2 × 5
Therefore, LCM of 30, 36 and 40 is 2 × 2 × 2 × 3 × 3 × 5 = 360
Hence, the minimum distance each should walk so that each can cover the same distance in complete steps is 360 cm.
Q.18. Find the largest number which on dividing 1251, 9377 and 15628 leaves remainders 1, 2 and 3 respectively.
Ans. On subtracting 1, 2 and 3 from 1251, 9377 and 15628 respectively, we get 1250, 9375 and 15625.
Now, we find the H.C.F of 1250 and 9375 by using Euclid's division lemma
9375 = 1250 × 7 + 625
∵ Remainder is not zero,
∴ we divide 1250 by 625 by using Euclid's division lemma
1250 = 625 × 2 + 0
Since, remainder is zero,
Therefore, H.C.F of 1250 and 9375 is 625.
Now, we find the H.C.F of 15625 and 625 by using Euclid's division lemma
15625 = 625 × 25 + 0
Since, remainder is zero,
Therefore, H.C.F of 15625 and 625 is 625.
Thus, H.C.F of 1250, 9375 and 15625 is 625.
Hence, the largest number which on dividing 1251, 9377 and 15628 leaves remainders 1, 2 and 3 respectively is 625.
Page No 1.49
Q.1. Show that the following numbers are irrational.
(i) 1/√2
Ans. Let us assume that 1/√2 is rational .Then , there exist positive co primes a and b such that
1/√2 = a/b
1/√2 = (a/b)2
⇒ 1/2 = a2/b2
⇒ b2 = 2a2
⇒ 2/b2 (∵2/2a2)
⇒ 2/b
⇒ b = 2c for some positive integer c
⇒ 2a2 = b2
⇒ 2a2 = 4c2 (∵ a = pc)
⇒ a2 = 2c2
⇒ 2/a2 (∵2/2c2)
⇒ 2/a
⇒ 2/a and 2/b
This contradicts the fact that a and b are co primes.
Hence 1/√2 is irrational
(ii) 7√5
Ans. Let us assume that 7√5 is rational .Then , there exist positive co primes a and b such that
7√5 = a/b
√5 = a/7b
We know that √5 is an irrational number
Here we see that √5 is a rational number which is a contradiction
Hence 7√5 is irrational.
(iii) 6 + √2
Ans. Let us assume that 6 + √2 is rational. Then , there exist positive co primes a and b such that
6 + √2 = a / b
Here we see that √2 is a rational number which is a contradiction as we know that √2 is an irrational number
Hence 6 + √2 is irrational.
(iv) 3 - √5
Ans. Let us assume that 3 - √5 is rational .Then, there exist positive co primes a and b such that
3 - √5 = a / b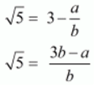
Here we see that √5 is a rational number which is a contradiction as we know that √5 is an irrational number
Hence 3 - √5 is irrational.
Q.2. Prove that following numbers are irrationals:
(i) 2/√7
Ans. Let us assume that 2/√7 is rational .Then , there exist positive co primes a and b such that
2/√7 = a/b
√7 = 2b/a
√7 is rational number which is a contradication.
Hence 2 / √7 is irrational.
(ii) 3/2√5
Ans. Let us assume that 3/2√5 is rational .Then, there exist positive co primes a and b such that
3/2√5 = a/b
√5 = 3b/2a
√5 is rational number which is a contradication.
Hence 3/2√5 is irrational.
(iii) 4 + √2
Ans. Let us assume that 4 + √2 is rational .Then , there exist positive co primes a and b such that
4 + √2 = a/b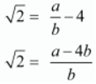
√2 is rational number which is a contradication.
Hence 4 + √2 is irrational.
(iv) 5√2
Ans. Let us assume that 5√2 is rational .Then , there exist positive co primes a and b such that
5√2 = a / b
√2 is rational number which is a contradication.
Hence 5√2 is irrational.
Q.3. Show that 2 − √3 is an irrational number.
Ans. Let us assume that 2 − √3 is rational .Then, there exist positive co primes a and b such that
2 − √3 = a/b
√3 = 2 − a/b
This implies,
√3 is a rational number, which is a contradiction.
Hence, 2 − √3 is irrational number.
Q.4. Show that 3 + √2 is an irrational number.
Ans. Let us assume that 3 + √2 is rational .Then, there exist positive co primes a and b such that
3 + √2 = a/b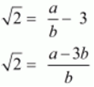
This implies,
√2 is a rational number, which is a contradiction.
Hence, 3 + √2 is irrational number.
Q.5. Prove that 4 - 5√2 is an irrational number.
Ans. Let us assume that 4 - 5√2 is rational .Then, there exist positive co primes a and b such that
4 - 5√2 = a / b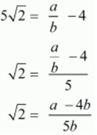
This contradiction the fact that √2 is an irrational
Hence, 4 - 5√2 is irrational number.
Q.6. Show that 5 - 2√3 is an irrational number.
Ans. Let us assume that 5 - 2√3 is rational .Then, there exist positive co primes a and b such that
5 - 2√3 = a / b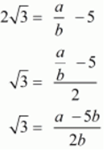
This contradiction the fact that √3 is an irrational
Hence, 5 - 2√3 is irrational number.
Q.7. Prove that 2√3 - 1 is an irrational number.
Ans. Let us assume that 2√3 - 1 is rational .Then, there exist positive co primes a and b such that
2√3 - 1 = a / b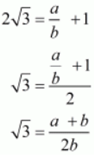
This contradiction the fact that √3 is an irrational
Hence, 2√3 - 1 is irrational number.
Q.8. Prove that 2 - 3√5 is an irrational number.
Ans. Let us assume that 2 - 3√5 is rational .Then, there exist positive co primes a and b such that
2 - 3√5 = a / b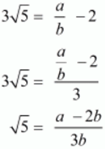
This contradiction the fact that √5 is an irrational
Hence, 2 - 3√5 is irrational number.
Q.9. Prove that √5 + √3 is irrational.
Ans. Let us assume that √5 + √3 is rational .Then, there exist positive co primes a and b such that
√5 + √3 = a / b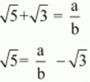
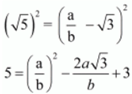
⇒ 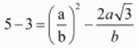
⇒ 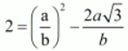
⇒ 
⇒ 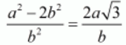
⇒ 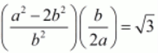
⇒ 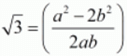
Here we see that √3 is a rational number which is a contradiction as we know that √3 is an irrational number.
Hence, √5 + √3 is irrational number.
Q.10. Prove that √2 + √3 is an irrational number.
Ans. Let us assume that √2 + √3 is rational . Then, there exist co-prime positive integers a and b such that
√2 + √3 = a / b
Squaring on both sides, we get 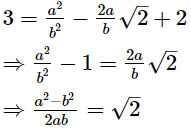
⇒ √2 is a rational number (a,b are integers, so a2 - b2/2ab is rational)
This contradicts the fact that √2 is a rational number. So our assumption was incorrect. Hence, √2 + √3 is an irrational number.
Q.11. Given that √2 is irrational, prove that (5 + 3√2) is an irrational number.
Ans. Let us assume, to the contrary that 5 + 3√2 is rational
That is, we can find co-prime a and b (b ≠ 0) such that 5 + 3√2 = ab Therefore,
5 - a/b = -3√2
Since, a and b are integers, we get a - 5b/3b is rational, and so √2 is rational.
which contradicts the fact that √2 is irrational.
So, our assumption was wrong that 5 + 3√2 is rational.
Hence, we conclude that 5 + 3√2 is irrational.
Q.12. Prove that 2 + √3/5 is an irrational number, given that √3 is an irrational number.
Ans. Let us assume that (2 + √3)/5 is a rational number.
Thus, (2 + √3)/5 can be represented in the form of p/q, where p and q both are integers, q ≠ 0, p and q are co-prime numbers.
(2 + √3)/5 = p/q
⇒ 2 + √3 = 5(p/q)
since, 5p - 2q/q is rational ⇒ √3 is rational.
But, it is given that √3 is an irrational number.
Therefore, our assumption is wrong.
Hence, (2 + √3)/5 is an irrational number.
FAQs on Chapter 1 - Real Numbers, RD Sharma Solutions - (Part - 7) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are real numbers in mathematics? |  |
| 2. How do you distinguish between rational and irrational numbers? |  |
| 3. How can real numbers be classified into different categories? |  |
| 4. Can you provide examples of real numbers that are not rational? |  |
| 5. How are real numbers used in practical applications outside of mathematics? |  |

|
Explore Courses for Class 10 exam
|

|
















