Chapter 10 - Circles, RD Sharma Solutions - (Part - 2) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 8.34
Q.13. In a right triangle ABC in which ∠B = 90° , a circle is drawn with AB as diameter intersecting the hypotenuse AC at P . Prove that the tangent to the circle at P bisects BC.
Ans.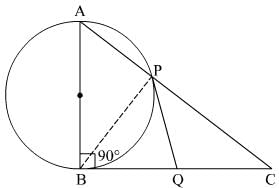
Given: ΔABC is right triangle in which ∠ABC = 90°. A circle is drawn with side AB as diameter intersecting AC in P.
PQ is the tangent to the circle when intersects BC in Q.
Construction: Join BP.
Proof:
PQ and BQ are tangents drawn from an external point Q.
⇒ PQ = BQ .....(i) [Length of tangents drawn from an external point to the circle are equal]
⇒ ∠PBQ = ∠BPQ [In a triangle, equal sides have equal angles opposite to them]
As , it is given that,
AB is the diameter of the circle.
∴ ∠APB = 90° [Angle in a semi-circle is 90°]
∠APB + ∠BPC = 180° [Linear pair]
⇒ ∠BPC = 180° – ∠APB = 180° – 90° = 90°
In ΔBPC,
∠BPC + ∠PBC + ∠PCB = 180° [Angle sum property]
⇒ ∠PBC + ∠PCB = 180° – ∠BPC = 180° – 90° = 90° ....(ii)
Now,
∠BPC = 90°
⇒ ∠BPQ + ∠CPQ = 90° .....(iii)
From (ii) and (iii), we get,
⇒ ∠PBC + ∠PCB = ∠BPQ + ∠CPQ
⇒ ∠PCQ = ∠CPQ [∠BPQ = ∠PBQ]
In ΔPQC,
∠PCQ = ∠CPQ
∴ PQ = QC .....(iv)
From (i) and (iv), we get,
BQ = QC
Thus, tangent at P bisects the side BC.
Q.14. From an external point P, tangents PA and PB are drawn to a circle with centre O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of Δ PCD.
Ans. Let us first put the given data in the form of a diagram.
It is given that PA = 14cm. we have to find the perimeter of ΔPCD
Perimeter of ΔPCD is PC + CD + PD
Looking at the figure we can rewrite the equation as follows.
Perimeter of ΔPCD is PC + CE + ED + PD ……(1)
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,
CE =CA
ED =DB
Replacing the above in equation (1), we have,
Perimeter of ΔPCD as PC + CA + DB + PD
By looking at the figure we get,
PC +CA =PA
DB +PD =PB
Therefore,
Perimeter of ΔPCD is PA + PB
It is given that PA = 14 cm. again from the same property of tangents which says that the length of two tangents drawn to a circle from the same external point will be equal, we have,
PA = PB
Therefore,
Perimeter of ΔPCD = 2PA
Perimeter of ΔPCD = 2 × 14
Perimeter of ΔPCD = 28
Thus perimeter of ΔPCD is 28 cm.
Q.15. In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.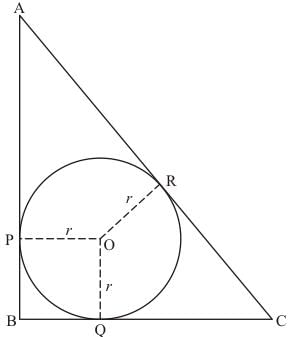
Ans. From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore, we have
BQ = BP
Let us denote BP and BQ by x
AP = AR
Let us denote AP and AR by y
RC = QC
Let us denote RC and RQ by z
We have been given that ΔABC is a right triangle and BC = 6 cm and AB = 8 cm. let us find out AC using Pythagoras theorem. We have,
AC2 = AB2 + BC2
AC2 = 62 + 82
AC2 = 36 + 64
AC2 = 100
AC = √100
AC = 10
Consider the perimeter of the given triangle. We have,
AB + BC + AC = 8 + 6 + 10
AB + BC + AC = 24
Looking at the figure, we can rewrite it as,
AP + PB + BQ + QC + AR + RC = 24
Let us replace the sides with the respective x, y and z which we have decided to use.
y + x + x + z + y + z = 24
2x + 2y + 2z = 24
2(x + y + z) = 24
x + y + z = 12 .....(1)
Now, consider the side AC of the triangle.
AC = 10
Looking at the figure we can say,
AR + RC = 10
y + z = 10 …… (2)
Now let us subtract equation (2) from equation (1). We have,
x + y + z = 12
y + z = 10
After subtracting we get,
x = 2
That is,
BQ = 2, and
BP = 2
Now consider the quadrilateral BPOQ. We have,
BP = BQ (since length of two tangents drawn to a circle from the same external point are equal)
Also,
PO = OQ (radii of the same circle)
It is given that ∠PBQ = 90°
From the property of tangents, we know that the tangent will be at right angle to the radius of the circle at the point of contact. Therefore,
∠OPB = 90°
∠OQB = 90°
We know that sum of all angles of a quadrilateral will be equal to 360°. Therefore,
∠PBQ + ∠OPB + ∠OQB + ∠POQ = 360°
90° + 90° + 90° ∠POQ = 360°
270° + ∠POQ = 360°
∠POQ = 90°
Since all the angles of the quadrilateral are equal to 90°
and the adjacent sides also equal, this quadrilateral is a square. Therefore, all sides will be equal. We have found out that,
BP = 2 cm
Therefore, the radii
PO = 2 cm
Thus the radius of the incircle of the triangle is 2 cm.
Page No 8.35
Q.16. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Ans.
In the given figure, C is the mid point of the minor arc AB of the circle with centre O.
PQ is the tangent to the given circle through point C.
To Prove: Tangent drawn at the mid point of the arc  of a circle is parallel to the chord joining the end point of the arc
of a circle is parallel to the chord joining the end point of the arc i.e AB || PQ.
i.e AB || PQ.
Proof: C is the mid point of the minor arc AB
⇒ minor arc AC = minor arc BC
⇒ AC = BC
Thus, ∆ABC is an iscosceles triangle.
Therefore, the perpendicular bisector of side AB of ∆ABC passes through the vertex C.
We know that the perpendicular bisector of a chord passes through the centre of the circle.
Since AB is a chord of the circle so, the perpendicular bisector of AB passes through the centre O.
Thus, it is clear that the perpendicular bisector of AB passes through the points O and C.
Therefore, AB⊥OC
Now, PQ is the tangent to the circle through the point C on the circle.
Therefore, PQ⊥OC [Tangent to a circle is perpendicular to its radius through the point of contact]
Page No 8.35
Q.17. From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP = diameter of the circle, show that Δ APB is equilateral.
Ans. Let us first put the given data in the form of a diagram.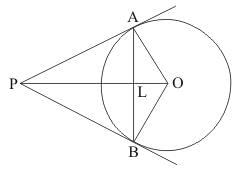
Consider ΔPOA and ΔPOB. We have,
PO is the common side for both the triangles.
PA = PB(Tangents drawn from an external point will be equal in length)
OB = OA(Radii of the same circle)
Therefore, by SSS postulate of congruency, we have
ΔPOA ≅ ΔPOB
Hence,
∠OPA = ∠OPB …… (1)
Now let us consider ΔPLA and ΔPLB . We have,
PL is the common side for both the triangles.
∠OPA = ∠OPB (From equation (1))
PA = PB (Tangents drawn from an external point will be equal in length)
From SAS postulate of congruent triangles,
ΔPLA ≅ ΔPLB
Therefore,
PL = LB …… (2)
∠PLA = ∠PLB
Since AB is a straight line,
∠ALB = 180°
∠PLA + ∠PLB = 180°
2∠PLA = 180°
∠PLA = 90°
∠PLB = 90°
Let us now take up ΔOPB. We know that the radius of a circle will always be perpendicular to the tangent at the point of contact. Therefore,
∠OBP = 90°
By Pythagoras theorem we have,
PB2 = OP2 - OB2
It is given that
OP = diameter of the circle
Therefore,
OP = 2OB
Hence,
PB2 = (2OB)2 - OB2
PB2 = 4OB2 - OB2
PB2 = 3OB2
PB = √3OB
Consider ΔPLB . We have,
LB2 = PB2 - PL2
But we have found that,
PB = √3OB
Also from the figure, we can say
PL = PO − OL
Therefore,
LB2 = 3OB2 - [PO - OL]2 .....(3)
Also, from ΔOLB , we have
LB2 = OB2 - OL2 .....(4)
Since Left Hand Sides of equation (3) and equation (4) are same, we can equate the Right Hand Sides of the two equations. Thus we have,
OB2 - OL2 = 3OB2 - [PO - OL]2
OB2 - OL2 = 3OB2 - [PO2 + OL2 - 2.PO.OL]
OB2 - OL2 = 3OB2 - PO2 - OL2 + 2.PO.OL
We know from the given data, that OP = 2.OB. Let us substitute 2OB in place of PO in the above equation. We get,
OB2 - OL2 = 3OB2 - (2OB)2 - OL2 + 2.2.OB.OL
OB2 - OL2 = 3OB2 - 4OB2 - OL2 + 4.OB.OL
2OB2 = 4.OB.OL
Substituting the value of OL and also PO in equation (3), we get,
Also from the figure we get,
AB = PL + LB
From equation (2), we know that PL = LB. Therefore,
AB = 2.LB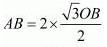
AB = √3OB
We have also found that PB = √3OB.
We know that tangents drawn from an external point will be equal in length. Therefore, we have
PA = PB
Hence,
PA = √3OB
Now, consider ΔPAB. We have,
PA = √3OB
PB = √3OB
AB = √3OB
Since all the sides of the triangle are of equal length,ΔPAB is an equilateral triangle. Thus we have proved.
Q.18. Two tangent segments PA and PB are drawn to a circle with centre O such that ∠APB = 120°. Prove that OP = 2 AP.
Ans. Let us first put the given data in the form of a diagram. We have,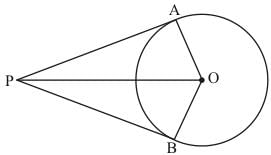
Consider ΔPAO and ΔPBO. We have,
Here, PO is the common side.
PA = PB (Length of two tangents drawn from the same external point will be equal)
OA = OB(Radii of the same circle)
By SSS congruency, we have ΔPAO is congruent to ΔPBO.
Therefore,
∠APO = ∠BPO
It is given that,
∠APB = 120°
That is,
∠APO + ∠BPO = 120°
2∠APO = 120°(Since ∠APO = ∠BPO)
∠APO = 60°
In ΔPAO,
∠PAO = 90°(Since radius will be perpendicular to the tangent at the point of contact)
We know that,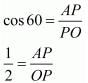
OP = 2AP
Thus we have proved.
Q.19. If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
Ans. Let us first put the given data in the form of a diagram.
It is given that triangle ABC is isosceles with
AB = AC …… (1)
By looking at the figure we can rewrite the above equation as,
AM + MB = AN + NC
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,
AM = AN
Let us substitute AN with AM in the equation (1). We get,
AM + MB = AM + NC
MB = NC …… (2)
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,
MB = BL
NC = LC
But from equation (2), we have found that
MB = NC
Therefore,
BL = LC
Thus we have proved that point L bisects side BC.
Q.20. AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC= 30∘ . The tangent at C intersects AB at a point D . Prove that BC = BD.
Ans.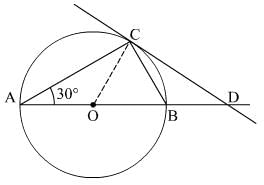
It is given that ∠BAC = 30° and AB is diameter.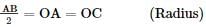
∠ACB = 90° (Angle formed by the diameter is 90°)
In ∆ABC,
∠ACB + ∠BAC + ∠ABC = 180°
⇒ 90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
⇒ ∠CBD = 180° – 60° = 120° ( ∠CBD and ∠ABC form a linear pair)
In ∆OCD,
∠OCD = 90° (Angle made by Radius on the tangent)
∠OBC = ∠ABC = 60°
Since OB = OC, ∠OCB = ∠OBC = 60° (OC = OB = radius)
In ∆OCB,
⇒ ∠COB + ∠OCB + ∠OBC = 180°
⇒ ∠COB + 60° + 60° = 180°
⇒ ∠COB = 60°
In ∆OCD,
∠COD + ∠OCD + ∠ODC = 180°
⇒ 60° + 90° + ∠ODC = 90° (∠COD = ∠COB)
⇒ ∠ODC = 30°
In ∆CBD,
∠CBD = 120°
∠BDC = ∠ODC = 30°
⇒ ∠BCD + ∠BDC + ∠CBD = 180°
⇒ ∠BCD + 30° + 120° = 180°
⇒ ∠BCD + 30° = ∠BDC
Angles made by BC and BD on CD are equal, so ∆CBD is an isosceles triangle and therefore, BC = BD.
FAQs on Chapter 10 - Circles, RD Sharma Solutions - (Part - 2) - RD Sharma Solutions for Class 10 Mathematics
| 1. What is the relationship between the radius and diameter of a circle? |  |
| 2. How do you find the circumference of a circle if you know its radius? |  |
| 3. What is the formula to calculate the area of a circle? |  |
| 4. How many degrees are in a complete circle? |  |
| 5. Can a circle have an infinite number of tangents? |  |

|
Explore Courses for Class 10 exam
|

|
















