Chapter 2 - Polynomials, RD Sharma Solutions - (Part-5) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.57
Ques.5. Obtain all zeros of the polynomial f(x) = x4 − 3x3 − x2 + 9x − 6, if two of its zeros are -√3 and √3
Ans. We know that if x =α is a zero of a polynomial, then (x - α) is a factor of f(x).
Since -√3 and √3 are zeros of f(x).
Therefore
(x + √3)(x - √3) = x2 + √3x - √3x - 3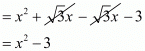
x2 - 3 is a factor of f(x). Now, we divide f(x) = x4 - 3x3 - x2 + 9x - 6 by g(x) = x2 - 3 to find the other zeros of f(x).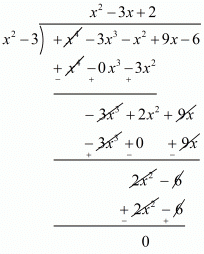
By using division algorithm we have, 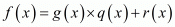 .
. 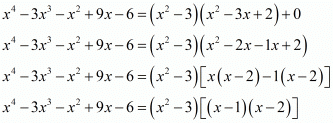
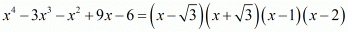
Hence, the zeros of the given polynomials are -√3, +√3, +1, +2.
Ques.6. Find all zeros of the polynomial f(x) = 2x4 − 2x3 − 7x2 + 3x + 6, if its two zeros are 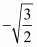 and
and 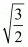
Ans. Since 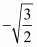 and
and 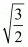 are two zeros of f(x).Therefore,
are two zeros of f(x).Therefore, 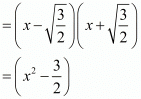
= 1/2(2x2 - 3) is a factor of f(x).
Also 2x2 - 3 is a factor of f(x).
Let us now divide f(x) by 2x2 - 3. We have, 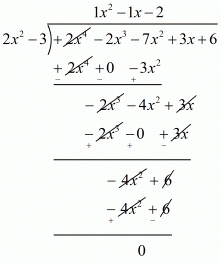
By using division algorithm we have, 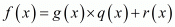
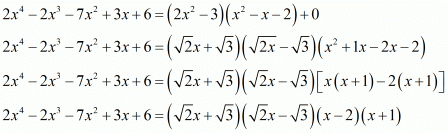
Hence, The zeros of f(x) are 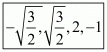 .
.
Ques.7. Find all the zeros of the polynomial x4 + x3 − 34x2 − 4x + 120, if two of its zeros are 2 and −2.
Ans. We know that if x =α is a zero of a polynomial, then x - α is a factor of f(x).
Since, 2 and -2 are zeros of f(x).
Therefore
(x + 2)(x - 2) = x2 - 22
= x2 - 4
x2 - 4 is a factor of f(x). Now, we divide x4 + x3 - 34x2 - 4x + 120 by g(x) = x2 - 4 to find the other zeros of f(x). 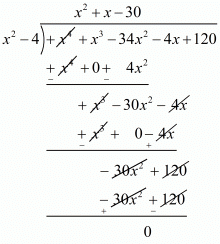
By using division algorithm we have 
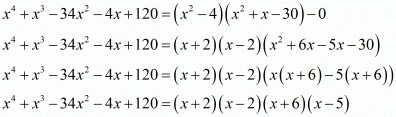
Hence, the zeros of the given polynomial are -2, +2, -6, and 5.
Ques.8. Find all zeros of the polynomial 2x4 + 7x3 − 19x2 − 14x + 30, if two of its zeros are √2 and -√2.
Ans. We know that if x = α is a zero of a polynomial, and then x - α is a factor of f(x).
Since √2 and -√2 are zeros of f(x).
Therefore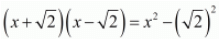
= x2 - 2
x2 - 2 is a factor of f(x). Now, we divide 2x4 + 7x3 - 19x2 - 14x + 30 by g(x) = x2 - 2 to find the zero of f(x).
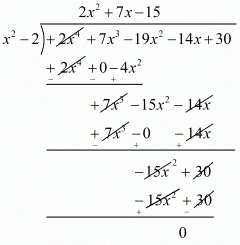
By using division algorithm we have 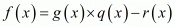
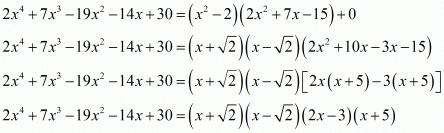
Hence, the zeros of the given polynomial are 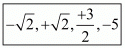 .
.
Page No 2.58
Ques.9. Find all the zeros of the polynomial 2x3 + x2 − 6x − 3, if two of its zeros are −√3 and √3.
Ans. We know that if x = α is a zero of a polynomial, and then x -α is a factor of f(x).
Since √3 and -√3 are zeros of f(x).
Therefore
(x + √3)(x - √3) = x2 - 3
= x2 - 3
x2 - 3 is a factor of f(x).Now, we divide 2x3 + x2 - 6x - 3 by g(x) = x2 - 3 to find the other zeros of f(x). 
By using division algorithm we have 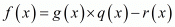
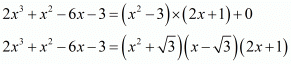
Hence, the zeros of the given polynomial are .
.
Ques.10. Find all the zeros of the polynomial x3 + 3x2 − 2x − 6, if two of its zeros are -√2 and √2.
Ans. We know that if x = α is a zero of a polynomial, and then x - α is a factor of f(x).
Since √2 and -√2 are zeros of f(x).
Therefore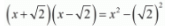
=x2 - 2
x2 - 2 is a factor of f(x).Now, we divide x3 + 3x2 - 2x - 6 by g(x) = x2 - 2 to find the other zeros of f(x). 
By using division algorithm we have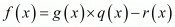
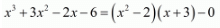
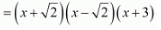
Hence, the zeros of the given polynomials are -√2, +√2, and -3.
Ques.11. Find all zeros of the polynomial 2x4 – 9x3 + 5x2 +3x – 1, if two of its zeros are 2+√3 and 2−√3.
Ans. It is given that 2+√3 and 2−√3 are two zeroes of the polynomial f(x) = 2x4 – 9x3 + 5x2 + 3x – 1.
∴ {x - (2 + √3)}{x - (2 - √3)}=(x - 2 -√3)(x - 2 +√3)
= (x−2)2−(√3)2
= x2 − 4x + 4 − 3
= x2 − 4x + 1
is a factor of f(x)
Now, divide f(x) by x2 – 4x + 1.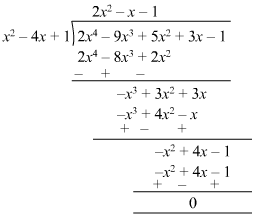
∴ f(x) = (x2 – 4x + 1) (2x2 – x – 1)
Hence, other two zeroes of f(x) are the zeroes of the polynomial 2x2 – x – 1.
2x2 – x – 1 = 2x2 – 2x + x – 1 = 2x(x – 1) + 1 (x – 1) = (2x + 1) (x – 1)
Hence, the other two zeroes are −1/2 and 1.
Ques.12. For what value of k, is the polynomial f(x) = 3x4 – 9x3 + x2 + 15x + k completely divisible by 3x2 – 5?
Ans. Let f(x) = 3x4 – 9x3 + x2 + 15x + k
It is given that f(x) is completely divisible by 3x2 – 5.
Therefore, one factor of f(x) is (3x2 – 5).
We get another factor of f(x) by dividing it with (3x2 – 5).
On division, we get the quotient x2 – 3x + 2 and the remainder k + 10.
Since, f(x) = 3x4 – 9x3 + x2 + 15x + k completely divisible by 3x2 – 5
Therefore, remainder must be zero.
⇒ k + 10 = 0
⇒ k = −10
Hence, the value of k is –10.
Ques.13. What must be added to the polynomial f(x) = x4 + 2x3 − 2x2 + x − 1 so that the resulting polynomial is exactly divisible by x2 + 2x − 3?
Ans. We know that,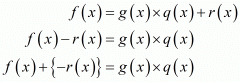
Clearly , Right hand side is divisible by g(x).
Therefore, Left hand side is also divisible by g(x). Thus, if we add -r(x) to f(x), then the resulting polynomial is divisible by g(x).
Let us now find the remainder when f(x) is divided by g(x).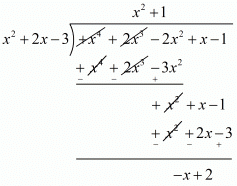
Hence, we should add -r(x) = x - 2 to f(x) so that the resulting polynomial is divisible by g(x).
Ques.14. What must be subtracted from the polynomial f(x) = x4 + 2x3 − 13x2 − 12x + 21 so that the resulting polynomial is exactly divisible by x2 − 4x + 3?
Ans. We know that Dividend = Quotient x Divisor + Remainder.
Dividend - Remainder = Quotient x Divisor.
Clearly, Right hand side of the above result is divisible by the divisor.
Therefore, left hand side is also divisible by the divisor.
Thus, if we subtract remainder from the dividend, then it will be exactly divisible by the divisor.
Dividing x4 + 2x3 - 13x2 - 12x + 21 by x2 - 4x + 3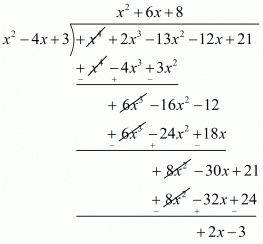
Therefore, quotient = x2 + 6x + 8 and remainder = (2x - 3).
Thus, if we subtract the remainder 2x - 3 from x4 + 2x3 - 13x2 - 12x + 21, it will be divisible by x2 - 4x + 3.
Ques.15. Given that √2 is a zero of the cubic polynomial 6x3 + √2x2 − 10x − 4√2, find its other two zeroes.
Ans. We know that if x = α is a zero of a polynomial, and then x - α is a factor of f(x).
It is given the √2 is a zero of the cubic polynomial f(x) = 6x3 + √2x2 − 10x − 4√2.
Therefore, x − √2 is a factor of f(x). Now, we divide 6x3 + √2x2 − 10x − 4√2 by x−√2 to find the other zeroes of f(x).
∴ Quotient = 6x2 + 7√2x + 4 and remainder = 0.
By using division algorithm, we have f(x) = g(x) × q(x) + r(x).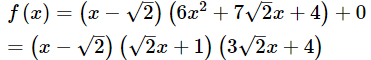
Hence, the other two zeroes of the given polynomial are -(1/√2) and -(4/3√2).
Ques.16. Given that x − √5 is a factor of the cubic polynomial x3 − 3√5x2 + 13x − 3√5, find all the zeroes of the polynomial.
Ans. We know that if x = α is a zero of a polynomial, and then x - α is a factor of f(x).
It is given that x − √5 is a factor of f(x) = x3− 3√5x2 + 13x − 3√5.
Now, we divide x3−3√5x2 + 13x − 3√5 by x−√5 to find the other zeroes of f(x).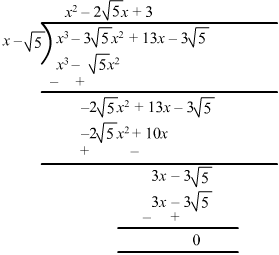
∴ Quotient = x2 − 2√5x + 3 and remainder = 0.
By using division algorithm, we have 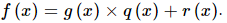
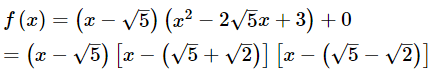
Hence, the zeroes of the given polynomial are √5, √5 + √2 and √5 − √2.
Page No 2.58
Ques.1. If α, β are the zeros of the polynomial f(x) = x2 + x + 1, then 
(a) 1
(b) −1
(c) 0
(d) None of these
Ans. Since α and β are the zeros of the quadratic polynomial f(x) = x2 + x + 1
α + β = -(coefficient of x / coefficient of x2)
= ((-1)/1) = 1
α x β = constant term/coefficient of x2
= 1/1 = 1
We have
The value of 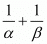 is -1
is -1
Hence, the correct choice is (b).
Ques.2. If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then 1/α + 1/β is equal to
(a) 7/3
(b) -(7/3)
(c) 3/7
(d) -(3/7)
Ans. Since α and β are the zeros of the quadratic polynomial p(x) = 4x2 + 3x + 7
α + β = ((-coefficient of x) / coefficient of x2)
= (-3)/4
αβ = constant term/coefficient of x2
= 7/4
We have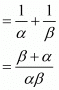
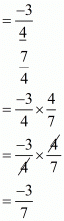
The value of 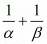 is (-3)/7.
is (-3)/7.
Hence, the correct choice is d.
Ques.3. If one zero of the polynomial f(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of the other, then k =
(a) 2
(b) −2
(c) 1
(d) −1
Ans. We are given f(x) = (k2 + 4)x2 + 13x + 4k then
α + β = ((-coefficient of x) / coefficient of x2)
α x β = constant term/coefficient of x2
One root of the polynomial is reciprocal of the other. Then, we have
α x β = 1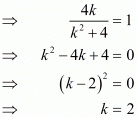
Hence the correct choice is a.
Ques.4. If the sum of the zeros of the polynomial f(x) = 2x3 − 3kx2 + 4x − 5 is 6, then the value of k is
(a) 2
(b) 4
(c) −2
(d) −4
Ans. Let α, β be the zeros of the polynomial f(x) = 2x3 - 3kx2 + 4x - 5 and we are given that α + β + γ = 6.
Then,
α + β + γ = −Coefficient of x/Coefficient of x2
= -((-3k)/2) = 3k/2
It is given that
α + β + γ = 6
Substituting α + β + γ = 3k/2, we get
The value of k is 4.
Hence, the correct alternative is b.
Ques.5. If α and β are the zeros of the polynomial f(x) = x2 + px + q, then a polynomial having 1/α and 1/β is its zero is
(a) x2 + qx + p
(b) x2 − px + q
(c) qx2 + px + 1
(d) px2 + qx + 1
Ans. Let α and β be the zeros of the polynomial f(x) = x2 + px + q. Then,
α + β = −Coefficient of x/Coefficient of x2
= -(p/1)
= -p
And
αβ = constant term/coefficient of x2
= q/1
= q
Let S and R denote respectively the sum and product of the zeros of a polynomial
Whose zeros are 1/α and 1/β then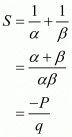

Hence, the required polynomial g(x) whose sum and product of zeros are S and R is given by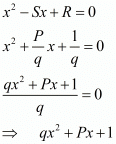
So g(x) = qx2 + Px + 1
Hence, the correct choice is c.
Ques.6. If α, β are the zeros of polynomial f(x) = x2 − p (x + 1) − c, then (α + 1) (β + 1) =
(a) c − 1
(b) 1 − c
(c) c
(d) 1 + c
Ans. Since α and β are the zeros of quadratic polynomial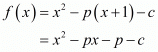
α + β = −Coefficient of x/Coefficient of x2
= - ((-p)/1)
= p
α x β = constant term/coefficient of x2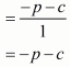
We have
(α + 1)(β + 1)
= -c + 1
= 1 - c
The value of (α + 1)(β + 1) is 1 - c.
Hence, the correct choice is b.
Ques.7. If α, β are the zeros of the polynomial f(x) = x2 − p(x + 1) − c such that (α +1) (β + 1) = 0, then c =
(a) 1
(b) 0
(c) −1
(d) 2
Ans. Since α and β are the zeros of quadratic polynomial
f(x) = x2 - p(x+1) - c
f(x) = x2 - px - p - c
α + β = ((−Coefficient of x)/Coefficient of x2)
= -((-p)/1)
= p
αβ = constant term/coefficient of x2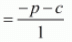
= -p-c
We have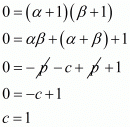
The value of c is 1.
Hence, the correct alternative is a.
Ques.8. If f(x) = ax2 + bx + c has no real zeros and a + b + c = 0, then
(a) c = 0
(b) c > 0
(c) c < 0
(d) None of these
Ans. If f(x) = ax2 + bx + c has no real zeros and a + b + c < 0 then c < 0
Hence, the correct choice is c.

|
Explore Courses for Class 10 exam
|

|

















