Open App

Class 10 Exam > Class 10 Notes > Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9)

Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10 PDF Download

Page No 5.30

Ques.11. Split 207 into three parts such that these are in A.P. and the product of the two smaller parts is 4623.
Ans. Suppose three parts of 207 are (a − d), a , (a + d) such that, (a + d) > a > (a − d).
a − d + a + a + d = 207
⇒ 3a = 207
⇒ a = 69
Now, (a − d) × a = 4623
⇒ 69(69 − d) = 4623
⇒ (69 − d) = 67
⇒ d = 2
Therefore, the three required parts are 67, 69 and 71.

Ques.12. The angles of a triangle are in A.P. The greatest angle is twice the least. Find all the angles.
Ans. Suppose the angles of a triangle are (a − d), a, (a + d) such that, (a + d) > a > (a − d).
a − d + a + a + d =180 [angle sum property]
⇒ 3a = 180
⇒ a = 60
Now, (a + d) = 2(a − d)
⇒ a + d = 2a − 2d
⇒ a = 3d
⇒ d = 60/3 = 20
Therefore, the three angles of a triangle are 40, 60, 80.

Ques.13. The sum of four consecutive numbers in A.P. is 32 and the ratio of the product of the first and last terms to the product of two middle terms is 7 : 15. Find the number.
Ans. Let the four terms of the AP be a − 3d, a − d, a + d and a + 3d.
Given:
(a − 3d) + (a − d) + (a + d) + (a + 3d) = 32
⇒ 4a = 32
⇒ a = 8
Also,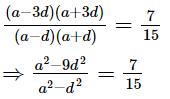
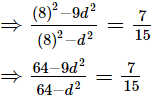
Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10

⇒ 960 − 135d² = 448 − 7d²
⇒ 512 = 128d²
⇒ d² = 4
⇒ d = ±2
When a = 8 and d= 2, then the terms are 2, 6, 10, 14.
When a = 8 and d= −2, then the terms are 14, 10, 6, 2.

Page No 5.50

Ques.1. Find the sum of the following arithmetic progressions:
(i) 50, 46, 42, ... to 10 terms
(ii) 1, 3, 5, 7, ... to 12 terms
(iii) 3, 9/2, 6, 15/2, ... to 25 terms
(iv) 41, 36, 31, ... to 12 terms
(v) a + b, a − b, a − 3b, ... to 22 terms
(vi) (x − y)², (x² + y²), (x + y)², ..., to n terms
(vii) 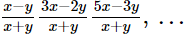to n terms
(viii) −26, −24, −22, ... to 36 terms.
Ans. In the given problem, we need to find the sum of terms for different arithmetic progressions. So, here we use the following formula for the sum of n terms of an A.P.,
S_n = (n/2)[2a + (n - 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
(i) 50, 46, 42, ... To 10 terms
Common difference of the A.P. (d)
= a₂ -a₁
= 46 - 50
= -4
Number of terms (n) = 10
First-term for the given A.P. (a) = 50
So, using the formula we get,
S₁₀ = (10/2)[2(50) + (10-1)(-4)]
= (5)[100 + (9)(-4)]
= (5)[100 - 36]
= (5)[64]
= 320
Therefore, the sum of first 10 terms for the given A.P. is 320.
(ii) 1, 3, 5, 7, ... - 26 To 12 terms.
Common difference of the A.P. (d)
= a₂ - a₁
= 3 - 1
= 2
Number of terms (n) = 12
First-term for the given A.P. (a) = 1
So, using the formula we get,
S_n = (12/2)[2(1) + (12 - 1)(2)]
= (6)[2 + (11)(2)]
= (6)[2 + 22]
= (6([24]
= 144
Therefore, the sum of first 12 terms for the given A.P. is 144.
(iii) 3, 9/2, 6, 15/2, ... To 25 terms.
Common difference of the A.P. (d) = a₂ - a₁
= (9/2) - 3
= Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
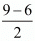
= 3/2
Number of terms (n) = 25
First term for the given A.P. (a) = 3
So, using the formula we get,
S₂₅ = (25/2)[2(3) + (25 - 1)(3/2)]
= (25/2)[6 + (24)(3/2)]
= (25/2)[6 + (72/2)]
= (25/2)[6 + 36]
= (25/2)[42]
= (25)(21)
= 525
On further simplifying, we get,
S₂₅ = 525
Therefore, the sum of first 25 terms for the given A.P. is 525.
(iv) 41, 36, 31, ... To 12 terms.
Common difference of the A.P. (d) = a₂ - a₁
36 - 41
= -5
Number of terms (n) = 12
First-term for the given A.P. (a) = 41
So, using the formula we get,
S₁₂ = 12/2[2(41) + (12 - 1)(-5)]
= (6)[82 + (11)(-5)]
= (6)[82 - 55]
= (6)[27]
= 162
Therefore, the sum of first 12 terms for the given A.P. is 162.
(v) a + b, a - b, a - 3b, ... To 22 terms.
Common difference of the A.P. (d) = a₂ - a₁
= (a - b)-(a + b)
= a - b - a - b
= -2b
Number of terms (n) = 22
First-term for the given A.P. (a) = a + b
So, using the formula we get,
S₂₂ = 22/2[2(a + b) + (22 - 1)(-2b)]
= (11)[2a + 2b + (21)(-2b)]
= (11)[2a + 2b - 42b]
= (11)[2a - 40b]
= 22a - 440b
Therefore, the sum of first 22 terms for the given A.P. is 22a - 440b.
(vi) (x − y)², (x² + y²), (x + y)², ..., To n terms.
Common difference of the A.P. (d) = a₂ - a₁
= (x² + y²)-(x - y)²
= x² + y² - (x² + y² - 2xy)
= x² + y² - x² - y² + 2xy
= 2xy
Number of terms (n) = n
First-term for the given A.P. (a) = (x - y)²
So, using the formula we get,
S_n = n/2[2(x - y)² + (n - 1)2xy]
Now, taking 2 common from both the terms inside the bracket we get,
=(n/2)[(2)(x - y)² + (2)(n - 1)xy]
=(n/2)(2)[(x - y)² + (n - 1)xy]
= (n)[(x - y)² + (n - 1)xy]
Therefore, the sum of first n terms for the given A.P. is (n) [(x - y)² + (n - 1)xy]
(vii) Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10 To n terms.
Number of terms (n) = n
First-term for the given A.P. (a) =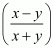
Common difference of the A.P. (d) = a₂ - a₁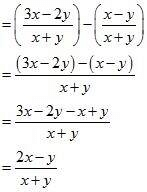

So, using the formula we get,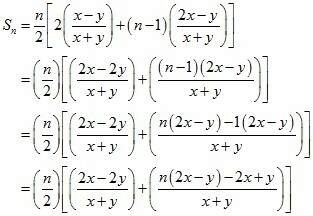

Now, on further solving the above equation we get,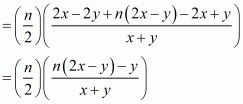

Therefore, the sum of first n terms for the given A.P. is Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10 .
(viii) -26, -24, -22, ... To 36 terms.
Common difference of the A.P. (d) = a₂ - a₁
_{= (-24)-(-26)}
_{= -24 + 26}_{= 2}
Number of terms (n) = 36
First-term for the given A.P. (a) = −26
So, using the formula we get,
S₃₆ = 36/2[2(-26) + (36 - 1)(2)]
= (18)[-52 + (35)(2)]
= (18)[-52 + 70]
= (18)[18]
= 324
Therefore, the sum of first 36 terms for the given A.P. is 324.

Page No. 5.5

Ques.1. Write the first five terms of each of the following sequences whose nth terms are:
(a) a_n = 3n + 2
(b) a_n =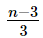
(c) a_n = 3ⁿ
(d) a_n=
(e) a_n = (−1)ⁿ 2ⁿ
(f) a_n=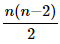
(g) a_n = n² − n + 1
(h) a_n = 2n²− 3n + 1
(i) a_n=
Ans. Here, we are given the n^th term for various sequences. We need to find the first five terms of the sequence.
(i) a_n = 3n + 2
Here, the n^th term is given by the above expression. So, to find the first term we use n = 1, we get,
a₁ = 3(1) + 2
= 3 + 2
= 5
Similarly, we find the other four terms,
Second term (n = 2),
a₂ = 3(2) + 2
= 6 + 2 = 8
Third term (n = 3),
a₃ = 3(3) + 2
= 9 + 2 = 11
Fourth term (n = 4),
a₄ = 3(4) + 2
= 12 + 2 = 14
Fifth term (n = 5),
a₅ = 3(5) + 2
= 15 + 2 = 17
Therefore, the first five terms for the given sequence are
a₁ = 5, a₂ = 8, a₃ = 11, a₄ = 14, a₅ = 17.
(ii) a_n = 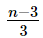Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
Here,the n^th term is given by the above expression. So, to find the first term we use, n = 1, we get,
a₁ = ((1) -(2))/3
= (-1)/3
Similarly, we find the other four terms,
Second term (n = 2),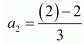

= 0/3
= 0
Third term (n = 3),
Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
Fourth term (n = 4),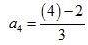

= 2/3
Fifth term (n= 5),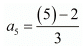

= 3/3 = 1
Therefore, the first five terms for the given sequence are.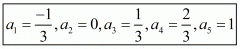
(iii) an = 3ⁿ
Here, the n^th term is given by the above expression. So, to find the first term we use n= 1,we get,
a1 = 3₍₁₎
= 3
Similarly, we find the other four terms,
Second term (n = 2)
a₂ = 3⁽²⁾
= (3)(3)
= 9
Third term = (n = 3),
a₃ = 3⁽³⁾
= (3)(3)(3)
= 27
Fourth term (n = 4)
a₄ = 3⁽⁴⁾
= (3)(3)(3)(3)
= 81
Fifth term (n = 5),
a₅ = 3⁽⁵⁾
= (3)(3)(3)(3)(3)
= 243
Therefore, the first five terms for the given sequence are a₁ = 3, a₂ = 9, a₃ = 27, a₄ = 81, a₅ = 243.
(iv) a_n=
Here, the n^th term is given by the above expression. So, to find the first term we use, n = 1, we get,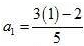
Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
= 1/5
Similarly, we find the other four terms,
Second term (n = 2),

Third term (n = 3),

Fourth term (n = 4),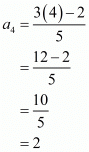

Fifth term (n = 5),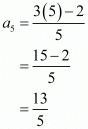

Therefore, the first five terms for the given sequence are.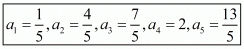
(v) a_n = (-1)ⁿ.2ⁿ
Here, the n^th term is given by the above expression. So, to find the first term we use n = 1, we get,
a₁ = (-1)¹.2¹
= (-1).2
= -2
Similarly, we find the other four terms,
Second term (n = 2),
a₂ = (-1)².2²
= 1.4 = 4
Third term (n = 3),
a₃ = (-1)³.2³
= (-1).8
= -8
Fourth term (n = 4),
a₄ = (-1)⁴.2⁴
= 1.16 = 16
Fifth term (n = 5),
a₅ = (-1)⁵.2⁵
=(-1).32 = -32
Therefore, the first five terms of the given A.P are a₁ = -2, a₂ = 4, a₃ = -8, a₄ = 16, a₅ = -32.
(vi) 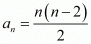Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
Here, the n^th term is given by the above expression. So, to find the first term we use n = 1, we get,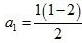

= (-1)/2
Similarly, we find the other four terms,
Second term (n = 2),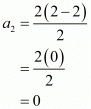

Third term(n = 3),

= 3/2
Fourth term (n = 4),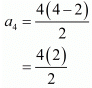

= 8/2 = 4
Fifth term (n = 5),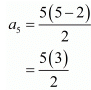
Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
= 15/2
Therefore, the first five terms for the given sequence are.
(vii) a_n = n² - n + 1
Here, the n^th term is given by the above expression. So, to find the first term we use n = 1, we get,
a₁ = (1)² - (1) + 1
= 1 - 1 + 1 = 1
Similarly, we find the other four terms,
Second term (n = 2),
a₂ = (2)² - (2) + 1
= 4 - 2 + 1 = 3
Third term (n = 3),
a₃ = (3)² - (3) + 1
= 9 - 3 + 1 = 7
Fourth term (n = 4),
a₄ = (4)² - (4) + 1
= 16 - 4 + 1 = 13
Fifth term (n = 5),
a₅ = (5)² - (5) + 1
= 25 - 5 + 1 = 21
Therefore, the first five terms for the given sequence are a₁ = 1, a₂ = 3, a₃ = 7, a₄ = 13, a₅ = 21.
(viii) a_n = 2a² - 3n + 1
Here, the n^th term is given by the above expression. So, to find the first term we use n = 1, we get,
a₁ = 2(1)² - 3(1) + 1
= 2(1) - 3 + 1
= 2 - 3 + 1= 0
Similarly, we find the other four terms,
Second term (n = 2),
a₂ = 2(2)² - 3(2) + 1
= 2(4) - 6 + 1
= 8 - 6 + 1 = 3
Third term (n = 3),
a₃ = 2(3)² - 3(3) + 1
= 2(9) - 9 + 1
= 18 - 9 + 1 = 10
Fourth term (n = 4),
a₄ = 2(4)² - 3(4) + 1
= 2(16) - 12 + 1
= 32 - 12 + 1 = 21
Fifth term (n = 5),
a₅ = 2(5)² - 3(5) + 1
= 2(25) - 15 + 1
= 50 - 15 + 1 = 36
Therefore, the first five terms for the given sequence are Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10 .
(ix)
Here, the n^th term is given by the above expression. So, to find the first term we use n = 1, we get,

Similarly, we find the other four terms,
Second term (n = 2),

Third term (n = 3),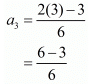

= 3/6 = 1/2
Fourth term (n = 4),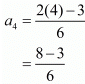
Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10
= 5/6
Fifth term (n = 5),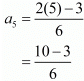

= 7/6
Therefore, the first five terms of the given A.P are.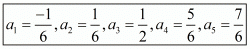

The document Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10 is a part of Class 10 category.

All you need of Class 10 at this link: Class 10

Top Courses for Class 10

View all

FAQs on Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10

1. What is the general form of a quadratic equation?

Ans. The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.

2. How can we solve a quadratic equation using the quadratic formula?

Ans. To solve a quadratic equation using the quadratic formula, we substitute the values of a, b, and c into the formula x = (-b ± √(b^2 - 4ac)) / 2a and simplify to find the roots of the equation.

3. What are the different methods to solve a quadratic equation?

Ans. There are several methods to solve a quadratic equation, including factoring, completing the square, using the quadratic formula, and graphing the equation to find the x-intercepts.

4. How can we determine the nature of the roots of a quadratic equation?

Ans. The nature of the roots of a quadratic equation can be determined by calculating the discriminant (b^2 - 4ac). If the discriminant is greater than 0, the equation has two distinct real roots. If it is equal to 0, the equation has one real root. If it is less than 0, the equation has two complex roots.

5. How can we use the roots of a quadratic equation to find the coefficients of the equation?

Ans. If α and β are the roots of a quadratic equation ax^2 + bx + c = 0, then the equation can be expressed as a(x - α)(x - β) = 0. By expanding this equation, we can equate the coefficients to find the values of a, b, and c.

Related Exams

Class 10

About this Document

Oct 31, 2024 Last updated

Document Description: Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) for Class 10 2024 is part of Class 10 preparation. The notes and questions for Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) have been prepared according to the Class 10 exam syllabus. Information about Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) covers topics like and Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Example, for Class 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9).

Introduction of Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) in English is available as part of our Class 10 preparation & Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) in Hindi for Class 10 courses. Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free. Class 10: Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10

Description

Full syllabus notes, lecture & questions for Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) - Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus | Best notes, free PDF download

Information about Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9)

In this doc you can find the meaning of Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) defined & explained in the simplest way possible. Besides explaining types of Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) theory, EduRev gives you an ample number of questions to practice Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) tests, examples and also practice Class 10 tests.

Download as PDF

Explore Courses for Class 10 exam

Top Courses for Class 10

Explore Courses

Signup for Free!

Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

Start learning for Free

10M+ students study on EduRev

Important questions

Viva Questions

study material

video lectures

past year papers

Extra Questions

RD Sharma Solutions - (Part-9) - Class 10

mock tests for examination

pdf

Sample Paper

Free

Chapter 5 - Quadratic Equations

Semester Notes

Exam

RD Sharma Solutions - (Part-9) - Class 10

Chapter 5 - Quadratic Equations

Previous Year Questions with Solutions

Objective type Questions

MCQs

practice quizzes

shortcuts and tricks

Chapter 5 - Quadratic Equations

ppt

Summary

RD Sharma Solutions - (Part-9) - Class 10

;

Additional Information about Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) for Class 10 Preparation

Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Free PDF Download

The Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) is an invaluable resource that delves deep into the core of the Class 10 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) now and kickstart your journey towards success in the Class 10 exam.

Importance of Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9)

The importance of Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) cannot be overstated, especially for Class 10 aspirants. This document holds the key to success in the Class 10 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Notes

Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Notes on EduRev are your ultimate resource for success.

Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Class 10 Questions

The "Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) on the App

Students of Class 10 can study Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-9) is prepared as per the latest Class 10 syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup