Chapter 6 - Triangles, RD Sharma Solutions - (Part - 1) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 7.118
Q.1. If the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is a right-angled triangle.
Ans. We have,
a = 3 cm
b = 4 cm
c = 6 cm
In order to prove that the triangle is a right angled triangle we have to prove that square of the larger side is equal to the sum of the squares of the other two sides.
Here, the larger side is c = 6 cm.
Hence, we have to prove that a2 + b2 = c2.
Let solve the left hand side of the above equation.
a2 + b2 = 32 + 42
= 9 + 16
= 25
Now we will solve the right hand side of the equation,
c2 = 62
= 36
Here we can observe that left hand side is not equal to the right hand side.
Therefore, the given triangle is not a right angled triangle.
Q.2. The sides of certain triangles are given below. Determine which of them are right triangles.
(i) a = 7 cm, b = 24 cm and c = 25 cm
Ans. Let
a = 7 cm
b = 24 cm
c = 25 cm
In order to prove that the given sides of a certain triangle forms a right angled triangle we have to prove that square of the larger side is equal to the sum of the squares of the other two sides.
Here, the larger side is c = 25 cm.
Hence, we have to prove that a2 + b2 = c2.
Let solve the left hand side of the above equation.
a2 + b2 = 72 + 242
= 49 + 576
= 625
Now we will solve the right hand side of the equation,
c2 = 252
= 625
Here we can observe that left hand side is equal to the right hand side that is
a2 + b2 = c2.
Therefore, the given sides of a certain triangle form a right angled triangle.
(ii) a = 9 cm, b = 16 cm and c = 18 cm
Ans. Let
a = 9 cm
b = 16 cm
c = 18 cm
In order to prove that the given sides of a certain triangle forms a right angled triangle we have to prove that square of the larger side is equal to the sum of the squares of the other two sides.
Here, the larger side is c = 18 cm.
Hence, we have to prove that a2 + b2 = c2.
Let solve the left hand side of the above equation.
a2 + b2 = 92 + 162
= 81 + 256
= 337
Now we will solve the right hand side of the equation,
c2 = 182
= 324
Here we can observe that left hand side is not equal to the right hand side.
Therefore, the given sides of a certain triangle do not form a right angled triangle.
(iii) a = 1.6 cm, b = 3.8 cm and c = 4 cm
Ans. Let
a = 1.6 cm
b = 3.8 cm
c = 4 cm
In order to prove that the given sides of a certain triangle forms a right angled triangle we have to prove that square of the larger side is equal to the sum of the squares of the other two sides.
Here, the larger side is c = 4 cm.
Hence, we have to prove that a2 + b2 = c2 .
Let solve the left hand side of the above equation.
a2 + b2 = (1.6)2 + (3.8)2
= 2.56 + 14.44
= 17
Now we will solve the right hand side of the equation,
c2 = 42
= 16
Here we can observe that left hand side is not equal to the right hand side.
Therefore, the given sides of a certain triangle do not form a right angled triangle.
(iv) a = 8 cm, b = 10 cm and c = 6 cm
Ans. Let
a = 8 cm
b = 10 cm
c = 6 cm
In order to prove that the given sides of a certain triangle forms a right angled triangle we have to prove that square of the larger side is equal to the sum of the squares of the other two sides.
Here, the larger side is b = 10 cm.
Hence, we have to prove that a2 + b2 = c2.
Let solve the left hand side of the above equation.
a2 + c2 = (8)2 + (6)2
= 64 + 36
= 100
Now we will solve the right hand side of the equation,
b2 = 102
= 100
Here we can observe that left hand side is equal to the right hand side that is
a2 + c2 = b2 .
Therefore, the given sides of a certain triangle form a right angled triangle.
Q.3. A man goes 15 meters due west and then 8 meters due north. How far is he from the starting point?
Ans. Let us draw the diagram. Let A be the starting point. From point B he goes to the north.
Therefore, we obtained the following drawing.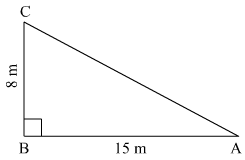 Now we have to find how far is he from the starting point that is we have to find l(AC).
Now we have to find how far is he from the starting point that is we have to find l(AC).
Now we will use Pythagoras theorem to find the length of AC.
AC2 = AB2 + BC2 ………(1)
Let us substituting the values of AB and BC in equation (1) we get,
AC2 = 152 + 82
= 225 + 64
= 289
Let us take the square root we get,
AC = ±√289
AC = ± 17
Since AC is the distance therefore it should be positive.
∴ AC = 17 m
Therefore, he is 17 m from the starting point.
Q.4. A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
Ans. Let us draw the diagram from the given information we get a right angled triangle ABC as shown below,
Let the window be at the point A. We know that angle formed between the building and ground is always 90°.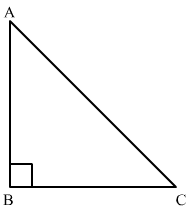 Given: AB = 15 m and CA = 17 m
Given: AB = 15 m and CA = 17 m
Now we will use Pythagoras theorem to find l(BC).
∴ AC2 = AB2 + BC2
Let us substitute the values we get,
∴ 172 = 152 + BC2
∴ 289 = 225 + BC2
Subtracting 225 from both the sides of the equation we get,
∴ 289 - 225 = BC2
∴ 64 = BC2
Let us take the square root we get,
BC = √64
∴ BC = 8
Therefore, the distance of the foot of the ladder from the building is 8m.
Q.5. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
Ans. Let us draw the diagram from the given information.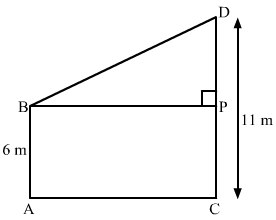 Let us draw a perpendicular from B on CD which meets CD at P.
Let us draw a perpendicular from B on CD which meets CD at P.
It is clear that BP = 12 m because it is given that distance between feet of the two poles is 12 m.
After drawing the perpendicular we get a rectangle BACP such that AB = PC and BP = AC.
Because of this construction we also obtained a right angled triangle BPD.
Now we will use Pythagoras theorem,
BD2 = BP2 + PD2
Let us substitute the values of BP and PD we get,
BD2 = 122 + 52
∴ BD2 = 169
Taking the square root we get, BD = 13
Therefore, distance between the top of the two poles is 13m.
Page No 7.119
Q.6. In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm, Calculate the altitude from A on BC.
Ans. We know that altitude that is a perpendicular drawn on the unequal side of the isosceles triangle bisects that side.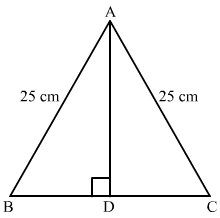 Therefore, BD = DC = 7 cm.
Therefore, BD = DC = 7 cm.
Let us use the Pythagoras theorem in right angled triangle ADB we get,
AB2 = AD2 + BD2
Substituting the values we get,
252 = AD2+ 72
∴ 252 = AD2 + 49
Subtracting 49 from both the sides we get,
625 - 49 = AD2
∴ AD2 = 576
Let us take the square root we get,
AD = 24 cm
Therefore, the altitude of the isosceles triangle is 24 cm.
Q.7. The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Ans. The given information can be represented as follows.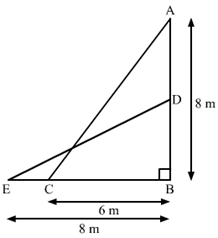
Here, A is the position of the window and AC is the ladder.
Also, DE is the same ladder when it is shifted.
C and E are the original and final position of the foot of the ladder.
Now, applying Pythagoras theorem in ΔABC,
AC2 = AB2 + BC2
⇒ AC2 = (8 m)2 + (6 m)2 = (10 m)2
⇒ AC = 10 m
Now, again applying Pythagoras theorem in ΔEBD
DE2 = EB2 + BD2
⇒ (10 m)2 = (8 m)2 + BD2
⇒ BD2 = 100 m2 − 64 m2 = 36 m2
⇒ BD = 6 m
Thus, the tip of the ladder is now at the height of 6 m above the ground.
Q.8. Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
Ans. Let us draw the diagram from the given information.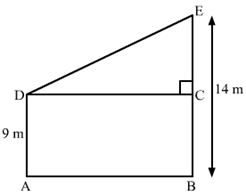 As we are given that distance between their feet is 12 m
As we are given that distance between their feet is 12 m
∴ DC = 12.
Now we get a right angled triangle DCE.
Let us applying the Pythagoras theorem we get,
DE2 = DC2 + EC2
Substituting the values we get,
DE2 = 122 + 52
DE2 = 144 + 25
∴ DE2 = 169
Let us take the square root we get,
∴ DE = 13
Therefore, distance between their top is 13m.
Q.9. Using Pythagoras theorem determine the length of AD in terms of b and c shown in the given figure. Ans. In ∆ABC and ∆DBA,
Ans. In ∆ABC and ∆DBA,
∠A = ∠D (90º each)
∠B = ∠B (Common)
Therefore, by AA-criterion for similarity, we have ∆ABC ∼ ∆DBA.
∴ AB/BD = BC/BA = AC/AD
Now we will substitute the values of AC and AB
∴ c/BD = BC/c = b/AD
We are finding the value of AD therefore; we will use the following ratios,
BC/c = b/AD
Now we will multiple both sides of the equation by 1 / b.
BC/c x 1/b = b/AD x 1/b
We will simplify the above equation as below,
AD = bc/BC ..…(1)
But we know that 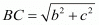 substituting the value of BC in equation (1) we get,
substituting the value of BC in equation (1) we get,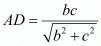
Therefore, the value of AD in terms of b and c is .
.
Q.10. A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Ans.
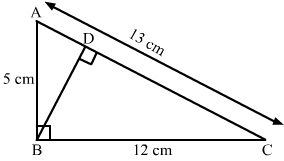 Since BD ⊥ AC we obtained two right angled triangles, ΔABD and ΔBDC.
Since BD ⊥ AC we obtained two right angled triangles, ΔABD and ΔBDC.
In ΔABC and ΔABD
∠A = ∠A (Common angle)
∠B = ∠D
So, by AA-criterion ΔABC ∼ ΔABD
∴ AB/AD = BC/BD = AC/AB
∴ BC/BD = AC / AB
Now we will multiply both sides of the equation by AB x BD.
BC/AB = BD/AC .....(1)
Let us simplify the equation (1) as given below,
BD = BC x AB/AC
Now we will substitute the values of BC, AB and AC.
BD = 12 x 5/13
∴ BD = 60/13
∴ BD = 4.6 cm
Therefore, the length of the altitude is 4.6 cm.
FAQs on Chapter 6 - Triangles, RD Sharma Solutions - (Part - 1) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are the different types of triangles based on their angles? |  |
| 2. How can we determine the area of a triangle using the given side lengths? |  |
| 3. What is the Pythagorean theorem and how is it used in triangles? |  |
| 4. How can we determine the type of triangle based on its side lengths? |  |
| 5. How do we find the perimeter of a triangle? |  |

|
Explore Courses for Class 10 exam
|

|

















