Chapter 6 - Triangles, RD Sharma Solutions - (Part - 3) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 7.120

Q.21. Determine whether the triangle having sides (a − 1) cm, √2a cm and (a + 1) cm is a right angled triangle.
Ans. Let
A = (a - 1)
B = √2a
C = (a + 1)
Larger side is C = (a + 1)
We know that any number plus 1 is always greater than that number minus 1 and product of 2 and its square root.
For example : If a = 36
a - 1 = 35
a + 1 = 37
√2a = 12
If a = 5
a - 1 = 4
a + 1 = 6
√2a = 4.47
In order to prove that the given sides forms a right angled triangle we have to prove that A² + B² = C².
Let us solve the left hand side first.
A² + B² = (a - 1)² + (√2a)²
= a² - 2a + 1 + 4a
= a² + 2a + 1
Now we will simplify the right hand side as shown below,
C² = (a + 1)²
= a² + 2a + 1
We can see that left hand side is equal to right hand side.
Therefore, the given sides determined the right angled triangle.

Q.22. In an acute-angled triangle, express a median in terms of its sides.
Ans. Let ΔABC be acute angled triangle where AD is its median with respect side BC.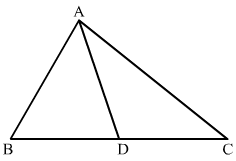

It is known that in any triangle, the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median which bisects the third side.

This is the required expression.

Q.23. In right-angled triangle ABC is which ∠C = 90°, if D is the mid-point of BC, prove that AB² = 4 AD² − 3AC².
Ans. ∆ABC is a right-angled triangle with ∠C = 90°. D is the mid-point of BC.
We need to prove that AB² = 4 AD² − 3AC².
Join AD.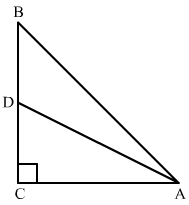

Since D is the midpoint of the side BC, we get
BD = DC
∴ BC = 2 DC
Using Pythagoras theorem in triangles right angled triangle ABC
AB² = AC² − BC²
AB² = AC² − (2DC)²
AB² = AC² − 4DC² .....(1)
Again using Pythagoras theorem in the right angled triangle ADC
AD² = AC² + DC²
DC² = AD² + AC² .....(2)
From (1) and (2), we get
AB² = AC² + 4(AD² - AC²)
AB² = AC² + 4AD² - 4AC²
AB² = AC² + 4AD² - 4AC²
AB² = 4AD² - 3AC²
Hence, AB² = 4AD² - 3AC².

Q.24. In the given figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that :
(i) b² = p² + ax + a²/4
Ans. It is given that D is the midpoint of BC and BC = a.Therefore, BD = DC = a/2 …......(1)
Using Pythagoras theorem in the right angled triangle AED,
AD² = AE² + ED² …......(2)
Let us substitute AD = P, AE = h and AD = x in equation (2), we get P² = h² + x²
Let us take another right angled triangle that is triangle AEC.
Using Pythagoras theorem,
AC² = AE² + EC² …......(3)
Let us substitute  AE = h and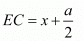in equation (3) we get,
Here we know that DC = a/2 and ED = x.
EC = ED + DC
Substituting AC = b, DC = a/2 and ED = x we get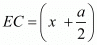

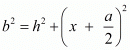
b² = h² + x² + ax + a²/4 …......(4)
From equation (1) we can substitute h² + x² = p² in equation (4),

b² = p² + x² + ax + a²/4 …......(5)

(ii) c² = p² − a^x + a²/4
Ans. Using Pythagoras theorem in right angled triangle AEB,
AB² = AE² + BE² …...... (6)
We know that AB = c and AE = h now we will find BE.
BD = BE + ED
Therefore, BE = BD - ED
We know that BD = a/2 and ED = xsubstituting these values in BE = BD - ED we get,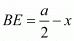
Now we will substitute AB = c, AE = h and  in equation (6) we get,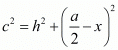

 …......(7)
Let us rewrite the equation (7) as below,
 …......(8)
From equation (1) we can substitute h² + x² = p² in equation (8),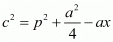

c² = p² - ax + a² / 4 …......(9)

(iii) b² + c² = 2p² + a² / 2
Ans. Now we will add equations (5) and (9) as shown below,

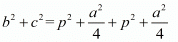
b² + c² = 2p² + a² / 2
Therefore, b² + c² = 2p² + a² / 2.

Q.25. In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that: 
(i) AB ✕ AQ = AC ✕ AP 
(ii) BC² = (AC ✕ CP + AB ✕ BQ)
Ans. Given: ΔABC where ∠BAC is obtuse. PB ⊥AC and QC⊥AB.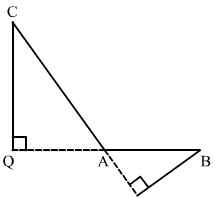

To prove: (i) AB × AQ = AC × AP and (ii) BC² = AC × CP + AB × BQ
Proof: In ΔACQ and ΔABP,
∠CAQ = ∠BAP (Vertically opposite angles)
∠Q = ∠P (= 90°)
∴ ΔACQ ∼ ΔABP [AA similarity test]
⇒ CQ/BP = AC/AB = AQ/AP [Corresponding sides are in the proportion]
AC/AB = AQ/AP
⇒ AQ x AB = AC x AP (1)

In right ΔBCQ,
⇒ BC² = CQ² + QB²
⇒ BC² = CQ² + (QA + AB)²
⇒ BC² = CQ² + QA² + AB² + 2QA × AB
⇒ BC² = AC² + AB² + QA × AB + QA × AB [In right ΔACQ, CQ² + QA² = AC²]
⇒ BC² = AC² + AB² + QA × AB + AC × AP (Using (1))
⇒ BC² = AC (AC + AP) + AB (AB + QA)
⇒ BC² = AC × CP + AB × BQ

Q.26. In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC² = 4(AD² − AC²).
Ans. It is given that ∆ABC is a right-angled at C and D is the mid-point of BC.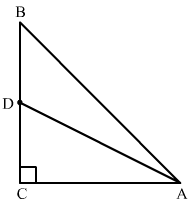

In the right angled triangle ADC, we will use Pythagoras theorem,
AD² = DC² + AC² …......(1)
Since D is the midpoint of BC, we have
DC = BC/2 Substituting DC = BC/2 in equation (1), we get AD² = (BC/2)² + AC²
AD² = (BC/4)² + AC²
4AD² = DC² + 4AC²
BC² = 4AC² + 4AC²
BC² = 4(AD² - AC²)

Q.27. In a quadrilateral ABCD, ∠B = 90°, AD² = AB² + BC² + CD², prove that ∠ACD = 90°.
Ans.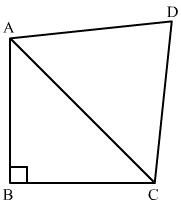
In order to prove angle ∠ACD = 90º it is enough to prove that AD² = AC² + CD².
Given, AD² = AB² + BC² + CD² .....(1)
Since, ∠B = 90º, so applying Pythagoras theorem in the right angled triangle ABC, we get
AC² = AB² + BC² .....(2)
From (1) and (2), we get
AC² = AD² - CD²
AC² + CD² = AD²
Therefore, angle. ∠ACD = 90º (Converse of pythagoras theorem)

Q.28. An aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 x 1 / 2 hours?
Ans. Let us draw the figure first.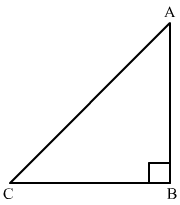
An aeroplane which flies due north at a speed of 1000 km/hr covers the distance AB after 1 x 1 / 2 hr and another aeorplane that flies due west at the speed of 1200 km/hr covers the distance BC after 1 x 1 / 2 hr.
We know that Speed = distance / time
∴ distance = speed x time
Let us calculate AB first as shown below,
AB = 1000 x 1.5
∴ AB = 1500 km
Similarly we can calculate BC.
BC = 1200 x 1.5
∴ BC = 1800 km
Now we have find AC. To find AC we will use Pythagoras theorem,
AC² = AB² + BC²
∴ AC² = (1500)² + (1800)²
∴ AC² = 2250000 + 3240000
∴ AC² = 5490000
Taking square root we get,
AC = 2343.07
Therefore, after 1 x 1 / 2 hrs the aeroplanes will be approximately 2343 km far apart.

Page No 7.122

Q.1. In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
(i) 
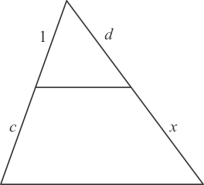(ii)

(iii)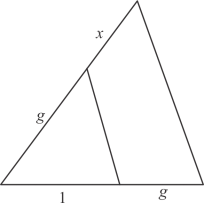 

(iv)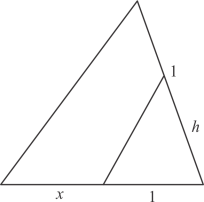 

Ans. In each of the figure, we have to find the value of x
(i)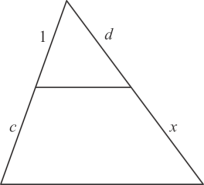 
1 / 1 + c = d / d + x
By cross multiplication on both sides, we get
1 x (d + x) = d x (1 + c
d + x = d + dc
x = d + dc - d

x = dc 
Hence the value of x is dc.
(ii)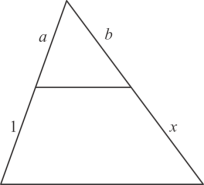
a / a + 1 = b / b + x
By cross multiplication on both sides, we get
a x (b + x) = b x (a + 1)
ab + ax = ab + b
ax = ab + b - ab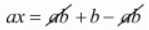

ax = b
x = b / a
Hence the value of x is b / a.