Chapter 7 - Coordinate Geometry, RD Sharma Solutions - (Part-2) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 6.16

Ques.17. Prove that the points (−2, 5), (0, 1) and (2, −3)  are collinear.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula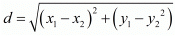

For three points to be collinear the sum of distances between two pairs of points should be equal to the third pair of points.
The given points are A (−2, 5), B (0, 1) and C (2, −3)
Let us find the distances between the possible pairs of points.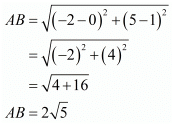

We see that AB + BC = AC
Since sum of distances between two pairs of points equals the distance between the third pair of points the three points must be collinear.
Hence we have proved that the three given points are collinear.

Page No 6.16

Ques.18. The coordinates of the point P are (−3, 2). Find the coordinates of the point Q which lies on the line joining P and origin such that OP = OQ.
Ans. If (x₁,y₁) and (x₂,y₂) are given as two points, then the co-ordinates of the midpoint of the line joining these two points is given as (x_m,y_m) =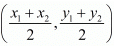
It is given that the point ‘P’ has co-ordinates (−3, 2)
Here we are asked to find out the co-ordinates of point ‘Q’ which lies along the line joining the origin and point ‘P’.Thus we can see that the points ‘P’, ‘Q’ and the origin are collinear.
Let the point ‘Q’ be represented by the point (x, y)
Further it is given that the OP = OQ
This implies that the origin is the midpoint of the line joining the points ‘P’ and ‘Q’.
So we have that (x_m,y_m) = (0,0)
Substituting the values in the earlier mentioned formula we get,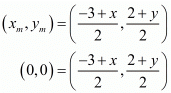

Equating individually we have, x = 3 and y = -2.
Thus the co−ordinates of the point ‘Q’ is (3,-2)

Page No 6.16

Ques.19. Which point on y-axis is equidistant from (2, 3)  and (−4, 1)?
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula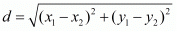

Here we are to find out a point on the y-axis which is equidistant from both the points A (2, 3) and B (−4, 1).
Let this point be denoted as C(x, y).
Since the point lies on the y-axis the value of its ordinate will be 0. Or in other words we have x = 0.
Now let us find out the distances from ‘A’ and ‘B’ to ‘C’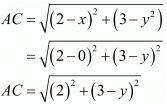


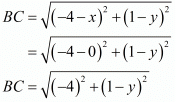
We know that both these distances are the same. So equating both these we get,
AC = BC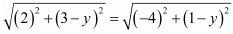

Squaring on both sides we have,

4y = -4
y = -1
Hence the point on the y-axis which lies at equal distances from the mentioned points is (0,-1).

Page No 6.16

Ques.20. The three vertices of a parallelogram are (3, 4) (3, 8) and (9, 8). Find the fourth vertex.
Ans. We are given three vertices of a parallelogram A(3, 4), B(3, 8) and C(9, 8).
We know that diagonals of a parallelogram bisect each other. Let the fourth vertex be D(x, y).
Mid point of BD = ((x+3)/2, (y+8)/2)
Mid point of AC = ((9+3)/2, (4+8)/2) = (6,6)
Since the mid point of BD = mid point of AC
So, ((x+3)/2,(y+8)/2) = (6, 6)
Thus, x = 9, y = 4.
So, the fourth vertex is (9, 4).

Page No 6.16

Ques.21. Find a point which is equidistant from the  points A (−5,4) and B (−1,6) .A -5,4 and B (-1,6) .How many such points are there ?
Ans. Let A(x, y) be the point which is equidistant from the points P(−5, 4) and Q(−1, 6).
Then AP = AQ.
⇒AP² = AQ²
⇒[x−(−5)]²+[y−4]²=[x−(−1)]²+[y−6]²
⇒x² + 25 + 10x + y² + 16 −8y
= x² + 1 + 2x + y² + 36 −12y
⇒10x − 2x − 8y + 12y + 41 − 37 = 0
⇒8x + 4y + 4 = 0
⇒2x+y+1=0  .....(i)
Hence all the points satisfying the equation (i) are equidistant from the points P and Q. There are infinite such points.

Page No 6.16

Ques.22. The centre of a circle is (2a, a−7)2a, a-7). Find the values of a if the circle passes through the point (11,−-9) and has diameter 102–√102 units.
Ans. The length of the diameter is 10√2 units
So, the radius is 5√2 units.
The centre of the circle be C(2a, a−7).
Suppose it passes through the point P(11, −9).
Therefore, PC = r
⇒PC² = r²
⇒(11−2a)² + (−9−a+7)² = (5√2)²
⇒121 + 4a² − 44a + a² + 4 + 4a =50
⇒5a²−40a+75=0
⇒(a−3)(a−5)=0
⇒a=3 or a=5
Hence the values of a are 3 or 5.

Page No 6.16

Ques.23. Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first , from there to his daughter's school and then reaches the office. what is the extra distance travelled by Ayush in reaching the office? (Assume that all distances covered are in straight lines). If the house is situated at (2,4), bank at (5,8), school at (13,14) and office at (13,26) and coordinates are in kilometers.
Ans. The position of the ayush's house is (2,4) and that of the bank is (5,8).
The distance between the house and the bank is


=5 units
The position of the the bank is (5,8) and that of the school is (13,14).
The distance between the bank and the school is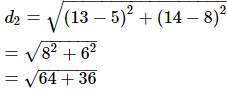

=10 units
The position of the school is (13,14) and that of the office is (13, 6).
The distance between the bank and the school is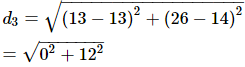

=12 units
Suppose d be the total distance travelled by ayush
d = d₁+d₂+d₃
d = 5+10+12d
= 27 km
Now, let D be the shortest distance between ayush house and the office,
D=

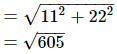
=24.6 km
Thus the extra distance covered by ayush is d − D = 27 − 24.6 = 2.4 km.

Page No 6.16

Ques.24. Find the value of k,if the point P(0, 2) is equidistant from (3, k) and (k, 5).
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula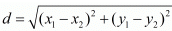

It is said that P(0,2) is equidistant from both A(3,k) and B(k,5).
So, using the distance formula for both these pairs of points we have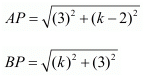 
Now since both these distances are given to be the same, let us equate both.
AP = BP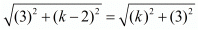

Squaring on both sides we have,
(3)² + (k-2)² = (k)² + (3)²
9 + k² + 4 - 4k = k² + 9
4k = 4
k=1
Hence the value of ‘k’ for which the point ‘P’ is equidistant from the other two given points is k=1.

Page No 6.16

Ques.25. If (−4, 3) and (4, 3)-4, 3 and (4, 3)  are two vertices of an equilateral triangle , find the coordinates of the third vertex , given that the origin lies in the
(i) interior (ii) exterior of the triangle .
Ans. Suppose A(−4, 3) and B(4, 3) be the vertices of an equilateral triangle.
The distance AB is
AB =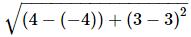= 8 units
Consider the figure below: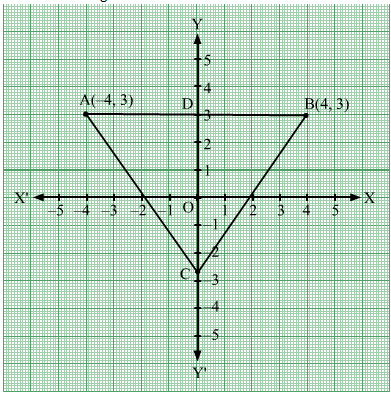

Here, D is point such that CD is perpendicular to AB.
Thus, AD = 4 units.
By pythagoras theorem, we have
AD²+CD² = AC²
⇒4²+CD² = 8²
⇒CD² = 64−16
⇒CD² = 48
⇒CD = 4√3
Since C is on the negative y axis, so coordinate of C are 3−4√3 units.
If C is on the positive y axis, so coordinate of C are 3 + 4√3 units.

Page No 6.16

Ques.26. Show that the points (−3, 2), (−5,−5), (2, −3) and (4, 4) are the vertices of a rhombus. Find the area of this rhombus.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula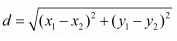

In a rhombus all the sides are equal in length. And the area ‘A’ of a rhombus is given as A = 1/2 (Product of both diagonals)
Here the four points are A(−3,2), B(−5,−5), C(2,−3) and D(4,4)
First let us check if all the four sides are equal.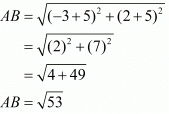



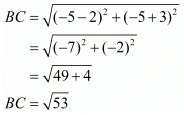
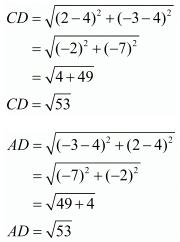
Here, we see that all the sides are equal, so it has to be a rhombus.
Hence we have proved that the quadrilateral formed by the given four vertices is a rhombus.
Now let us find out the lengths of the diagonals of the rhombus.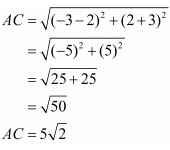

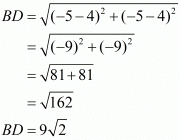
Now using these values in the formula for the area of a rhombus we have,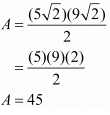

Thus the area of the given rhombus is 45 square units.

Page No 6.16

Ques.27.Find the coordinates of the circumcentre of the triangle whose vertices are (3,0), (−1, −6) and (4,−1). Also, find its circumradius.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula

The circumcentre of a triangle is the point which is equidistant from each of the three vertices of the triangle.
Here the three vertices of the triangle are given to be A(3,0), B(−1,−6) and C(4,−1)
Let the circumcentre of the triangle be represented by the point R(x, y).
So we have AR = BR = CR

Equating the first pair of these equations we have,
AR = BR

Squaring on both sides of the equation we have,
(3-x)² + (-y)² = (-1-x)² + (-6-y²)
9+x²- 6x+y² = 1+x²+2x+36+y²+12y
8x+12y = -28
2x+3y = -7
Equating another pair of the equations we have,
AR = CR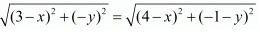

Squaring on both sides of the equation we have,
(3-x)² + (-y)² = (4-x)² + (-1-y²)
9+x²-6x+y² = 16+x²+8x+1+y²+12y
2x+2y=8
x-y=4
Now we have two equations for ‘x’ and ‘y’, which are
2x-3y=-7
x-y=4
From the second equation we have y = -4. Substituting this value of ‘y’ in the first equation we have,
2x+3(x-4)=-7
2x+3x-12=-7
5x=5
x=1
Therefore the value of ‘y’ is,
y=x-4
=1-4
y=-3
Hence the co-ordinates of the circumcentre of the triangle with the given vertices are(1,-3).
The length of the circumradius can be found out substituting the values of ‘x’ and ‘y’ in ‘AR’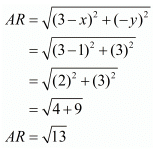

Thus the circumradius of the given triangle is √13units.

Page No 6.16

Ques.28. Find a point on the x-axis which is equidistant from the points (7, 6) and (−3, 4).
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula
Here we are to find out a point on the x−axis which is equidistant from both the points A(7,6) and B(−3,4).
Let this point be denoted as C(x, y).
Since the point lies on the x-axis the value of its ordinate will be 0. Or in other words we have.
Now let us find out the distances from ‘A’ and ‘B’ to ‘C’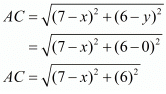


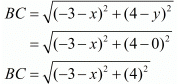
We know that both these distances are the same. So equating both these we get,
AC = BC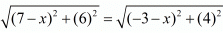

Squaring on both sides we have,
(7-x)² + (6)² = (-3-x)² + (4)²
49+x²-14x+36= 9+x²+6x+16
20x=60
x=3
Hence the point on the x-axis which lies at equal distances from the mentioned points is (3,0).

Page No 6.16:

Ques.29. (i) Show that the points A(5, 6), B(1, 5), C(2, 1) and D(6,2) are the vertices of a square.
(ii) Prove hat the points A (2, 3) B(−2,2) C(−1,−2), and D(3, −1) are the vertices of a square ABCD.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula

In a square all the sides are equal to each other. And also the diagonals are also equal to each other.
Here the four points are A(5,6), B(1,5), C(2,1) and D(6,2).
First let us check if all the four sides are equal.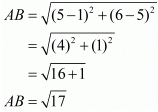



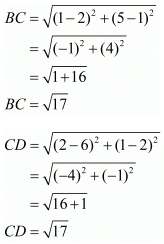
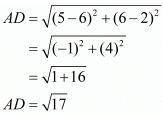
Here, we see that all the sides are equal, so it has to be a rhombus.
Now let us find out the lengths of the diagonals of this rhombus.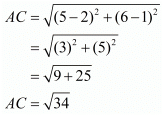


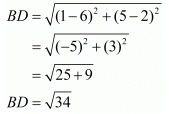
Now since the diagonals of the rhombus are also equal to each other this rhombus has to be a square.
Hence we have proved that the quadrilateral formed by the given four points is a square.

Page No 6.16

Ques.30. Find the point on x-axis which is equidistant from the points (−2, 5) and (2,−3).
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula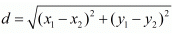

Here we are to find out a point on the x-axis which is equidistant from both the points A(−2,5) and B(2,−3)
Let this point be denoted as C(x, y).
Since the point lies on the x-axis the value of its ordinate will be 0. Or in other words we have y=0.
Now let us find out the distances from ‘A’ and ‘B’ to ‘C’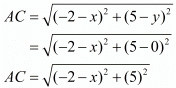


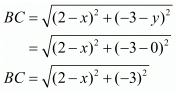
We know that both these distances are the same. So equating both these we get,
AC = BC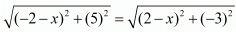

Squaring on both sides we have,
(-2-x²) + (5)² = (2-x)² + (-3)²
4 + x² + 4x + 25 = 4 + x² - 4x + 9
8x = -16
x = -2
Hence the point on the x-axis which lies at equal distances from the mentioned points is (-2,0).