Chapter 7 - Coordinate Geometry, RD Sharma Solutions - (Part-7) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 6.30

Ques.31. Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
Ans. We have two points A (5, 7) and B (3, 9) which form a line segment and similarly C (8, 6) and D (0, 10) form another line segment.
We have to prove that mid-point of AB is also the mid-point of CD.
In general to find the mid-point P(x,y) of two points A(x₁,y₁) and B(x₂,y₂) we use section formula as,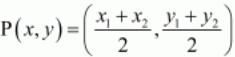

Therefore mid-point P of line segment AB can be written as,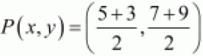

Now equate the individual terms to get,
x=4
y=8
So co-ordinates of P is (4,8)
Similarly mid-point Q of side CD can be written as,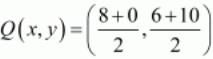

Now equate the individual terms to get,
x=4
y=8
So co-ordinates of Q is (4, 8)
Hence the point P and Q coincides.
Thus mid-point of AB is also the mid-point of CD.

Page No 6.30

Ques.32. Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
Ans. We have to find the distance of a point A (1, 2) from the mid-point of the line segment joining P (6, 8) and Q (2, 4).
In general to find the mid-point P(x,y) of any two points A(x₁,y₁) and B(x₂,y₂) we use section formula as,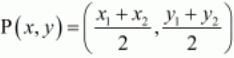

Therefore mid-point B of line segment PQ can be written as,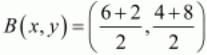

Now equate the individual terms to get,
x=4
y=6
So co-ordinates of B is (4, 6)
Therefore distance between A and B,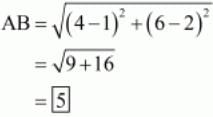

Page No 6.30

Ques.33. If A and B are (1, 4) and (5, 2) respectively, find the coordinates of P when AP/BP = 3/4.
Ans. The co-ordinates of the point dividing two points (x₁,y₁) and (x₂,y₂) in the ratio m:n is given as,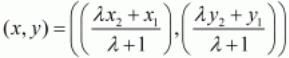
where,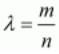
Here the two given points are A(1,4) and B(5,2). Let point P(x, y) divide the line joining ‘AB’ in the ratio 3:4
Substituting these values in the earlier mentioned formula we have,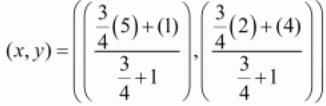


Thus the co-ordinates of the point which divides the given points in the required ratio are.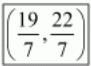

Page No 6.30

Ques.34. Show that the points A (1, 0), B (5, 3), C (2, 7) and D (−2, 4) are the vertices of a parallelogram.
Ans. Let A (1, 0); B (5, 3); C (2, 7) and D (−2, 4) be the vertices of a quadrilateral. We have to prove that the quadrilateral ABCD is a parallelogram.
We should proceed with the fact that if the diagonals of a quadrilateral bisect each other than the quadrilateral is a parallelogram. Now to find the mid-point P(x,y) of two points A(x₁,y₁) and B(x₂,y₂) we use section formula as,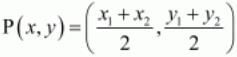
So the mid-point of the diagonal AC is,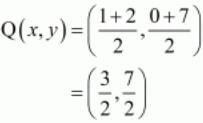

Similarly mid-point of diagonal BD is,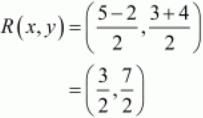

Therefore the mid-points of the diagonals are coinciding and thus diagonal bisects each other. Hence ABCD is a parallelogram.

Page No 6.30

Ques.35. Determine the ratio in which the point P (m, 6) divides the join of A(−4, 3) and B(2, 8). Also, find the value of m.
Ans. The co-ordinates of a point which divided two points (x₁,y₁) and (x₂,y₂) internally in the ratio m:n is given by the formula,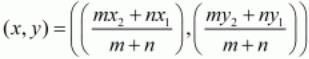

Here we are given that the point P(m,6) divides the line joining the points A(−4,3) and B(2,8) in some ratio.
Let us substitute these values in the earlier mentioned formula.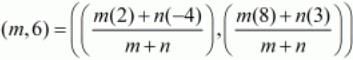

Equating the individual components we have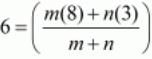

6m+6n=8m+3n
2m=3n
m/n=3/2
We see that the ratio in which the given point divides the line segment is 3:2.
Let us now use this ratio to find out the value of ‘m’.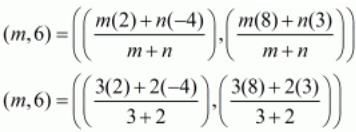

Equating the individual components we have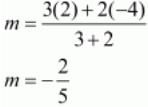

Thus the value of ‘m’ is - (2/5).

Page No 6.30

Ques. 36. Determine the ratio in which the point (−6, a) divides the join of A (−3, 1)  and B (−8, 9). Also find the value of a.
Ans. The co-ordinates of a point which divided two points (x₁,y₁) and (x₂,y₂) internally in the ratio  is given by the formula,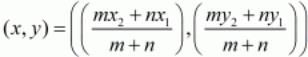

Here we are given that the point P(−6,a) divides the line joining the points A(−3,1) and B(−8,9) in some ratio.
Let us substitute these values in the earlier mentioned formula.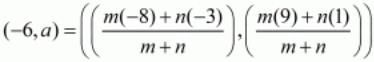

Equating the individual components we have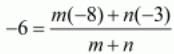

-6m-6n = -8m-3n
2m=3n
m/n=3/2
We see that the ratio in which the given point divides the line segment is 3:2.
Let us now use this ratio to find out the value of ‘a’.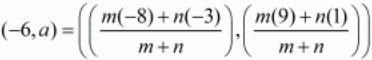


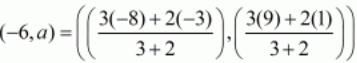
Equating the individual components we have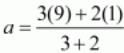

a=29/5.
Thus the value of ‘a’ is 29/5.

Page No 6.30

Ques.37. ABCD is a rectangle formed by joining the points A (−1, −1), B(−1 4) C (5 4) and D (5, −1). P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Ans. We have a rectangle ABCD formed by joining the points A (−1,−1); B (−1, 4); C (5, 4) and D (5,−1). The mid-points of the sides AB, BC, CD and DA are P, Q, R, S respectively.
We have to find that whether PQRS is a square, rectangle or rhombus. In general to find the mid-point P(x,y) of two points A(x₁,y₁) and B(x₂,y₂) we use section formula as,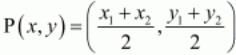

Therefore mid-point P of side AB can be written as,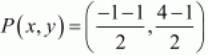

Now equate the individual terms to get,
x=-1
y=-3/2
So co-ordinates of P is (-1,3/2)
Similarly mid-point Q of side BC can be written as,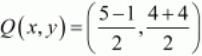

Now equate the individual terms to get,
x=2
y=4
So co-ordinates of Q is (2, 4)
Similarly mid-point R of side CD can be written as,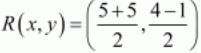

Now equate the individual terms to get,
x=5
y=3/2
So co-ordinates of R is (5,3/2)
Similarly mid-point S of side DA can be written as,
S(x,y)=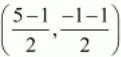
Now equate the individual terms to get,
x=2
y=-1
So co-ordinates of S is (2,−1)
So we should find the lengths of sides of quadrilateral PQRS.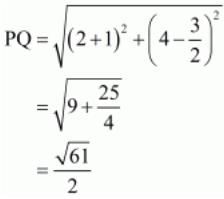




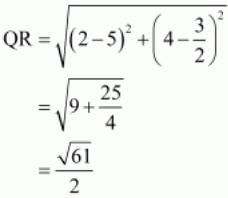
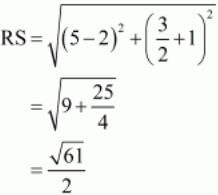
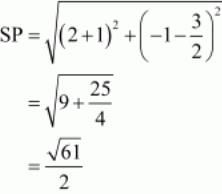
All the sides of quadrilateral are equal.
So now we will check the lengths of the diagonals.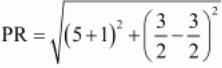
=6
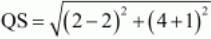=5
All the sides are equal but the diagonals are unequal. Hence ABCD is a rhombus.

Page No 6.30

Ques.38. Points P, Q, R and S divides the line segment joining A(1, 2) and B(6, 7) in 5 equal parts. Find the coordinates of the points P, Q and R.
Ans.

It is given that P, Q, R and S divides the line segment joining A(1, 2) and B(6, 7) in 5 equal parts.
∴ AP = PQ = QR = RS = SB .....(1)
Now,
AP + PQ + QR + RS + SB = AB
⇒ AP + AP + AP + AP + AP = AB [From (1)]
⇒ 5AP = AB
⇒ AP = 1/5AB .....(2)
Now,
PB = PQ + QR + RS + SB = 1/5 AB +1/5 AB + 1/5 AB + 1/5 AB = 4/5 AB .....(3)
From (2) and (3), we get
AP : PB = 1/5 AB : 4/5 AB = 1 : 4
Similarly,
AQ : QB = 2 : 3 and AR : RB = 3 : 2
Using section formula, we get
Coordinates of P =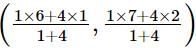= (10/5, 15/5) = (2,3)
Coordinates of Q =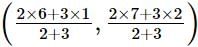= (15/5, 20/5) = (3,4)
Coordinates of R =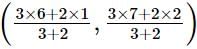= (20/5, 25/5) = (4,5)

Page No 6.30

Ques.39. If A and B are two points having coordinates (−2, −2) and (2, −4) respectively, find the coordinates of P such that AP = 3/7AB.
Ans. We have two points A (−2,−2) and B (2,−4). Let P be any point which divide AB as,
AP = (3/7)AB
Since,
AB=(AP+BP)
So,
Now according to the section formula if any point P divides a line segment joining A(x₁,y₁) and B(x₂,y₂) in the ratio m:n internally than,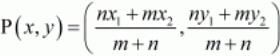

Therefore P divides AB in the ratio 3: 4. So,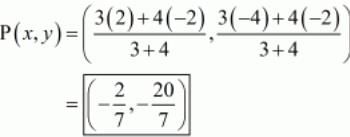

Page No 6.30

Ques.40. Find the coordinates of the points which divide the line segment joining A(−2, 2) and B (2, 8) into four equal parts.
Ans. The co-ordinates of the midpoint (x_m,x_n) between two points (x₁,y₁) and (x₂,y₂) is given by,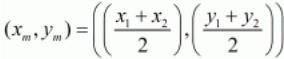

Here we are supposed to find the points which divide the line joining A(−2,2) and B(2,8) into 4 equal parts.
We shall first find the midpoint M(x, y) of these two points since this point will divide the line into two equal parts.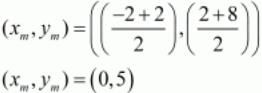

So the point M(0,5) splits this line into two equal parts.
Now, we need to find the midpoint of A(−2,2) and M(0,5) separately and the midpoint of B(2,8) and M(0,5). These two points along with M(0,5) split the line joining the original two points into four equal parts.
Let M₁(e,d) be the midpoint of A(−2,2) and M(0,5).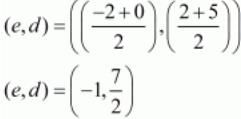

Now let M₂(g,h) bet the midpoint of B(2,8) and M(0,5).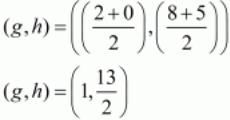

Hence the co-ordinates of the points which divide the line joining the two given points are.

Page No 6.30

Ques.41. Three consecutive vertices of a parallelogram are (−2,−1), (1, 0) and (4, 3). Find the fourth vertex.
Ans. Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (−2,−1); B (1, 0) and C (4, 3). We have to find the co-ordinates of the forth vertex.
Let the forth vertex be D(x,y)
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
Now to find the mid-point P(x,y) of two points A(x₁,y₁) and B(x₂,y₂) we use section formula as,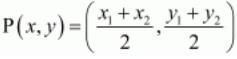

The mid-point of the diagonals of the parallelogram will coincide.
So,
Coordinate of mid-point of AC = Coordinate of mid-point of BD
Therefore,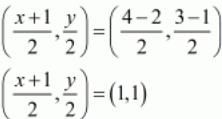

Now equate the individual terms to get the unknown value. So,
x=1
y=2
So the forth vertex is D(1,2) 

Page No 6.30

Ques.42. The points (3, −4) and (−6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (−1,−3). Find the coordinates of the fourth vertex.
Ans. Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (3,−4); B (−1,−3) and C (−6, 2). We have to find the co-ordinates of the forth vertex.
Let the forth vertex be D(x,y)
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
Now to find the mid-point P(x,y) of two points A(x₁,y₁) and B(x₂,y₂) we use section formula as,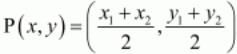

The mid-point of the diagonals of the parallelogram will coincide.
So,
Co-ordinate of mid-point of AC = Co-ordinate of mid-point of BD
Therefore,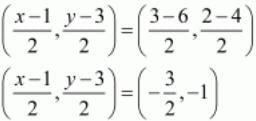

Now equate the individual terms to get the unknown value. So,
x=-2
y=1
So the forth vertex is D(-2,1)

Page No 6.30

Ques.43. If the coordinates of the mid-points of the sides of a triangle are (1, 1) (2, −3) and (3, 4), find the vertices of the triangle.
Ans. The co-ordinates of the midpoint (x_m,x_n) between two points (x₁,y₁) and (x₂,y₂)  is given by,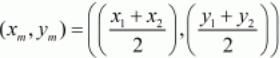

Let the three vertices of the triangle be, A(x₄,y₄),B(x_B,y_B) and C(x_C,y_C).
The three midpoints are given. Let these points be M_AB(1,1),M_BC(2,-3) and M_CA(3,4).
Let us now equate these points using the earlier mentioned formula,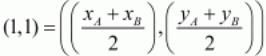

Equating the individual components we get,
x_{A +} x_B = 2
y_A + y_{B = 2}
Using the midpoint of another side we have,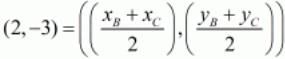

Equating the individual components we get,
x_B + x_C = 4
_yB + y_C = -6
Using the midpoint of the last side we have,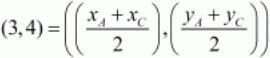

Equating the individual components we get,
x_A + x_C = 6
y_A + y_C = 8
Adding up all the three equations which have variable ‘x’ alone we have,
x_A + x_B + x_B+ x_C + x_A + x_C = 2 + 4 + 6
2(x_A + x_B + x_C) = 12
x_A + x_B + x_C = 6
Substituting x_B + x_C = 4 in the above equation we have,
x_A + x_B + x_C = 6
x_{A + 4 = 6}
x_A = 2
Therefore,
x_A + x_C = 6
x_{C = 6-2}
x_C = 4
And
x_A + x_B = 2
x_{B = 2-2}
x_B = 0
Adding up all the three equations which have variable ‘y’ alone we have,
y_A + y_B + y_B+ y_C + y_A + y_C = 2 - 6 + 8
2(y_A + y_B + y_C) = 4
y_A + y_B + y_C = 2
Substituting y_B + y_C = -6 in the above equation we have,
y_A + y_B + y_C = 2
y_A - 6 = 2
y_A = 8
Therefore,
y_A + y_C = 8
y_C = 8 -8
y_C = 0
And
y_A + y_B = 2
y_B = 2-8
y_B = -6
Therefore the co-ordinates of the three vertices of the triangle are
.

Page No 6.30

Ques. 44. Determine the ratio in which the straight line x − y − 2 = 0 divides the line segment joining (3, −1) and (8, 9).
Ans. Let the line x-y-2=0 divide the line segment joining the points A (3,−1) and B (8, 9) in the ratio λ:1 at any point P(x,y)
Now according to the section formula if point a point P divides a line segment joining A(x₁,y₁) and B(x₂,y₂) in the ratio m:n internally than,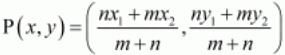

So,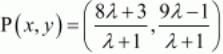

Since, P lies on the given line. So,
x-y-2=0
Put the values of co-ordinates of point P in the equation of line to get,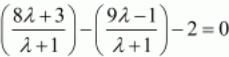

On further simplification we get,
-3λ + 2 =0
So, λ = 2/3
So the line divides the line segment joining A and B in the ratio 2: 3 internally.