Best Study Material for Class 9 Exam
Class 9 Exam > Class 9 Notes > Chapter 8 - Motion
Chapter 8 - Motion - Class 9 PDF Download
| Table of contents |

|
| Motion and Rest |

|
| Speed and Velocity |

|
| Acceleration |

|
| Velocity-Time Equation |

|
| ➢ Derivations of the Three Equations |

|
| Circular Motion |

|
| Summary |

|
Motion and Rest
- An object that changes its position with respect to time is known to be in motion.
- An object is said to be at rest when it does not change its position with respect to time.
- A reference point is required to describe a motion.
- Example:
(i) A car is moving at 60 km/hr. It means that the car is moving with respect to its surrounding. The reference point here is the surrounding. Car is in motion after the light is green whereas it is in rest as the light turns red(ii) A person travelling by bus. The bus and the person are in motion with respect to the surroundings i.e. the plants, trees road, etc. The reference points here are the surroundings.
Car is in motion after the light is green whereas it is in rest as the light turns red(ii) A person travelling by bus. The bus and the person are in motion with respect to the surroundings i.e. the plants, trees road, etc. The reference points here are the surroundings.
But the person and the bus are at rest with each other because they are moving at the same speed and the man always remains at one point inside the bus. The reference point, in this case, is the bus for the man and vice-a-versa.
➢ Motion in a Straight Line
- The point from where an object starts moving is treated as its reference point.
- Distance: The total path length covered by the object from its reference point. Distance only has magnitude (magnitude = numerical value).
- Displacement: The shortest distance covered by an object from its reference point. Displacement has both magnitude and direction.
- The shortest distance is always a straight line dram from the reference point to the point of the end of the motion.
- Example:
Consider an object that moves from point O to C and then comes back to point A. Distance covered by the object = OC + CA
Distance covered by the object = OC + CA
= 60 + 40 = 100 km
Displacement, the shortest distance from the reference point, will be the distance from point O to the endpoint of end of motion i.e. point A, which is OA.
Hence, displacement = OA
➢ Uniform Motion
- An object is said to be in uniform motion when it covers equal distances in equal intervals of times.
Example: A car covered 40 km in each hour. - Graph for Uniform motion
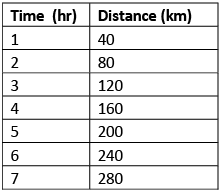
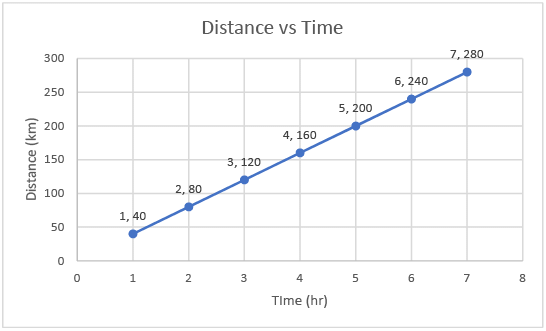 Graph 1: Uniform Motion
Graph 1: Uniform Motion
➢ Non–Uniform Motion
- An object is said to be in non-uniform motion when it covers the unequal distance in equal intervals of time.
Example: A man walking in a park. - Graph of Non-uniform Motion
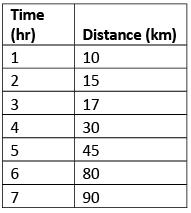
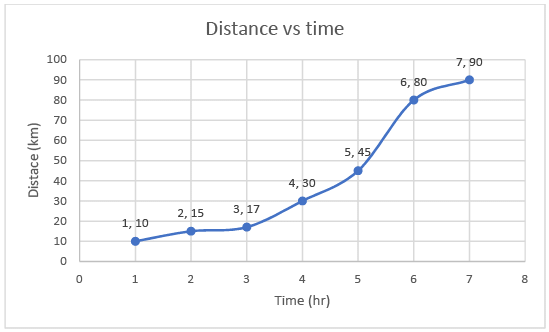 Graph 2: Non-Uniform Motion
Graph 2: Non-Uniform Motion
Speed and Velocity
- Speed: Distance covered per unit time is called speed.
Average speed = Total distance covered / Total time taken i.e. v = s/t
where v = speed, s = distance travelled, t = time taken. - Velocity: Speed with direction is called velocity. Displacement per unit time is called velocity. The direction of velocity is the same as the direction of displacement or motion.
Velocity = Displacement / Total time taken
Average velocity =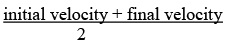 i.e.
i.e. 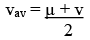
where µ = initial velocity, v = final velocity.
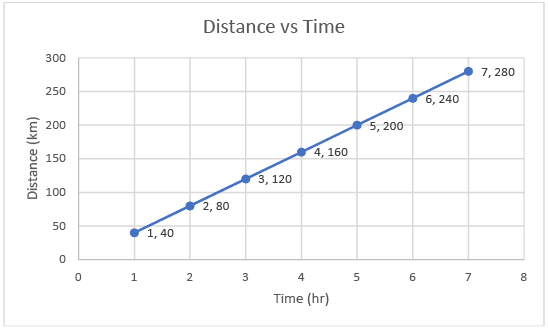 Graph 3 - Distance vs Time at a constant velocity
Graph 3 - Distance vs Time at a constant velocity
Question for Chapter 8 - Motion
Try yourself:Which of the following statement is correct regarding velocity and speed of a moving body?
View Solution
Acceleration
- The rate of change of velocity is known as acceleration.
Acceleration = Change in velocity / Time taken i.e.
where v = final velocity, µ = initial velocity, t = time taken. - Graph
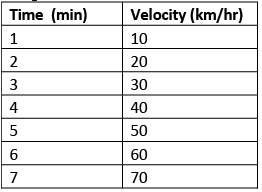
 Graph 4 - Velocity vs Time at uniform acceleration
Graph 4 - Velocity vs Time at uniform acceleration - The area under two points in a velocity-time graph gives the distance covered in that time.
- The distance between time interval D (3hr) and C (5hr) is given by the area of the trapezium ABCD, i.e.
Area of trapezium = (1/2) (b1 + b2) * h = (1/2) (AD + BC) * h
= (1/2) * (30 + 50) * 2 (height = 5 – 3 (time period))
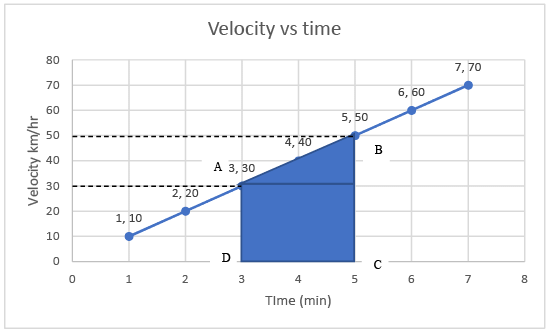
= (1/2) * (80) * 2 = 80 km - But if the object moves with constant velocity and there is no acceleration, then velocity will be the same at all times.
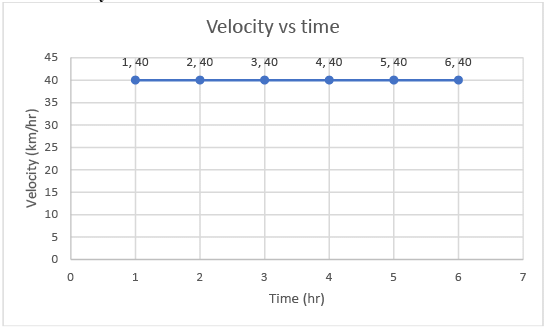 Velocity vs time graph at zero acceleration
Velocity vs time graph at zero acceleration
Question for Chapter 8 - Motion
Try yourself:A car of mass 1000 kg is moving with a velocity of 10 m/s. If the velocity-time graph for this car is a horizontal line parallel to the time axis, then the velocity of the car at the end of 25 s will be:
View Solution
 |
Download the notes
Chapter 8 - Motion
|
Download as PDF |
Download as PDF
Velocity-Time Equation
- v = u + at
- s = ut + (1/2) at2
- 2as = v2 – u2
➢ Derivations of the Three Equations
(a) v = u + at
- Consider an object moving at a uniform acceleration and forms the following graph as AB.
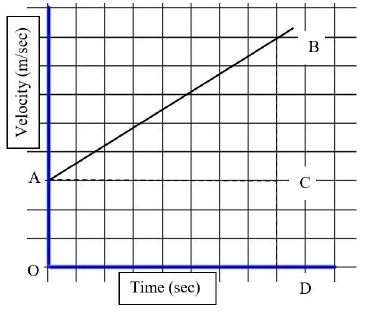 In the above graph:
In the above graph:
CD = Initial velocity = u, BD = Final Velocity = v, and OD = time = t
∵ BD = BC + CD
⇒ BC = BD – CD = v – u
∵ Acceleration = Change in velocity / Time taken
⇒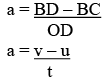
∴ at = v – u
i.e. u + at = v or v = u + at
Hence, proved or the first equation derived. - Deriving the above equation without the help graph
Let, Change in velocity = Final velocity(v) – Initial velocity (u)
Time taken = t and Acceleration = a
∵ Acceleration = Change in velocity / Time taken
∴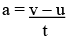
i.e. at = v – u or v = u + at
Hence, proved or first equation derived.
(b) s = ut + 1 / 2at2
- Consider an object moving at a uniform acceleration and forms the following graph as AB.
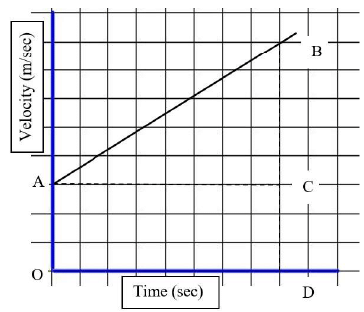 In the above graph:
In the above graph:
The distance travelled in a velocity vs time graph is the area under two points.
► Distance travelled in the above graph between point A and B = Area of trapezium AODB
► s = Area of trapezium AODB = Area of rectangle AOCB + Area of triangle ACB
► s = OD * CD + (1/2) * AC * CB...(i)
► OD = time taken or ‘t’, CD = Initial velocity or ‘u’, AC = OD = time taken or ‘t’
► CB = DB – CD = (v – u)
We know that: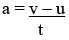 i.e. v – u = at
i.e. v – u = at
∴ CB = at
Putting the values of OD, CD, AC, and CB in equation (i)
⇒ s = t * u + (1/2) * t * at
⇒ s = ut + (1/2) at2
Hence, proved or derived second equation. - Deriving the above equation without the help graph
Average velocity = Total Distance covered / Time taken
i.e.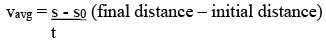
⇒ s = vavg * t...(i)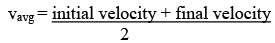
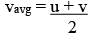
Putting the value of Vavg in equation (i)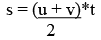 ...(ii)
...(ii)
We also know that: v = u + at
Putting the value of v in equation (ii)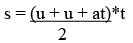
⇒ s = ut + 1 / 2at2
Hence, proved or derived the second equation.
(c) 2as = v2 – u2
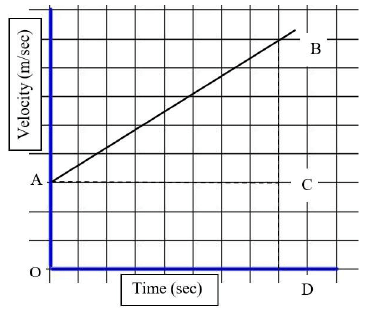
- Consider an object moving at a uniform acceleration and forms the following graph as AB.
 In the above graph:
In the above graph:
The distance travelled in a velocity vs time graph is the area under two points.
Distance (s) travelled in the above graph between point A and B = Area of trapezium AODB
⇒ s = Area of trapezium AODB = (1/2) * (b1 + b2) * h
⇒ s = (1/2) * (b1 + b2) * h...(i)
From the graph: b1 = AO or ‘u’, b2 = DB or ‘v’ and ‘h’ = OD or ‘t’
Putting these values in equation (i)
⇒ s = (1/2) (AO + DB) * OD
⇒ 2s = (u + v) * t ...(ii)
We also know that: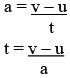
Putting the value of ‘t’ in equation (ii)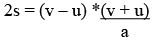
⇒ 2as = v2 – u2
Hence, proved or derived the third equation.
Circular Motion
- An object is said to be in a circular motion when it rotates around a center, in a circle of radius ‘r’.
 The wheels on the bicycle are in a circular motion
The wheels on the bicycle are in a circular motion - Distance covered by the object in one round = circumference of the circle = 2πr
- Speed = Distance / time = 2πr / t
- However, the displacement in a circular motion is zero as the object returns at its initial or reference point after one rotation.
Question for Chapter 8 - Motion
Try yourself:A particle is moving in a circular path of radius r.
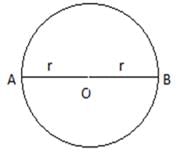
The displacement after half a circle would be:

The displacement after half a circle would be:
View Solution
Summary
- Distance: The total path length covered by the object from its reference point.
- Displacement: The shortest distance covered by an object from its reference point. Displacement has both magnitude and direction.

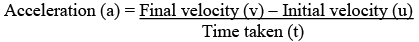
- Equations of motions
(i) v = u + at
(ii) s = ut + 1 / 2at2
(iii) 2as = v2 – u2
Question for Chapter 8 - Motion
Try yourself:Which of the following can sometimes be ‘zero’ for a moving body?
i. Average velocity
ii. Distance travelled
iii. Average speed
iv. Displacement
View Solution
FAQs on Chapter 8 - Motion - Class 9
| 1. What is the difference between speed and velocity? |  |
| 2. How is acceleration calculated? |  |
Ans. Acceleration is calculated by dividing the change in velocity by the time taken for that change to occur. The formula for acceleration is given by a = (v - u) / t, where 'a' represents acceleration, 'v' represents final velocity, 'u' represents initial velocity, and 't' represents time.
| 3. What is the velocity-time equation? |  |
Ans. The velocity-time equation is a formula used to calculate the final velocity of an object when its initial velocity, acceleration, and time are known. The equation is given by v = u + at, where 'v' represents final velocity, 'u' represents initial velocity, 'a' represents acceleration, and 't' represents time.
| 4. How can the three equations of motion be derived? |  |
Ans. The three equations of motion can be derived by using calculus and integrating the equation for acceleration with respect to time. By integrating, we can find the equations for velocity and displacement as a function of time, which result in the three equations of motion.
| 5. What is circular motion? |  |
Ans. Circular motion refers to the movement of an object along a circular path. In circular motion, the object continuously changes its direction, but its speed may remain constant. Examples of circular motion include the motion of a car around a roundabout or the motion of a planet around the sun.
Download as PDF
Top Courses for Class 9
Related Searches





















