Algebraic Expressions Chapter Notes | Mathematics Class 7 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Constants and Variables |

|
| Terms |

|
| Algebraic Expressions |

|
| Addition |

|
| Subtraction |

|
| Multiplication |

|
| Division |

|
| Value of an Algebraic Expression |

|
Introduction
Imagine a world where numbers and letters team up to solve real-life puzzles! That's what algebraic expressions are all about. In this exciting chapter, we dive into the fascinating branch of mathematics called Algebra, where we use numbers, operations, and letters to represent quantities that can change. Whether it's calculating the cost of pens or finding the perimeter of a rectangle, algebraic expressions help us generalize and simplify arithmetic. Get ready to explore constants, variables, terms, and how to add, subtract, multiply, and divide these expressions to unlock the magic of Algebra!
Constants and Variables
- Constants: Numbers with a fixed value.
- Variables: Letters representing numbers that can change.
Stepwise Explanation:
- Constants are numbers like 3, -4, or 11(1/6) that always stay the same.
- Variables, also called literals, are letters like x, y, or z that stand for unknown or changing values.
- Combinations of constants (e.g., 2 + 3 = 5) result in a constant.
- Combinations of variables (e.g., x + y) or constants and variables (e.g., 2x) are variables.
- All arithmetic rules (addition, subtraction, multiplication, division) apply to variables.
Example: Rahul wants to buy pens costing ₹15 each. For 'n' pens, the total cost is 15n. Here, 15 is a constant, and n is a variable.
Terms
Definition: A term is a constant, variable, or a combination of both connected by multiplication or division.
Types of Terms:
- Constant Term: A term without variables (e.g., 6).
- Numerical Factor: The constant part in a term (e.g., 8 in 8ab).
- Literal Factors: The variable parts in a term (e.g., a, b in 8ab).
Stepwise Explanation:
- Terms can be single numbers (e.g., 6), variables (e.g., x), or products/divisions like 13ab or 8a/xy.
- In a term like 8ab, 8 is the numerical factor, and a, b, or ab are literal factors.
- Terms are classified as like or unlike based on their literal factors.
Example: In the term 8ab, 8 is the numerical factor, and a, b, and ab are literal factors.
Like Terms
Definition: Terms with the same literal factors.
Stepwise Explanation:
- Like terms have identical variables with the same powers.
- Only their numerical coefficients differ.
- Like terms can be combined by adding or subtracting their coefficients.
Example: 8ab and -11ab are like terms because they share the same literal factors (ab).
Unlike Term
Definition: Terms with different literal factors.
Stepwise Explanation:
- Unlike terms have different variables or different powers of the same variables.
- They cannot be combined into a single term.
Example: xy and 2x are unlike terms because their literal factors (xy and x) are different.
Coefficient
Definition: A factor of a term is a coefficient of the product of the remaining factors.
Types:
- Numerical Coefficient: The constant factor in a term.
- Literal Coefficient: The variable factor(s) in a term.
Stepwise Explanation:
- In a term, any factor can be considered a coefficient of the rest of the term.
- For example, in p2q, p2 is the coefficient of q, and q is the coefficient of p2.
- Numerical coefficients are constants, while literal coefficients involve variables.
Example: In the term -3a2p, the coefficient of -3 is a2p, and the coefficient of a2 is -3p.
Algebraic Expressions
Definition: A combination of one or more terms connected by addition or subtraction.
Stepwise Explanation:
- Algebraic expressions combine constants and variables using + or -.
- They cannot be evaluated without knowing the values of the variables.
- To form an expression, translate words into symbols (e.g., "three times m plus 6" becomes 3m + 6).
Example: The statement "three times m increased by 6 equals 40" is written as 3m + 6 = 40.
Monomial
- Definition: An expression with one term and non-negative integer powers of variables.
Stepwise Explanation:
- A monomial has only one term, like p or 2xy.
- The powers of variables must be whole numbers (0, 1, 2, ...).
Example: p, 2xy, and -3/4 x2 are monomials.
Binomial
Definition: An expression with two terms and non-negative integer powers of variables.
Stepwise Explanation:
- A binomial consists of two terms connected by + or -.
- Each term must have non-negative integer powers.
Example: a + b and -3x4 + y2/2 are binomials.
Trinomial
Definition: An expression with three terms and non-negative integer powers of variables.
Stepwise Explanation:
- A trinomial has three terms connected by + or -.
- Each term must have non-negative integer powers.
Example: x + z2 + yz is a trinomial.
Polynomial in One Variable
Definition: An expression with non-negative integer powers of one variable and a finite number of terms.
Stepwise Explanation:
- The variable (e.g., x) has whole number powers (0, 1, 2, ...).
- The degree is the highest power of the variable.
- A constant polynomial (e.g., 10) has degree 0.
- Terms like 1/x or 1/x2 are not allowed.
Example: -8a3 + 5a - 5/3 is a polynomial in a with degree 3.
Polynomial in Two or More Variables
Definition: An expression with non-negative integer powers of two or more variables.
Stepwise Explanation:
- Each term’s degree is the sum of the powers of all variables in that term.
- The polynomial’s degree is the highest sum among all terms.
Example: For 3x2y + 5y2 - 7xy + 8x, the degrees of terms are 3, 2, 2, and 1, respectively. The polynomial’s degree is 3.
Addition
Addition of Like Terms
Definition: Adding like terms results in a term with the same literal factors and a numerical coefficient equal to the sum of the coefficients.
Stepwise Explanation:
- Identify like terms (same literal factors).
- Add their numerical coefficients.
- Keep the literal factors unchanged.
Example: 4x + 9x = (4 + 9)x = 13x.
Addition of Unlike Terms
Definition: Unlike terms cannot be combined into a single term and are written with a + sign.
Stepwise Explanation:
- Unlike terms have different literal factors.
- Write them as separate terms with a + sign.
Example: 3ab + 2pq remains 3ab + 2pq.
Addition of Polynomials
Definition: Combine like terms of polynomials using horizontal or column methods.
Stepwise Explanation:
- Horizontal Method: Group like terms and add their coefficients.
- Column Method: Align like terms vertically and add column-wise.
- Retain unlike terms as they are.
Example:
Add 2x + 4y - 3z, 5y + 2z, and -6x - 9y + 3z:
(2x + 4y - 3z) + (5y + 2z) + (-6x - 9y + 3z) = (2 - 6)x + (4 + 5 - 9)y + (-3 + 2 + 3)z = -4x + 2z.
Subtraction
Subtraction of Like Terms
Definition: Subtracting like terms results in a term with the same literal factors and a numerical coefficient equal to the difference of the coefficients.
Stepwise Explanation:
- Identify like terms.
- Subtract their numerical coefficients.
- Keep the literal factors unchanged.
Example: 3x - 5x = (3 - 5)x = -2x.
Subtraction of Unlike Terms
Definition: Unlike terms cannot be combined and are written with a - sign.
Stepwise Explanation:
- Unlike terms have different literal factors.
- Write them as separate terms with a - sign.
Example: 9xy - 5a2 remains 9xy - 5a2.
Subtraction of Polynomials
Definition: Subtract polynomials by changing the signs of the terms in the polynomial being subtracted and combining like terms.
Stepwise Explanation:
- Horizontal Method: Change the sign of each term in the polynomial being subtracted, then combine like terms.
- Column Method: Align like terms vertically, change the signs of the lower polynomial, and add column-wise.
Example: Subtract 9pq + 7p2 - 8q2 from 12p2 - 15q2 + 8p:
(12p2 - 15q2 + 8p) - (9pq + 7p2 - 8q2) = 12p2 - 15q2 + 8p - 9pq - 7p2 + 8q2
= 5p2 - 7q2 + 8p - 9pq.
Multiplication
Definition: Multiplication of variables follows specific properties.
Stepwise Explanation:
- Variables multiply as ab = ba (commutative property).
- a(bc) = (ab)c (associative property).
- a × 0 = 0.
- a × 1 = a.
- a × (b + c) = ab + ac (distributive property).
- For variables with exponents, xm × xn = xm+n.
Example: (x2 + y2) × (x + y) = x2(x + y) + y2(x + y) = x3 + x2y + xy2 + y3.
Multiplication of Monomials
Definition: The product of monomials is a monomial with the product of numerical coefficients Hosts and the product of literal coefficients.
Stepwise Explanation:
- Multiply the numerical coefficients.
- Multiply the literal coefficients using exponent rules.
- Combine to form a single monomial.
Example: 5x × 4y = (5 × 4) × (x × y) = 20xy.
Multiplication of a Polynomial and a Monomial
Definition: Multiply each term of the polynomial by the monomial and add the products.
Stepwise Explanation:
- Distribute the monomial to each term of the polynomial.
- Multiply the numerical and literal coefficients separately.
- Add the resulting terms, combining like terms if necessary.
Example: (6ab) × (3y - 2xz + z2) = 18aby - 12abxz + 6abz2.
Multiplication of Two Polynomials
Definition: Multiply each term of one polynomial by each term of the other and add the products.
Stepwise Explanation:
- Use the distributive property to multiply each term of the first polynomial by each term of the second.
- Add the products, combining like terms.
- Alternatively, use the column method by aligning like terms and adding.
Example: (x + y) × (x - y + 3) = x(x - y + 3) + y(x - y + 3) = x2 - xy + 3x + xy - y2 + 3y = x2 - y2 + 3x + 3y.
Division
Definition: Division of variables follows exponent rules.
Stepwise Explanation:
- For xm ÷ xn, subtract exponents: xm-n if m > n, or 1/xn-m if m < n.
Example: 20x3y5 ÷ 4xy4 = (20/4) × (x3-1) × (y5-4) = 5x2y.
Division of a Monomial by a Monomial
Definition: Divide the numerical and literal coefficients separately.
Stepwise Explanation:
- Write the dividend over the divisor as a fraction.
- Simplify the numerical coefficients.
- Apply exponent rules to the literal coefficients.
Example: 20x3y5 ÷ 4xy4 = 5x2y.
Division of a Polynomial by a Monomial
Definition division of each term of the polynomial by the monomial and adding the quotients.
Example:
(3ab + 15a2b - 12ab3) ÷ (-3ab2) = -1/b - 5a/b + 4b.
Stepwise Explanation:
- Divide each term of the polynomial by the monomial.
- Simplify the numerical and literal coefficients.
- Add the resulting terms.
Division of a Polynomial by a Polynomial
Definition: Use long division to divide polynomials.
Stepwise Explanation:
- Arrange dividend and divisor in descending order of powers.
- Divide the first term of the dividend by the first term of the divisor to get the first quotient term.
- Multiply the quotient term by the divisor and subtract from the dividend.
- Repeat with the new dividend until the remainder is zero or has a lower degree than the divisor.
- Verify using: Dividend = Divisor × Quotient + Remainder.
Example: Divide x2 + 10x - 75 by x - 5: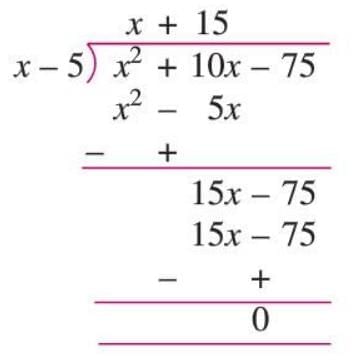 Quotient = x + 15, Remainder = 0.
Quotient = x + 15, Remainder = 0.
Verification: (x - 5)(x + 15) = x2 + 10x - 75.
Value of an Algebraic Expression
Definition: The value of an expression is found by substituting given values for the variables.
Stepwise Explanation:
- Replace each variable with its given value.
- Perform the operations in the correct order (parentheses, exponents, multiplication/division, addition/subtraction).
- Simplify to find the final value.
Example: Find the value of 3m2 - 2m + 7 when m = 2:
3(2)2 - 2(2) + 7 = 3(4) - 4 + 7 = 12 - 4 + 7 = 15.
|
47 videos|118 docs|23 tests
|
FAQs on Algebraic Expressions Chapter Notes - Mathematics Class 7 ICSE
| 1. What are constants and variables in algebraic expressions? |  |
| 2. How do you perform addition with algebraic expressions? |  |
| 3. What is the difference between subtraction and addition of algebraic expressions? |  |
| 4. How is multiplication performed in algebraic expressions? |  |
| 5. How do you find the value of an algebraic expression? |  |




















