Circles Class 10 Notes Maths Chapter 10
| Table of contents |

|
| Introduction to Circles |

|
| Tangent to a Circle |

|
| Number of Tangents from a Point on a Circle |

|
| Summary |

|
Introduction to Circles
Circle: It is a closed two-dimensional geometrical figure, such that all points on the surface of a circle are equidistant from the point called the “centre”.
A circle is a locus of a point that moves in such a way that the distance from that point is always fixed.
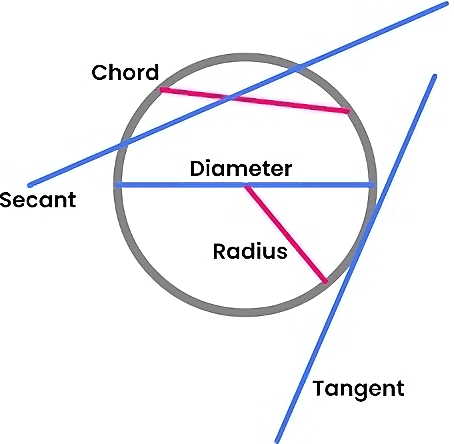 Parts of a Circle
Parts of a Circle
- Radius: The constant distance from the centre to the circumference (boundary) of the circle.
- Secant: A secant is a line that crosses a curve at two or more separate locations. A secant intersects a circle at exactly two locations in the case of a circle. In the figure, the line FG intersects the circle at two points P and Q. FG is the secant of the circle.
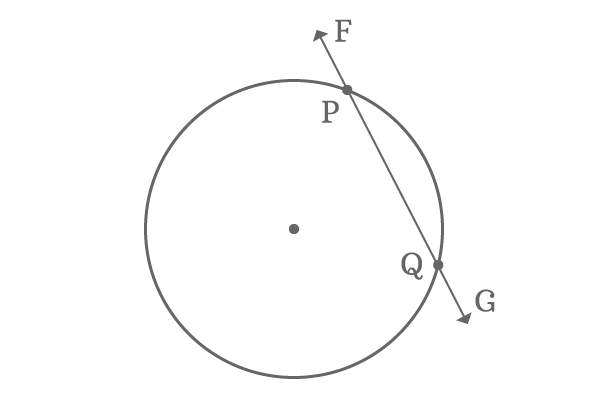 Secant
Secant - Chord: Any line segment joining the two points on the circumference of the circle. In the above figure, PQ is a chord.
- Diameter: The longest distance between the two points on the circumference of the circle. It is the longest chord.
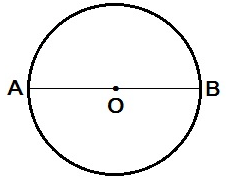 Here, AO is the radius of the circle and AB is the diameter of the circle.
Here, AO is the radius of the circle and AB is the diameter of the circle.
- Tangent: A tangent to a circle is a line that touches the circle at exactly one point. For every point on the circle, there is a unique tangent passing through it.
 Tangent of a Circle
Tangent of a Circle Non-intersecting lines: These are made up of two or more lines that do not intersect. The circle and the line AB have no common point.
- Lines that do not intersect can never meet.
- The parallel lines are another name for them.
- They stay at the same distance from one another at all times.
Tangent to a Circle
A tangent to a circle is a line that intersects the circle at only one point.
(i) There is only one tangent at a point of the circle.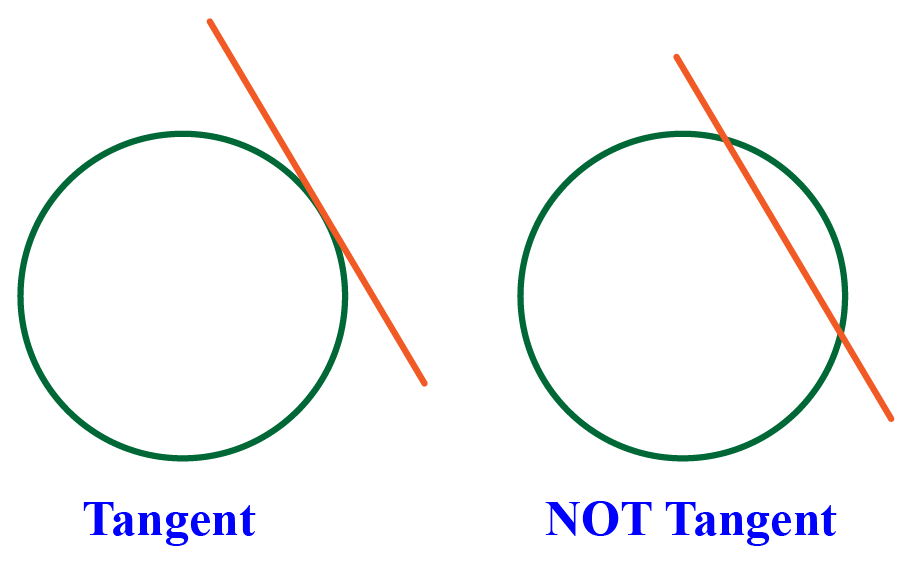
(ii) The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide.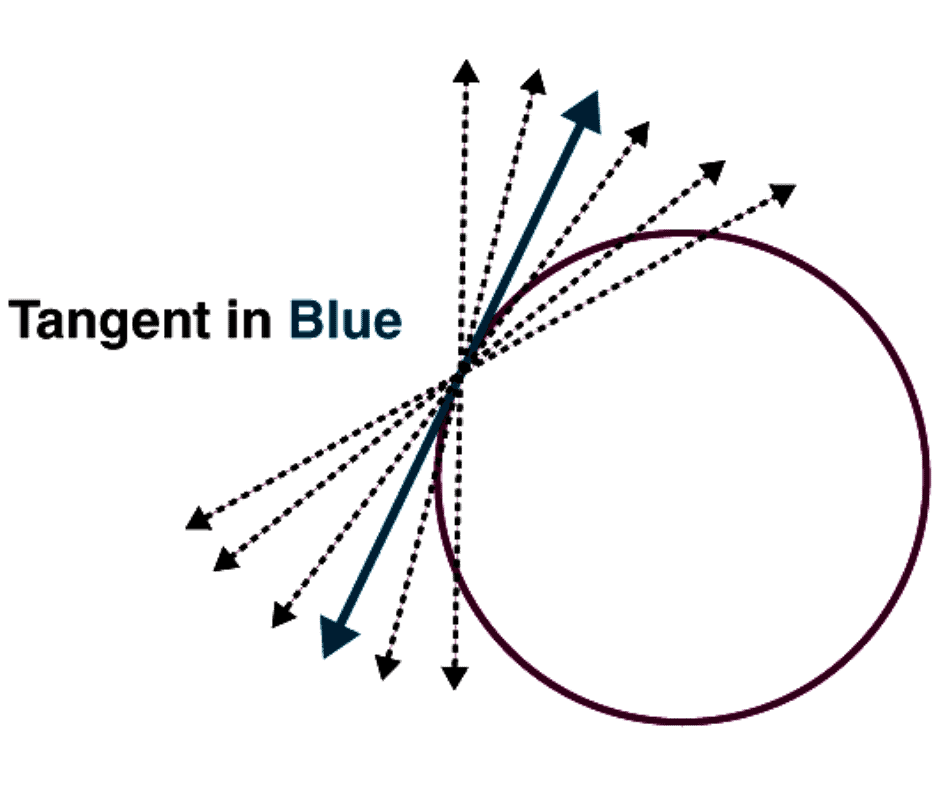 (iii) The common point of the tangent and the circle is called the point of contact and the tangent is said to touch the circle at that point.
(iii) The common point of the tangent and the circle is called the point of contact and the tangent is said to touch the circle at that point.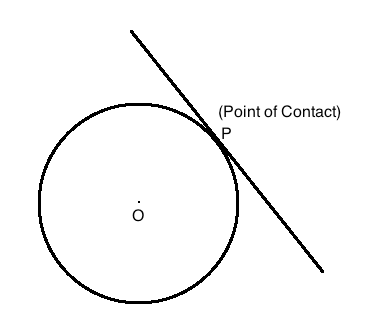
Theorem 1
The theorem states that “the tangent to the circle at any point is perpendicular to the radius of the circle that passes through the point of contact”.
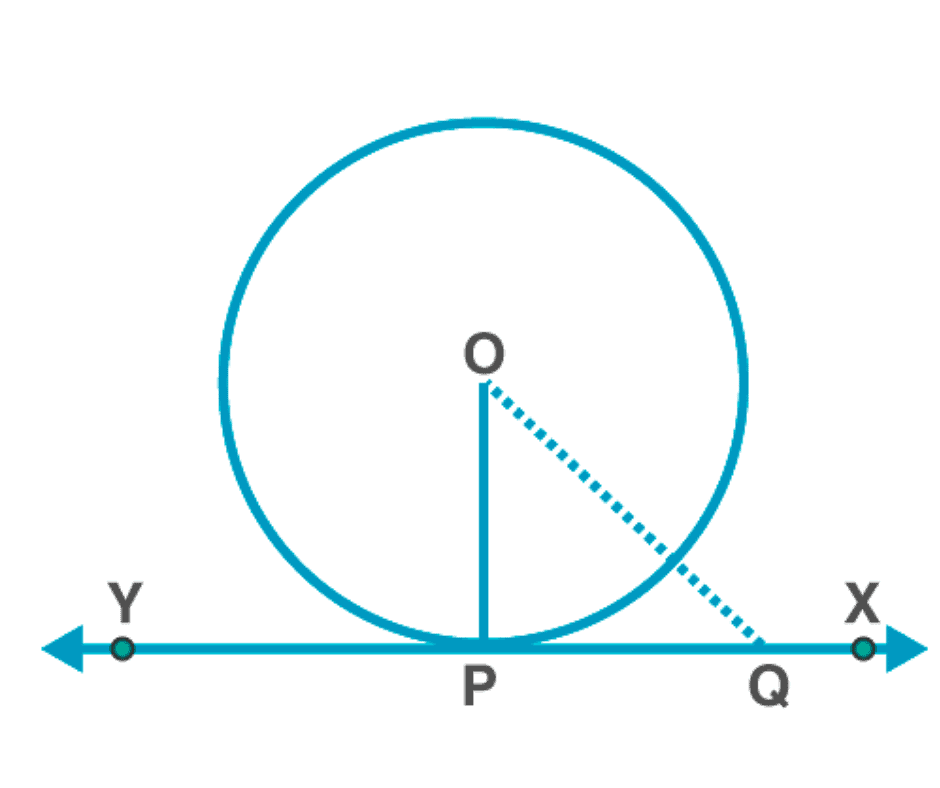
According to the theorem, O is the centre and OP⊥XY.
Proof: Let Q be a point on XY.
Connect OQ.
Suppose it touches the circle at R.
Hence,
OQ > OR
OQ > OP (as OP = OR, radius).
The same will be the case for all other points on the circle.
Hence, OP is the smallest line that connects XY.
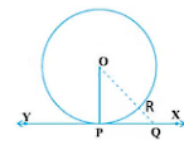
Thus, OP is the smallest line that connects XY, and the smallest line is perpendicular.
∴ OP ⊥ XY
Note:
1. By the theorem above, we can also conclude that at any point on a circle, there can be one and only one tangent.
2. The line containing the radius through the point of contact is also sometimes called the ‘normal’ to the circle at the point.
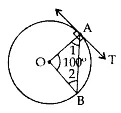
Example 1: In the given figure, O is the centre of a circle, AB is a chord and AT is the tangent at A. If ∠AOB = 100°, then calculate ∠BAT.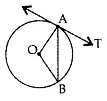
Solution:
∠1 = ∠2
∠1 + ∠2 + 100° = 180°
∠1 + ∠1 = 80° (∠1 =∠2, isoceles triangle formed by radius)
⇒ 2∠1 = 80°
⇒ ∠1 = 40°
∠1 + ∠BAT = 90° (the tangent to the circle at any point is perpendicular to the radius of the circle)
∠BAT = 90° – 40° = 50°
Number of Tangents from a Point on a Circle
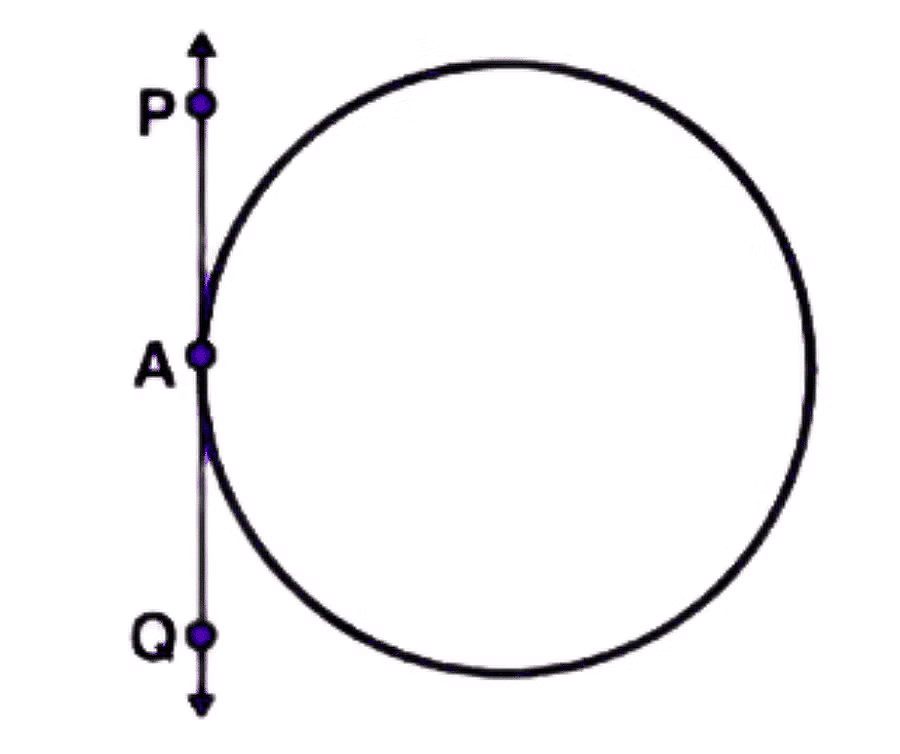
1. There is no tangent to a circle passing through a point lying inside the circle.
If a point lies inside a circle, any line passing through that point will intersect the circle at two points and is called a secant. Therefore, it is not possible to draw a tangent to a circle that passes through a point inside the circle.
2. There is one and only one tangent to a circle passing through a point lying on the circle.
When a point lies on the circle, there is exactly one tangent to a circle that passes through it.
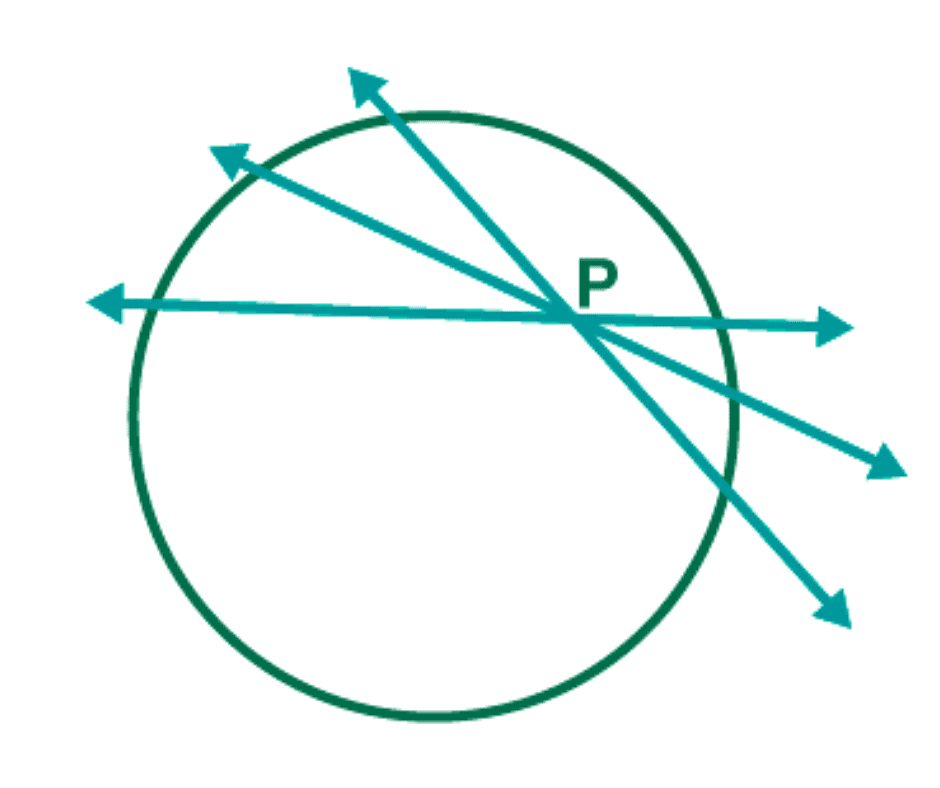
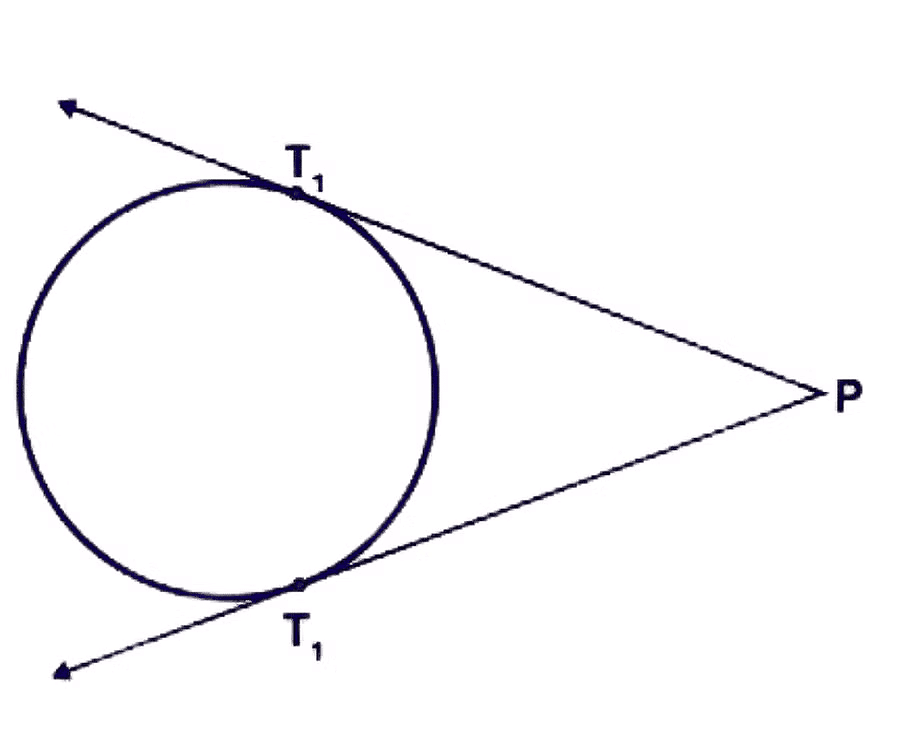
3. There are exactly two tangents to a circle through a point lying outside the circle
If a point is located outside of a circle, then there exist exactly two tangents that can be drawn to the circle passing through the point.
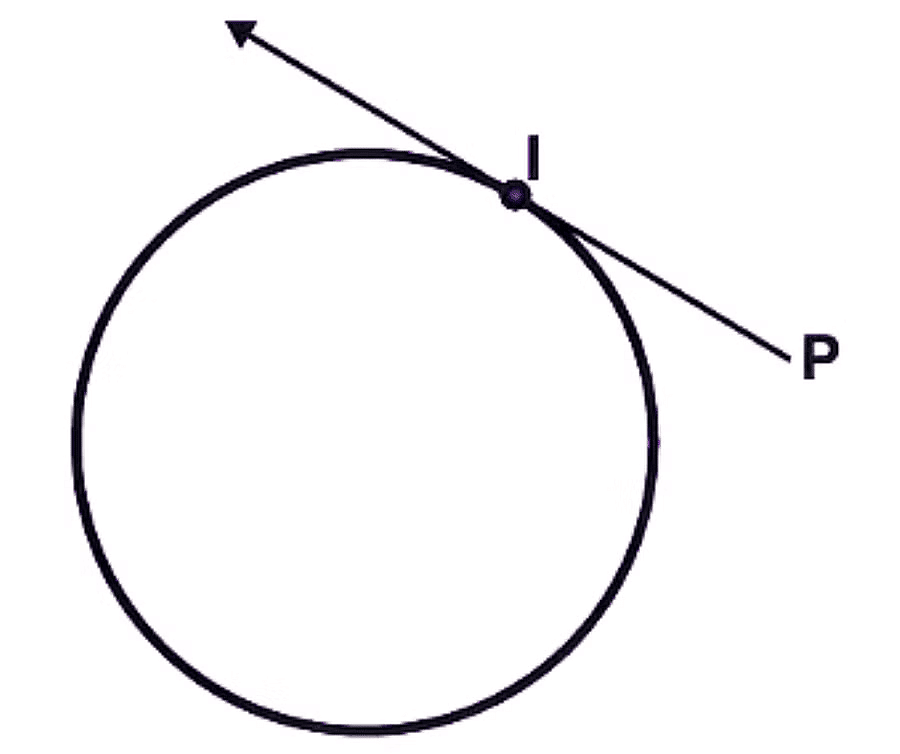
Length of a Tangent
To define the length of a tangent from a point (P) to a circle, we measure the distance from the external point P to the point of tangency "I" on the circle. This distance is known as the tangent length (PI).
Theorem 2
The lengths of tangents drawn from an external point to a circle are equal.
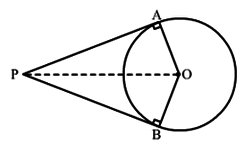
Given:
Let the circle be with center O, and P be a point outside the circle.
PQ and PR are two tangents to the circle intersecting at points Q and R respectively.
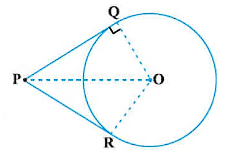
To prove:
Lengths of tangents are equal, i.e., PQ = PR.
Construction:
Join OQ, OR, and OP.
Proof:
As PQ is a tangent,
OQ ⊥ PQ
(Tangent at any point of a circle is perpendicular to the radius through the point of contact).
So, ∠OQP = 90°
Hence, ΔOQP is a right triangle.
Similarly,
PR is a tangent,
& OR ⊥ PR
(Tangent at any point of a circle is perpendicular to the radius through the point of contact).
So, ∠ORP = 90°
Hence, ΔORP is a right triangle.
Using Pythagoras theorem:
(Hypotenuse)² = (Height)² + (Base)²
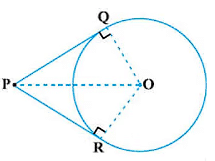
In right-angled triangle ΔOQP:
OP² = PQ² + OQ²
OP² − OQ² = PQ²
PQ² = OP² − OQ² …(1)
In right-angled triangle ΔORP:
OP² = PR² + OR²
OP² = PR² + OQ² (As OQ = OR, both are radii)
OP² − OQ² = PR²
PR² = OP² − OQ² …(2)
Note:
1. The theorem can also be proved by using the Pythagoras Theorem as follows:
PA2 = OP2 – OA2 = OP2 – OB2 = PB2 (As OA = OB) which gives PA = PB.
2. Note also that ∠ OPA = ∠ OPB. Therefore, OP is the angle bisector of ∠ APB,i.e., the centre lies on the bisector of the angle between the two tangents.
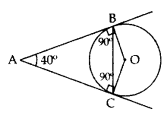
Example 2: In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then calculate ∠BOC.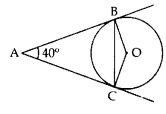
Solution:
AB and AC are tangents
∴ ∠ABO = ∠ACO = 90° (the tangent to the circle at any point is perpendicular to the radius of the circle)
In ABOC,
∠ABO + ∠ACO + ∠BAC + ∠BOC = 360° (Angle Sum Property of Quadrilateral)
90° + 90° + 40° + ∠BOC = 360°
∠BOC = 360° – 220° = 140°
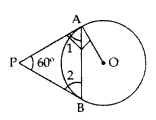
Example 3: In the given figure, PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then calculate ∠OAB.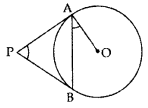
Solution:
PA = PB (The lengths of tangents drawn from an external point to a circle are equal.)
∠1 = ∠2
∠1 + ∠2 + ∠APB = 180°
∠1 + ∠1 + 60° = 180° (∠1 = ∠2)
2∠1 = 180° – 60°
2∠1 = 120°
1
∠1 = 60°
∠1 + ∠OAB = 90° (the tangent to the circle at any point is perpendicular to the radius of the circle)
60° +∠OAB = 90°
∠OAB = 90° – 60° = 30°
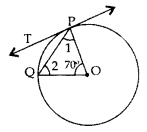
Example 4: In the given figure, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70°, then calculate ∠TPQ.
Solution:
In △POQ
∠1 = ∠2 (Isoceles triangle formed by radii of the circle)
∠1 + ∠2 + 70° = 180° (Angle Sum Property)
∠1 + ∠1 = 180° – 70° (∵∠1 = ∠2)
2∠1 = 110°
⇒ ∠1 = 55°
∠1 + ∠TPQ = 90°
55° + ∠TPQ = 90° (the tangent to the circle at any point is perpendicular to the radius of the circle)
⇒ ∠TPQ = 90° – 55° = 35°
Example 5: In the given figure, PQ R is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°. Find ∠PCA.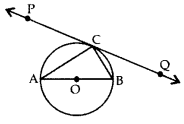
Solution:
∠ACB = 90° (Angle in the semi-circle)
In ∆ABC,
∠CAB + ∠ACB + ∠CBA = 180° (Angle Sum Property)
30 + 90° + ∠CBA = 180°
∠CBA = 180° – 30° – 90° = 60°
∠PCA = ∠CBA (Angle in the alternate segment)
∴ ∠PCA = 60°
Summary
- A circle is a two-dimensional figure formed by a set of all points equidistant from a fixed point in the same plane.
- The fixed point is called the centre of the circle, and the fixed distance from the centre is known as the radius.
- A secant is a line that intersects a circle at two distinct points.
- A tangent to a circle is a line that touches the circle at exactly one point.
- The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.
- The lengths of tangents drawn from an external point to a circle are equal.
|
127 videos|584 docs|79 tests
|
FAQs on Circles Class 10 Notes Maths Chapter 10
| 1. What is a tangent to a circle? |  |
| 2. How many tangents can be drawn from a point outside a circle? |  |
| 3. What is the relationship between the radius of the circle and the tangent? |  |
| 4. How many tangents can be drawn from a point inside a circle? |  |
| 5. What is the significance of the point of tangency in circle geometry? |  |